
Commutative ring
Encyclopedia
In ring theory
, a branch of abstract algebra
, a commutative ring is a ring
in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra
.
Some specific kinds of commutative rings are given with the following chain of class inclusions:
s, i.e. operations combining any two elements of the ring to a third. They are called addition and multiplication and commonly denoted by "+" and "⋅"; e.g. a + b and a ⋅ b. To form a ring these two operations have to satisfy a number of properties: the ring has to be an abelian group
under addition as well as a monoid
under multiplication, where multiplication distributes over addition; i.e., a ⋅ (b + c) = (a ⋅ b) + (a ⋅ c). The identity elements for addition and multiplication are denoted 0 and 1, respectively.
If, in addition, the multiplication is also commutative:
the ring R is called commutative. In the remainder of this article, all rings will be commutative, unless explicitly stated otherwise.
s Z with the two operations of addition and multiplication. As the multiplication of integers is a commutative operation, this is a commutative ring. It is usually denoted Z as an abbreviation of the German
word Zahlen (numbers).
A field
is a commutative ring where every non-zero element a is invertible; i.e., has a multiplicative inverse b such that a ⋅ b = 1. Therefore, by definition, any field is a commutative ring. The rational
, real
and complex
numbers form fields.
The ring of 2×2 matrices
is not commutative, since matrix multiplication
fails to be commutative, as the following example shows:
However, matrices that can be diagonalized
with the same similarity transformation do form a commutative ring. An example is the set of matrices of divided differences with respect to a fixed set of nodes.
If R is a given commutative ring, then the set of all polynomial
s in the variable X whose coefficients are in R forms the polynomial ring
, denoted R[X]. The same holds true for several variables.
If V is some topological space
, for example a subset of some Rn, real- or complex-valued continuous function
s on V form a commutative ring. The same is true for differentiable
or holomorphic function
s, when the two concepts are defined, such as for V a complex manifold
.
s, i.e. a non-zero element a such that there exists a non-zero element b of the ring such that ab = 0. If R possesses no zero divisors, it is called an integral domain since it closely resembles the integers in some ways.
Many of the following notions also exist for not necessarily commutative rings, but the definitions and properties are usually more complicated. For example, all ideals in a commutative ring are automatically two-sided, which simplifies the situation considerably.
s that are closed under multiplication with arbitrary ring elements and addition: for all r in R, i and j in I, both ri and i + j are required to be in I. Given any subset F = {fj}j ∈ J of R (where J is some index set), the ideal generated by F is the smallest ideal that contains F. Equivalently, it is given by finite linear combination
s
An ideal generated by one element is called principal ideal
. A ring all of whose ideals are principal is called a principal ideal ring
, two important cases are Z and k[X], the polynomial ring over a field k. Any ring has two ideals, namely the zero ideal {0} and R, the whole ring. Any ideal that is not contained in any proper ideal (i.e. ≠R) is called maximal
. An ideal m is maximal if and only if
R / m is a field. Any ring possesses at least one maximal ideal, a statement following from Zorn's lemma
, which is equivalent to the axiom of choice.
The definition of ideals is such that "dividing" I "out" gives another ring, the factor ring R / I: it is the set of coset
s of I together with the operations + (b + I) = (a + b) + I and (a + I)(b + I) = ab + I.
For example, the ring Z/nZ (also denoted Zn), where n is an integer, is the ring of integers modulo n. It is the basis of modular arithmetic
.
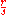 with r ∈ R, s ∈ S
with r ∈ R, s ∈ S
subject to certain rules that mimick the cancellation familiar from rational numbers. Indeed, in this language Q is the localization of Z at all nonzero integers. This construction works for any integral domain R instead of Z. The localization (R \ {0})−1R is called the quotient field of R. If S consists of the powers of one fixed element f, the localisation is written Rf.
. (Rings where it does hold are called unique factorization domain
s.) By definition, a prime ideal is a proper ideal such that, whenever the product ab of any two ring elements a and b is in p, at least one of the two elements is already in p. (The opposite conclusion holds for any ideal, by definition). Equivalently, the factor ring R / p is an integral domain. Yet another way of expressing the same is to say that the complement
R \ p is multiplicatively closed. The localisation (R \ p)−1R is important enough to have its own notation: Rp. This ring has only one maximal ideal, namely pRp. Such rings are called local
.
By the above, any maximal ideal is prime. Proving that an ideal is prime, or equivalently that a ring has no zero-divisors can be very difficult.
 Prime ideals are the key step in interpreting a ring geometrically, via the spectrum of a ring Spec R: it is the set of all prime ideals of R.This notion can be related to the spectrum of a linear operator, see Spectrum of a C*-algebra and Gelfand representation
Prime ideals are the key step in interpreting a ring geometrically, via the spectrum of a ring Spec R: it is the set of all prime ideals of R.This notion can be related to the spectrum of a linear operator, see Spectrum of a C*-algebra and Gelfand representation
. As noted above, there is at least one prime ideal, therefore the spectrum is nonempty. If R is a field, the only prime ideal is the zero ideal, therefore the spectrum is just one point. The spectrum of Z, however, contains one point for the zero ideal, and a point for any prime number p (which generates the prime ideal pZ). The spectrum is endowed with a topology called the Zariski topology
, which is determined by specifying that subsets D(f) = {p ∈ Spec R, f ∉ p}, where f is any ring element, be open. This topology tends to be different from those encountered in analysis
or differential geometry; for example, there will generally be points which are not closed. The closure
of the point corresponding to the zero ideal
0 ⊂ Z, for example, is the whole spectrum of Z.
The notion of a spectrum is the common basis of commutative algebra and algebraic geometry
. Algebraic geometry proceeds by endowing Spec R with a sheaf
 (an entity that collects functions defined locally, i.e. on varying open subsets). The datum of the space and the sheaf is called an affine scheme. Given an affine scheme, the underlying ring R can be recovered as the global sections of
(an entity that collects functions defined locally, i.e. on varying open subsets). The datum of the space and the sheaf is called an affine scheme. Given an affine scheme, the underlying ring R can be recovered as the global sections of  . Moreover, the established one-to-one correspondence between rings and affine schemes is also compatible with ring homomorphisms: any f : R → S gives rise to a continuous map in the opposite direction
. Moreover, the established one-to-one correspondence between rings and affine schemes is also compatible with ring homomorphisms: any f : R → S gives rise to a continuous map in the opposite direction
The spectrum also makes precise the intuition that localisation and factor rings are complementary: the natural maps R → Rf and R → R / fR correspond, after endowing the spectra of the rings in question with their Zariski topology, to complementary open and closed immersions respectively.
Altogether the equivalence
of the two said categories is very apt to reflect algebraic properties of rings in a geometrical manner. Affine schemes are–much the same way as manifolds are locally given by open subsets of Rn–local models for schemes
, which are the object of study in algebraic geometry. Therefore, many notions that apply to rings and homomorphisms stem from geometric intuition.
. In the case of rings, a ring homomorphism is a map f : R → S such that
These conditions ensure f(0) = 0, but the requirement that the multiplicative identity element 1 is preserved under f would not follow from the two remaining properties. In such a situation S is also called an R-algebra, by understanding that s in S may be multiplied by some r of R, by setting
The kernel and image of f are defined by ker (f) = {r ∈ R, f(r) = 0} and im (f) = f(R) = {f(r), r ∈ R}. Both kernel and image are subring
s of R and S, respectively.
over that ring, i.e., by investigating the theory of its modules
, which are similar to vector space
s, except that the base is not necessarily a field, but can be any ring R. The theory of R-modules is significantly more difficult than linear algebra of vector spaces. Module theory has to grapple with difficulties such as modules not having bases, that the rank of a free module (i.e. the analog of the dimension of vector spaces) may not be well-defined and that submodules of finitely generated modules need not be finitely generated (unless R is Noetherian, see below).
Ideals within a ring R can be characterized as R-modules which are submodules of R. On the one hand, a good understanding of R-modules necessitates enough information about R. Vice versa, however, many techniques in commutative algebra that study the structure of R, by examining its ideals, proceed by studying modules in general.
, who developed this concept) if every ascending chain of ideals
becomes stationary, i.e. becomes constant beyond some index n. Equivalently, any ideal is generated by finitely many elements, or, yet equivalent, submodules of finitely generated modules are finitely generated. A ring is called Artinian
(after Emil Artin
), if every descending chain of ideals
becomes stationary eventually. Despite the two conditions appearing symmetric, Noetherian rings are much more general than Artinian rings. For example, Z is Noetherian, since every ideal can be generated by one element, but is not Artinian, as the chain
shows. In fact, every Artinian ring is Noetherian.
Being Noetherian is an extremely important finiteness condition. The condition is preserved under many operations that occur frequently in geometry: if R is Noetherian, then so is the polynomial ring (by Hilbert's basis theorem
), any localization S−1R, factor rings R / I.
For example, a field is zero-dimensional, since the only prime ideal is the zero ideal. It is also known that a commutative ring is Artinian if and only if it is Noetherian and zero-dimensional (i.e., all its prime ideals are maximal). The integers are one-dimensional: any chain of prime ideals is of the form
since any ideal in Z is principal.
The dimension behaves well if the rings in question are Noetherian: the expected equality
holds in this case (in general, one has only dim R + 1 ≤ dim R[X] ≤ 2 · dim R + 1). Furthermore, since the dimension depends only on one maximal chain, the dimension of R is the supremum
of all dimensions of its localisations Rp, where p is an arbitrary prime ideal. Intuitively, the dimension of R is a local property of the spectrum of R. Therefore, the dimension is often considered for local rings only, also since general Noetherian rings may still be infinite, despite all their localisations being finite-dimensional.
Determining the dimension of, say,
is generally not easy. For R Noetherian, the dimension of R / I is, by Krull's principal ideal theorem
, at least dim R − n, if I is generated by n elements. If the dimension does drops as much as possible, i.e. dim R / I = dim R − n, the R / I is called a complete intersection
.
A local ring R, i.e. one with only one maximal ideal m, is called regular
, if the (Krull) dimension of R equals the dimension (as a vector space over the field R / m) of the cotangent space m / m2.
in its field of fractions
is called normal. This is a desirable property, for example any normal one-dimensional ring is necessarily regular
. Rendering a ring normal is known as normalization.
. This topology is called the I-adic topology. R can then be completed with respect to this topology. Formally, the I-adic completion is the inverse limit
of the rings R/In. For example, if k is a field, k
ring in one variable over k, is the I-adic completion of k[X] where I is the principal ideal generated by X. Analogously, the ring of p-adic integers is the I-adic completion of Z where I is the principal ideal generated by p. Any ring that is isomorphic to its own completion, is called complete.
is commutative, and therefore a finite field
. Another condition ensuring commutativity of a ring, due to Jacobson
, is the following: for every element r of R there exists an integer such that . If, r2 = r for every r, the ring is called Boolean ring
. More general conditions which guarantee commutativity of a ring are also known.
Ring theory
In abstract algebra, ring theory is the study of rings—algebraic structures in which addition and multiplication are defined and have similar properties to those familiar from the integers...
, a branch of abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, a commutative ring is a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra
Commutative algebra
Commutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
.
Some specific kinds of commutative rings are given with the following chain of class inclusions:
- Commutative rings ⊃ integral domains ⊃ integrally closed domainIntegrally closed domainIn commutative algebra, an integrally closed domain A is an integral domain whose integral closure in the field of fractions of A is A itself...
s ⊃ unique factorization domainUnique factorization domainIn mathematics, a unique factorization domain is, roughly speaking, a commutative ring in which every element, with special exceptions, can be uniquely written as a product of prime elements , analogous to the fundamental theorem of arithmetic for the integers...
s ⊃ principal ideal domainPrincipal ideal domainIn abstract algebra, a principal ideal domain, or PID, is an integral domain in which every ideal is principal, i.e., can be generated by a single element. More generally, a principal ideal ring is a nonzero commutative ring whose ideals are principal, although some authors refer to PIDs as...
s ⊃ Euclidean domainEuclidean domainIn mathematics, more specifically in abstract algebra and ring theory, a Euclidean domain is a ring that can be endowed with a certain structure – namely a Euclidean function, to be described in detail below – which allows a suitable generalization of the Euclidean algorithm...
s ⊃ fieldField (mathematics)In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
s
Definition
A ring is a set R equipped with two binary operationBinary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
s, i.e. operations combining any two elements of the ring to a third. They are called addition and multiplication and commonly denoted by "+" and "⋅"; e.g. a + b and a ⋅ b. To form a ring these two operations have to satisfy a number of properties: the ring has to be an abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
under addition as well as a monoid
Monoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
under multiplication, where multiplication distributes over addition; i.e., a ⋅ (b + c) = (a ⋅ b) + (a ⋅ c). The identity elements for addition and multiplication are denoted 0 and 1, respectively.
If, in addition, the multiplication is also commutative:
- a ⋅ b = b ⋅ a
the ring R is called commutative. In the remainder of this article, all rings will be commutative, unless explicitly stated otherwise.
First examples
An important example, and in some sense crucial, is the ring of integerInteger
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s Z with the two operations of addition and multiplication. As the multiplication of integers is a commutative operation, this is a commutative ring. It is usually denoted Z as an abbreviation of the German
German language
German is a West Germanic language, related to and classified alongside English and Dutch. With an estimated 90 – 98 million native speakers, German is one of the world's major languages and is the most widely-spoken first language in the European Union....
word Zahlen (numbers).
A field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
is a commutative ring where every non-zero element a is invertible; i.e., has a multiplicative inverse b such that a ⋅ b = 1. Therefore, by definition, any field is a commutative ring. The rational
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
, real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
and complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
numbers form fields.
The ring of 2×2 matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
is not commutative, since matrix multiplication
Matrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
fails to be commutative, as the following example shows:

However, matrices that can be diagonalized
Diagonalizable matrix
In linear algebra, a square matrix A is called diagonalizable if it is similar to a diagonal matrix, i.e., if there exists an invertible matrix P such that P −1AP is a diagonal matrix...
with the same similarity transformation do form a commutative ring. An example is the set of matrices of divided differences with respect to a fixed set of nodes.
If R is a given commutative ring, then the set of all polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s in the variable X whose coefficients are in R forms the polynomial ring
Polynomial ring
In mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
, denoted R[X]. The same holds true for several variables.
If V is some topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
, for example a subset of some Rn, real- or complex-valued continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
s on V form a commutative ring. The same is true for differentiable
Differentiable function
In calculus , a differentiable function is a function whose derivative exists at each point in its domain. The graph of a differentiable function must have a non-vertical tangent line at each point in its domain...
or holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
s, when the two concepts are defined, such as for V a complex manifold
Complex manifold
In differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....
.
Ideals and the spectrum
In contrast to fields, where every nonzero element is multiplicatively invertible, the theory of rings is more complicated. There are several notions to cope with that situation. First, an element a of a R is called a unit if it possesses a multiplicative inverse. Another particular type of element is the zero divisorZero divisor
In abstract algebra, a nonzero element a of a ring is a left zero divisor if there exists a nonzero b such that ab = 0. Similarly, a nonzero element a of a ring is a right zero divisor if there exists a nonzero c such that ca = 0. An element that is both a left and a right zero divisor is simply...
s, i.e. a non-zero element a such that there exists a non-zero element b of the ring such that ab = 0. If R possesses no zero divisors, it is called an integral domain since it closely resembles the integers in some ways.
Many of the following notions also exist for not necessarily commutative rings, but the definitions and properties are usually more complicated. For example, all ideals in a commutative ring are automatically two-sided, which simplifies the situation considerably.
Ideals and factor rings
The inner structure of a commutative ring is determined by considering its ideals, i.e. nonempty subsetSubset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
s that are closed under multiplication with arbitrary ring elements and addition: for all r in R, i and j in I, both ri and i + j are required to be in I. Given any subset F = {fj}j ∈ J of R (where J is some index set), the ideal generated by F is the smallest ideal that contains F. Equivalently, it is given by finite linear combination
Linear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
s
- r1f1 + r2f2 + ... + rnfn.
An ideal generated by one element is called principal ideal
Principal ideal
In ring theory, a branch of abstract algebra, a principal ideal is an ideal I in a ring R that is generated by a single element a of R.More specifically:...
. A ring all of whose ideals are principal is called a principal ideal ring
Principal ideal ring
In mathematics, a principal right ideal ring is a ring R in which every right ideal is of the form xR for some element x of R...
, two important cases are Z and k[X], the polynomial ring over a field k. Any ring has two ideals, namely the zero ideal {0} and R, the whole ring. Any ideal that is not contained in any proper ideal (i.e. ≠R) is called maximal
Maximal ideal
In mathematics, more specifically in ring theory, a maximal ideal is an ideal which is maximal amongst all proper ideals. In other words, I is a maximal ideal of a ring R if I is an ideal of R, I ≠ R, and whenever J is another ideal containing I as a subset, then either J = I or J = R...
. An ideal m is maximal if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
R / m is a field. Any ring possesses at least one maximal ideal, a statement following from Zorn's lemma
Zorn's lemma
Zorn's lemma, also known as the Kuratowski–Zorn lemma, is a proposition of set theory that states:Suppose a partially ordered set P has the property that every chain has an upper bound in P...
, which is equivalent to the axiom of choice.
The definition of ideals is such that "dividing" I "out" gives another ring, the factor ring R / I: it is the set of coset
Coset
In mathematics, if G is a group, and H is a subgroup of G, and g is an element of G, thenA coset is a left or right coset of some subgroup in G...
s of I together with the operations + (b + I) = (a + b) + I and (a + I)(b + I) = ab + I.
For example, the ring Z/nZ (also denoted Zn), where n is an integer, is the ring of integers modulo n. It is the basis of modular arithmetic
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
.
Localizations
The localization of a ring is the counterpart to factor rings insofar as in a factor ring R / I certain elements (namely the elements of I) become zero, whereas in the localization certain elements are rendered invertible, i.e. multiplicative inverses are added to the ring. Concretely, if S is a multiplicatively closed subset of R (i.e. whenever s, t ∈ S then so is st) then the localization of R at S, or ring of fractions with denominators in S, usually denoted S−1R consists of symbols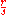 with r ∈ R, s ∈ S
with r ∈ R, s ∈ Ssubject to certain rules that mimick the cancellation familiar from rational numbers. Indeed, in this language Q is the localization of Z at all nonzero integers. This construction works for any integral domain R instead of Z. The localization (R \ {0})−1R is called the quotient field of R. If S consists of the powers of one fixed element f, the localisation is written Rf.
Prime ideals and the spectrum
A particularly important type of ideals is prime ideals, often denoted p. This notion arose when algebraists (in the 19th century) realized that, unlike in Z, in many rings there is no unique factorization into prime numbersFundamental theorem of arithmetic
In number theory, the fundamental theorem of arithmetic states that any integer greater than 1 can be written as a unique product of prime numbers...
. (Rings where it does hold are called unique factorization domain
Unique factorization domain
In mathematics, a unique factorization domain is, roughly speaking, a commutative ring in which every element, with special exceptions, can be uniquely written as a product of prime elements , analogous to the fundamental theorem of arithmetic for the integers...
s.) By definition, a prime ideal is a proper ideal such that, whenever the product ab of any two ring elements a and b is in p, at least one of the two elements is already in p. (The opposite conclusion holds for any ideal, by definition). Equivalently, the factor ring R / p is an integral domain. Yet another way of expressing the same is to say that the complement
Complement (set theory)
In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
R \ p is multiplicatively closed. The localisation (R \ p)−1R is important enough to have its own notation: Rp. This ring has only one maximal ideal, namely pRp. Such rings are called local
Local ring
In abstract algebra, more particularly in ring theory, local rings are certain rings that are comparatively simple, and serve to describe what is called "local behaviour", in the sense of functions defined on varieties or manifolds, or of algebraic number fields examined at a particular place, or...
.
By the above, any maximal ideal is prime. Proving that an ideal is prime, or equivalently that a ring has no zero-divisors can be very difficult.
Gelfand representation
In mathematics, the Gelfand representation in functional analysis has two related meanings:* a way of representing commutative Banach algebras as algebras of continuous functions;...
. As noted above, there is at least one prime ideal, therefore the spectrum is nonempty. If R is a field, the only prime ideal is the zero ideal, therefore the spectrum is just one point. The spectrum of Z, however, contains one point for the zero ideal, and a point for any prime number p (which generates the prime ideal pZ). The spectrum is endowed with a topology called the Zariski topology
Zariski topology
In algebraic geometry, the Zariski topology is a particular topology chosen for algebraic varieties that reflects the algebraic nature of their definition. It is due to Oscar Zariski and took a place of particular importance in the field around 1950...
, which is determined by specifying that subsets D(f) = {p ∈ Spec R, f ∉ p}, where f is any ring element, be open. This topology tends to be different from those encountered in analysis
Analysis
Analysis is the process of breaking a complex topic or substance into smaller parts to gain a better understanding of it. The technique has been applied in the study of mathematics and logic since before Aristotle , though analysis as a formal concept is a relatively recent development.The word is...
or differential geometry; for example, there will generally be points which are not closed. The closure
Closure (topology)
In mathematics, the closure of a subset S in a topological space consists of all points in S plus the limit points of S. Intuitively, these are all the points that are "near" S. A point which is in the closure of S is a point of closure of S...
of the point corresponding to the zero ideal
Generic point
In mathematics, in the fields general topology and particularly of algebraic geometry, a generic point P of a topological space X is an algebraic way of capturing the notion of a generic property: a generic property is a property of the generic point.- Definition and motivation :A generic point of...
0 ⊂ Z, for example, is the whole spectrum of Z.
The notion of a spectrum is the common basis of commutative algebra and algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
. Algebraic geometry proceeds by endowing Spec R with a sheaf
Sheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
 (an entity that collects functions defined locally, i.e. on varying open subsets). The datum of the space and the sheaf is called an affine scheme. Given an affine scheme, the underlying ring R can be recovered as the global sections of
(an entity that collects functions defined locally, i.e. on varying open subsets). The datum of the space and the sheaf is called an affine scheme. Given an affine scheme, the underlying ring R can be recovered as the global sections of  . Moreover, the established one-to-one correspondence between rings and affine schemes is also compatible with ring homomorphisms: any f : R → S gives rise to a continuous map in the opposite direction
. Moreover, the established one-to-one correspondence between rings and affine schemes is also compatible with ring homomorphisms: any f : R → S gives rise to a continuous map in the opposite direction
- Spec S → Spec R, q ↦ f−1(q), i.e. any prime ideal of S is mapped to its preimage under f, which is a prime ideal of R.
The spectrum also makes precise the intuition that localisation and factor rings are complementary: the natural maps R → Rf and R → R / fR correspond, after endowing the spectra of the rings in question with their Zariski topology, to complementary open and closed immersions respectively.
Altogether the equivalence
Equivalence of categories
In category theory, an abstract branch of mathematics, an equivalence of categories is a relation between two categories that establishes that these categories are "essentially the same". There are numerous examples of categorical equivalences from many areas of mathematics...
of the two said categories is very apt to reflect algebraic properties of rings in a geometrical manner. Affine schemes are–much the same way as manifolds are locally given by open subsets of Rn–local models for schemes
Scheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
, which are the object of study in algebraic geometry. Therefore, many notions that apply to rings and homomorphisms stem from geometric intuition.
Ring homomorphisms
As usual in algebra, a function f between two objects that respects the structures of the objects in question is called homomorphismHomomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
. In the case of rings, a ring homomorphism is a map f : R → S such that
- f(a + b) = f(a) + f(b), f(ab) = f(a)f(b) and f(1) = 1.
These conditions ensure f(0) = 0, but the requirement that the multiplicative identity element 1 is preserved under f would not follow from the two remaining properties. In such a situation S is also called an R-algebra, by understanding that s in S may be multiplied by some r of R, by setting
- r · s := f(r) · s.
The kernel and image of f are defined by ker (f) = {r ∈ R, f(r) = 0} and im (f) = f(R) = {f(r), r ∈ R}. Both kernel and image are subring
Subring
In mathematics, a subring of R is a subset of a ring, is itself a ring with the restrictions of the binary operations of addition and multiplication of R, and which contains the multiplicative identity of R...
s of R and S, respectively.
Modules
The outer structure of a commutative ring is determined by considering linear algebraLinear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
over that ring, i.e., by investigating the theory of its modules
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
, which are similar to vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s, except that the base is not necessarily a field, but can be any ring R. The theory of R-modules is significantly more difficult than linear algebra of vector spaces. Module theory has to grapple with difficulties such as modules not having bases, that the rank of a free module (i.e. the analog of the dimension of vector spaces) may not be well-defined and that submodules of finitely generated modules need not be finitely generated (unless R is Noetherian, see below).
Ideals within a ring R can be characterized as R-modules which are submodules of R. On the one hand, a good understanding of R-modules necessitates enough information about R. Vice versa, however, many techniques in commutative algebra that study the structure of R, by examining its ideals, proceed by studying modules in general.
Noetherian rings
A ring is called Noetherian (in honor of Emmy NoetherEmmy Noether
Amalie Emmy Noether was an influential German mathematician known for her groundbreaking contributions to abstract algebra and theoretical physics. Described by David Hilbert, Albert Einstein and others as the most important woman in the history of mathematics, she revolutionized the theories of...
, who developed this concept) if every ascending chain of ideals
Ascending chain condition
The ascending chain condition and descending chain condition are finiteness properties satisfied by some algebraic structures, most importantly, ideals in certain commutative rings...
- 0 ⊆ I0 ⊆ I1 ... ⊆ In ⊆ In + 1 ⊆ ...
becomes stationary, i.e. becomes constant beyond some index n. Equivalently, any ideal is generated by finitely many elements, or, yet equivalent, submodules of finitely generated modules are finitely generated. A ring is called Artinian
Artinian ring
In abstract algebra, an Artinian ring is a ring that satisfies the descending chain condition on ideals. They are also called Artin rings and are named after Emil Artin, who first discovered that the descending chain condition for ideals simultaneously generalizes finite rings and rings that are...
(after Emil Artin
Emil Artin
Emil Artin was an Austrian-American mathematician of Armenian descent.-Parents:Emil Artin was born in Vienna to parents Emma Maria, née Laura , a soubrette on the operetta stages of Austria and Germany, and Emil Hadochadus Maria Artin, Austrian-born of Armenian descent...
), if every descending chain of ideals
- R ⊇ I0 ⊇ I1 ... ⊇ In ⊇ In + 1 ⊇ ...
becomes stationary eventually. Despite the two conditions appearing symmetric, Noetherian rings are much more general than Artinian rings. For example, Z is Noetherian, since every ideal can be generated by one element, but is not Artinian, as the chain
- Z ⊋ 2Z ⊋ 4Z ⊋ 8Z ⊋ ...
shows. In fact, every Artinian ring is Noetherian.
Being Noetherian is an extremely important finiteness condition. The condition is preserved under many operations that occur frequently in geometry: if R is Noetherian, then so is the polynomial ring (by Hilbert's basis theorem
Hilbert's basis theorem
In mathematics, specifically commutative algebra, Hilbert's basis theorem states that every ideal in the ring of multivariate polynomials over a Noetherian ring is finitely generated. This can be translated into algebraic geometry as follows: every algebraic set over a field can be described as the...
), any localization S−1R, factor rings R / I.
Dimension
The Krull dimension (or simply dimension) dim R of a ring R is a notion to measure the "size" of a ring, very roughly by the counting independent elements in R. Precisely, it is defined as the supremum of lengths n of chains of prime ideals- 0 ⊆ p0 ⊆ p1 ⊆ ... ⊆ pn.
For example, a field is zero-dimensional, since the only prime ideal is the zero ideal. It is also known that a commutative ring is Artinian if and only if it is Noetherian and zero-dimensional (i.e., all its prime ideals are maximal). The integers are one-dimensional: any chain of prime ideals is of the form
- 0 = p0 ⊆ pZ = p1, where p is a prime numberPrime numberA prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
since any ideal in Z is principal.
The dimension behaves well if the rings in question are Noetherian: the expected equality
- dim R[X] = dim R + 1
holds in this case (in general, one has only dim R + 1 ≤ dim R[X] ≤ 2 · dim R + 1). Furthermore, since the dimension depends only on one maximal chain, the dimension of R is the supremum
Supremum
In mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
of all dimensions of its localisations Rp, where p is an arbitrary prime ideal. Intuitively, the dimension of R is a local property of the spectrum of R. Therefore, the dimension is often considered for local rings only, also since general Noetherian rings may still be infinite, despite all their localisations being finite-dimensional.
Determining the dimension of, say,
- k[X1, X2, ..., Xn] / (f1, f2, ..., fm), where k is a field and the fi are some polynomials in n variables,
is generally not easy. For R Noetherian, the dimension of R / I is, by Krull's principal ideal theorem
Krull's principal ideal theorem
In commutative algebra, Krull's principal ideal theorem, named after Wolfgang Krull , gives a bound on the height of a principal ideal in a Noetherian ring...
, at least dim R − n, if I is generated by n elements. If the dimension does drops as much as possible, i.e. dim R / I = dim R − n, the R / I is called a complete intersection
Complete intersection
In mathematics, an algebraic variety V in projective space is a complete intersection if it can be defined by the vanishing of the number of homogeneous polynomials indicated by its codimension...
.
A local ring R, i.e. one with only one maximal ideal m, is called regular
Regular local ring
In commutative algebra, a regular local ring is a Noetherian local ring having the property that the minimal number of generators of its maximal ideal is equal to its Krull dimension. In symbols, let A be a Noetherian local ring with maximal ideal m, and suppose a1, ..., an is a minimal set of...
, if the (Krull) dimension of R equals the dimension (as a vector space over the field R / m) of the cotangent space m / m2.
Constructing commutative rings
There are several ways to construct new rings out of given ones. The aim of such constructions is often to improve certain properties of the ring so as to make it more readily understandable. For example, an integral domain that is integrally closedIntegrally closed
In mathematics, more specifically in abstract algebra, the concept of integrally closed has two meanings, one for groups and one for rings. -Commutative rings:...
in its field of fractions
Field of fractions
In abstract algebra, the field of fractions or field of quotients of an integral domain is the smallest field in which it can be embedded. The elements of the field of fractions of the integral domain R have the form a/b with a and b in R and b ≠ 0...
is called normal. This is a desirable property, for example any normal one-dimensional ring is necessarily regular
Regular local ring
In commutative algebra, a regular local ring is a Noetherian local ring having the property that the minimal number of generators of its maximal ideal is equal to its Krull dimension. In symbols, let A be a Noetherian local ring with maximal ideal m, and suppose a1, ..., an is a minimal set of...
. Rendering a ring normal is known as normalization.
Completions
If I is an ideal in a commutative ring R, the powers of I form topological neighborhoods of 0 which allow R to be viewed as a topological ringTopological ring
In mathematics, a topological ring is a ring R which is also a topological space such that both the addition and the multiplication are continuous as mapswhere R × R carries the product topology.- General comments :...
. This topology is called the I-adic topology. R can then be completed with respect to this topology. Formally, the I-adic completion is the inverse limit
Inverse limit
In mathematics, the inverse limit is a construction which allows one to "glue together" several related objects, the precise manner of the gluing process being specified by morphisms between the objects...
of the rings R/In. For example, if k is a field, k
Formal power series
In mathematics, formal power series are a generalization of polynomials as formal objects, where the number of terms is allowed to be infinite; this implies giving up the possibility to substitute arbitrary values for indeterminates...
ring in one variable over k, is the I-adic completion of k[X] where I is the principal ideal generated by X. Analogously, the ring of p-adic integers is the I-adic completion of Z where I is the principal ideal generated by p. Any ring that is isomorphic to its own completion, is called complete.
Properties
By Wedderburn's theorem, every finite division ringDivision ring
In abstract algebra, a division ring, also called a skew field, is a ring in which division is possible. Specifically, it is a non-trivial ring in which every non-zero element a has a multiplicative inverse, i.e., an element x with...
is commutative, and therefore a finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
. Another condition ensuring commutativity of a ring, due to Jacobson
Nathan Jacobson
Nathan Jacobson was an American mathematician....
, is the following: for every element r of R there exists an integer such that . If, r2 = r for every r, the ring is called Boolean ring
Boolean ring
In mathematics, a Boolean ring R is a ring for which x2 = x for all x in R; that is, R consists only of idempotent elements....
. More general conditions which guarantee commutativity of a ring are also known.

