
Differential geometry of surfaces
Encyclopedia
In mathematics
, the differential geometry of surfaces deals with smooth surface
s with various additional structures, most often, a Riemannian metric.
Surfaces have been extensively studied from various perspectives: extrinsically, relating to their embedding in Euclidean space
and intrinsically, reflecting their properties determined solely by the distance within the surface as measured along curves on the surface. One of the fundamental concepts investigated is the Gaussian curvature
, first studied in depth by Carl Friedrich Gauss
(1825-1827), who showed that curvature was an intrinsic property of a surface, independent of its isometric embedding in Euclidean space.
Surfaces naturally arise as graphs of functions of a pair of variables, and sometimes appear in parametric form or as loci associated to space curves. An important role in their study has been played by Lie group
s (in the spirit of the Erlangen program
), namely the symmetry groups of the Euclidean plane, the sphere and the hyperbolic plane. These Lie groups can be used to describe surfaces of constant Gaussian curvature; they also provide an essential ingredient in the modern approach to intrinsic differential geometry through connections
. On the other hand extrinsic properties relying on an embedding of a surface in Euclidean space have also been extensively studied. This is well illustrated by the non-linear Euler-Lagrange equations in the calculus of variations
: although Euler developed the one variable equations to understand geodesics, defined independently of an embedding, one of Lagrange's main applications of the two variable equations was to minimal surfaces, a concept that can only be defined in terms of an embedding.
in the Euclidean space
, such as the boundary of a cube
, are among the first surfaces encountered in geometry. It is also possible to define smooth surfaces, in which each point has a neighborhood diffeomorphic
to some open set in E2, the Euclidean plane. This elaboration allows calculus
to be applied to surfaces to prove many results.
Two smooth surfaces are diffeomorphic if and only if they are homeomorphic. (The analogous result does not hold for higher-dimensional manifolds.) It follows that closed surfaces are classified up to diffeomorphism by their Euler characteristic
and orientability
.
Smooth surfaces equipped with Riemannian metrics are of foundational importance in differential geometry. A Riemannian metric endows a surface with notions of geodesic
, distance
, angle
, and area. An important class of such surfaces are the developable surface
s: surfaces that can be flattened to a plane An without stretching; examples include the cylinder
and the cone
.
In addition, there are properties of surfaces which depend on an embedding of the surface into Euclidean space. These surfaces are the subject of extrinsic geometry. They include
Any n-dimensional complex manifold
is, at the same time, a real (2n)-dimensional real manifold. Thus any complex one-manifold (also called a Riemann surface
) is a smooth oriented surface with an associated complex structure. Every closed surface admits complex structures. Any complex algebraic curve
or real algebraic surface
is also a smooth surface, possibly with singularities.
Complex structures on a closed oriented surface correspond to conformal equivalence classes of Riemannian metrics on the surface. One version of the uniformization theorem
(due to Poincaré
) states that any Riemannian metric on an oriented, closed surface is conformally equivalent to an essentially unique metric of constant curvature
. This provides a starting point for one of the approaches to Teichmüller theory, which provides a finer classification of Riemann surfaces than the topological one by Euler characteristic alone.
The uniformization theorem
states that every smooth Riemannian surface is conformally equivalent
is conformally equivalent
to a surface having constant curvature, and the constant may be taken to be 1, 0, or -1. A surface of constant curvature 1 is locally isometric
to the sphere, which means that every point on the surface has an open neighborhood that is isometric to an open set on the unit sphere in E3 with its intrinsic Riemannian metric. Likewise, a surface of constant curvature 0 is locally isometric to the Euclidean plane, and a surface of constant curvature -1 is locally isometric to the hyperbolic plane
.
Constant curvature surfaces are the two-dimensional realization of what are known as space form
s. These are often studied from the point of view of Felix Klein
's Erlangen programme, by means of smooth transformation groups. Any connected
surface with a three-dimensional group of isometries is a surface of constant curvature.
A complex surface is a complex two-manifold and thus a real four-manifold; it is not a surface in the sense of this article. Neither are algebraic curves or surfaces defined over fields
other than the complex numbers.
were known already to Archimedes
. The development of calculus
in the seventeenth century provided a more systematic way of proving them. Curvature of general surfaces was first studied by Euler
. In 1760 he proved a formula for the curvature of a plane section of a surface and in 1771 he considered surfaces represented in a parametric form. Monge
laid down the foundations of their theory in his classical memoir L'application de l'analyse à la géometrie which appeared in 1795. The defining contribution to the theory of surfaces was made by Gauss
in two remarkable papers written in 1825 and 1827. This marked a new departure from tradition because for the first time Gauss considered the intrinsic geometry of a surface, the properties which are determined only by the geodesic distances between points on the surface independently of the particular way in which the surface is located in the ambient Euclidean space. The crowning result, the Theorema Egregium
of Gauss, established that the Gaussian curvature
is an intrinsic invariant, i.e. invariant under local isometries
. This point of view was extended to higher-dimensional spaces by Riemann and led to what is known today as Riemannian geometry
. The nineteenth century was the golden age for the theory of surfaces, from both the topological and the differential-geometric point of view, with most leading geometers devoting themselves to their study. Darboux collected many results in his four-volume treatise Théorie des surfaces (1887–1896).
The presentation below largely follows Gauss, but with important later contributions from other geometers. For a time Gauss was Cartographer to George III of Great Britain
and Hannover; this royal patronage could explain why these papers contain practical calculations of the curvature of the earth based purely on measurements on the surface of the planet.
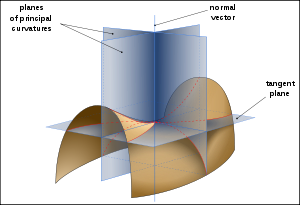
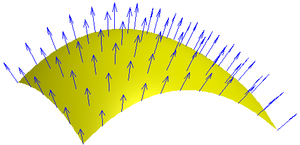 Informally Gauss defined the curvature of a surface in terms of the curvatures of certain plane curves connected with the surface. He later found a series of equivalent definitions. One of the first was in terms of the area-expanding properties of the Gauss map, a map from the surface to a 2-dimensional sphere. However, before obtaining a more intrinsic definition in terms of the area and angles of small triangles, Gauss needed to make an in-depth investigation of the properties of geodesics on the surface, i.e. paths of shortest length between two fixed points on the surface (see below).
Informally Gauss defined the curvature of a surface in terms of the curvatures of certain plane curves connected with the surface. He later found a series of equivalent definitions. One of the first was in terms of the area-expanding properties of the Gauss map, a map from the surface to a 2-dimensional sphere. However, before obtaining a more intrinsic definition in terms of the area and angles of small triangles, Gauss needed to make an in-depth investigation of the properties of geodesics on the surface, i.e. paths of shortest length between two fixed points on the surface (see below).
The Gaussian curvature at a point on an embedded smooth surface given locally by the equation
in E3, is defined to be the product of the principal curvature
s at the point;
the mean curvature is defined to be their sum. The principal curvatures are the maximum and minimum curvature
s of the plane curve
s obtained by intersecting the surface with planes normal to the tangent plane at the point. If the point is (0, 0, 0) with tangent plane z = 0, then, after a rotation about the z-axis setting the coefficient on xy to zero, F will have the Taylor series expansion
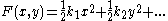
The principal curvatures are k1 and k2 in this case, the Gaussian curvature is given by
and the mean curvature by
Since K and Km are invariant under isometries
of E3, in general
and
where the derivatives at the point are given by P = Fx, Q = Fy, R = Fx x, S = Fx y, and T = Fy y.
For every oriented embedded surface the Gauss map
is the map into the unit sphere sending each point to the (outward pointing) unit normal vector to the oriented tangent plane at the point. In coordinates the map sends (x,y,z) to
Direct computation shows that

can be obtained by rotating a curve in the xz plane about the z-axis, assuming the curve does not intersect the z-axis. Suppose that the curve is given by
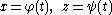
with t lies in (a, b), and is parametrized by arclength, so that
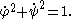
Then the surface of revolution is the point set
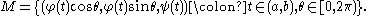
The Gaussian curvature and mean curvature are given by
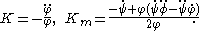
 Geodesics on a surface of revolution are governed by Clairaut's relation.
Geodesics on a surface of revolution are governed by Clairaut's relation.
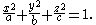
This surface admits a parametrization
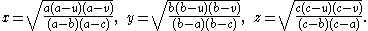
The Gaussian curvature and mean curvature are given by
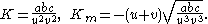

is one which can be generated by the motion of a straight line in E3. Choosing a directrix on the surface, i.e. a smooth unit speed curve c(t) orthogonal to the straight lines, and then choosing u(t) to be unit vectors along the curve in the direction of the lines, the velocity vector v=ct and u satisfy
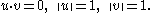
The surface consists of points
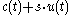
as s and t vary.
Then, if
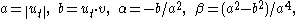
the Gaussian and mean curvature are given by
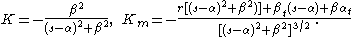
The Gaussian curvature of the ruled surface vanishes if and only if ut and v are proportional, This condition is equivalent to the surface being the envelope of the planes along the curve containing the tangent vector v and the orthogonal vector u, i.e. to the surface being developable
along the curve. More generally a surface in E3 has vanishing Gaussian curvature near a point if and only if it is developable near that point. (An equivalent condition is given below in terms of the metric.)
extended Euler's results on the calculus of variations
involving integrals in one variable to two variables. He had in mind the following problem:
Such a surface is called a minimal surface
.
In 1776 Jean Baptiste Meusnier
showed that the differential equation derived by Lagrange was equivalent to the vanishing of the mean curvature of the surface:
Minimal surfaces have a simple interpretation in real life: they are the shape a soap film will assume if a wire frame shaped like the curve is dipped into a soap solution and then carefully lifted out. The question as to whether a minimal surface with given boundary exists is called Plateau's problem
after the Belgian physicist Joseph Plateau who carried out experiments on soap films in the mid-nineteenth century. In 1930 Jesse Douglas
and Tibor Radó
gave an affirmative answer to Plateau's problem (Douglas was awarded one of the first Fields medal
s for this work in 1936).
Many explicit examples of minimal surface are known explicitly, such as the catenoid
, the helicoid
, the Scherk surface
and the Enneper surface
. There has been extensive research in this area, summarised in . In particular a result of Osserman shows that if a minimal surface is non-planar, then its image under the Gauss map is dense in S2.
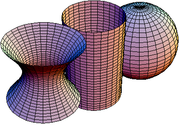
Each of these surfaces of constant curvature has a transitive Lie group
of symmetries. This group theoretic fact has far-reaching consequences, all the more remarkable because of the central role these special surfaces play in the geometry of surfaces, due to Poincaré
's uniformization theorem
(see below).
Other examples of surfaces with Gaussian curvature 0 include cones
, tangent developable
s, and more generally any developable surface.
 For any surface embedded in Euclidean space of dimension 3 or higher, it is possible to measure the length of a curve on the surface, the angle between two curves and the area of a region on the surface. This structure is encoded infinitesimally in a Riemannian metric on the surface through line elements and area elements. Classically in the nineteenth and early twentieth centuries only surfaces embedded in R3 were considered and the metric was given as a 2 x 2 positive definite matrix varying smoothly from point to point in a local parametrization of the surface. The idea of local parametrization and change of coordinate was later formalized through the current abstract notion of a manifold
For any surface embedded in Euclidean space of dimension 3 or higher, it is possible to measure the length of a curve on the surface, the angle between two curves and the area of a region on the surface. This structure is encoded infinitesimally in a Riemannian metric on the surface through line elements and area elements. Classically in the nineteenth and early twentieth centuries only surfaces embedded in R3 were considered and the metric was given as a 2 x 2 positive definite matrix varying smoothly from point to point in a local parametrization of the surface. The idea of local parametrization and change of coordinate was later formalized through the current abstract notion of a manifold
, a topological space where the smooth structure
is given by local charts on the manifold, exactly as the planet Earth
is mapped by atlas
es today. Changes of coordinates between different charts of the same region are required to be smooth. Just as contour lines on real-life maps encode changes in elevation, taking into account local distortions of the Earth's surface to calculate true distances, so the Riemannian metric describes distances and areas "in the small" in each local chart. In each local chart a Riemannian metric is given by smoothly assigning a 2 x 2 positive definite matrix to each point; when a different chart is taken, the matrix is transformed according to the Jacobian matrix of the coordinate change. The manifold then has the structure of a 2-dimensional Riemannian manifold
.
and
The expression E dx2 + 2F dx dy + G dy2 is called the first fundamental form.
The matrix
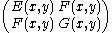
is required to be positive-definite
and to depend smoothly on x and y.
In a similar way line and area elements can be associated to any abstract Riemannian 2-manifold
in a local chart.
in the ambient Euclidean space, i.e. there is an isometry
of E3 carrying one surface onto the other. With this more rigid definition of similitude, the cylinder and the plane are obviously no longer the same.
Although the primary invariant in the study of the intrinsic geometry of surfaces is the metric (the first fundamental form) and the Gaussian curvature, certain properties of surfaces also depend on an embedding into E3 (or a higher dimensional Euclidean space). The most important example is the second fundamental form, defined classically as follows.
Take a point (x, y) on the surface in a local chart. The square of the Euclidean distance from a nearby point (x + dx, y + dy) to the tangent plane at (x, y), i.e. the square of the length of the perpendicular dropped from the nearby point to the tangent plane, has the form
plus third and higher order corrections. The above expression, a symmetric bilinear form at each point, is the second fundamental form.
It is described by a 2 × 2 symmetric matrix
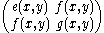
which depends smoothly on x and y. The Gaussian curvature can be calculated as the ratio of the determinants of the second and first fundamental forms:
Remarkably Gauss proved that it is an intrinsic invariant (see his Theorema Egregium below).
One of the other extrinisic numerical invariants of a surface is the mean curvature
Km, defined as the sum of the principal curvatures. It is given by the formula
The coefficients of the first and second fundamental forms satisfy certain compatibility conditions known as the Gauss-Codazzi equations;
they involve the Christoffel symbols
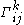 associated with the first fundamental form:
associated with the first fundamental form:
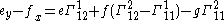
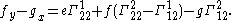
These equations can also be succinctly expressed and derived in the language of connection form
s due to Élie Cartan
. Pierre Bonnet
proved that two quadratic forms satisfying the Gauss-Codazzi equations always uniquely determine an embedded surface locally. For this reason the Gauss-Codazzi equations are often called the fundamental equations for embedded surfaces, precisely identifying where the intrinsic and extrinsic curvatures come from. They admit generalizations to surfaces embedded in more general Riemannian manifold
s.
df of the Gauss map f can be used to define a type of extrinsic curvature, known as the shape operator or Weingarten map. This operator first appeared implicitly in the work of Wilhelm Blaschke
and later explicitly in a treatise by Burali-Forti and Burgati.
Since at each point x of the surface, the tangent space is an inner product space, the shape operator Sx can be defined as a linear operator on this space by the formula
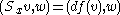
for tangent vectors v, w (the inner product makes sense because df(v) and w both lie in E3). The right hand side is symmetric in v and w, so the shape operator is self-adjoint on the tangent space. The eigenvalues of Sx are just the principal curvatures k1 and k2 at x. In particular the determinant
of the shape operator at a point is the Gaussian curvature, but it also contains other information, since the mean curvature
is half the trace
of the shape operator. The mean curvature is an extrinsic invariant. In intrinsic geometry, a cylinder is developable, meaning that every piece of it is intrinsically indistinguishable from a piece of a plane since its Gauss curvature vanishes identically. Its mean curvature is not zero, though; hence extrinsically it is different from a plane.
In general, the eigenvectors and eigenvalues
of the shape operator at each point determine the directions in which the surface bends at each point. The eigenvalues correspond to the principal curvatures of the surface and the eigenvectors are the corresponding principal directions. The principal directions specify the directions that a curve embedded in the surface must travel to have maximum and minimum curvature, these being given by the principal curvatures.
The shape operator is given in terms of the components of the first and second fundamental forms by the Weingarten equations
:
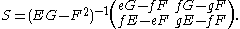
s; they are the shape that an elastic band stretched between the two points would take. Mathematically they are described using partial differential equation
s from the calculus of variations
. The differential geometry of surfaces revolves around the study of geodesics. It is still an open question whether every Riemannian metric on a 2-dimensional local chart arises from an embedding in 3-dimensional Euclidean space: the theory of geodesics has been used to show this is true in the important case when the components of the metric are analytic
.
 Given a piecewise smooth path c(t) = (x(t), y(t)) in the chart for t in [a, b], its length is defined by
Given a piecewise smooth path c(t) = (x(t), y(t)) in the chart for t in [a, b], its length is defined by
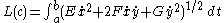
and energy by
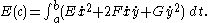
The length is independent of the parametrisation of a path. By the Euler-Lagrange equations, if c(t) is a path minimising length, parametrised by arclength, it must satisfy the Euler equations
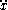 + Γ¹11
+ Γ¹11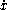 ² + 2Γ¹12
² + 2Γ¹12 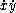 + Γ¹22
+ Γ¹22 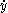 ² =0 and
² =0 and 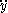 + Γ²11
+ Γ²11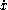 ² + 2Γ²12
² + 2Γ²12 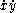 + Γ²22
+ Γ²22 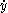 ² =0
² =0
where the Christoffel symbols
Γkij are given by
where g11 = E, g12=F, g22 =G and (gij) is the inverse matrix to (gij). A path satisfying the Euler equations is called a geodesic
.
By the Cauchy-Schwarz inequality a path minimising energy is just a geodesic parametrised by arc length; and, for any geodesic, the parameter t is proportional to arclength.
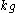 at a point of a curve c(t), parametrised by arc length, on an oriented surface is defined to be
at a point of a curve c(t), parametrised by arc length, on an oriented surface is defined to be
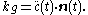
where n(t) is the "principal" unit normal to the curve in the surface, constructed by rotating the unit tangent vector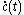 through an angle of + 90°.
through an angle of + 90°.
The geodesic curvature measures in a precise way how far a curve on the surface is from being a geodesic.
Apart from some special cases, whether this is possible in E3 remains an open question, the so-called "Weyl problem". In 1926 Maurice Janet proved that it is always possible locally if E, F and G are analytic
; soon afterwards Élie Cartan
generalised this to local embeddings of Riemannian n-manifolds
in Em where m = ½(n² +n). To prove Janet's theorem near (0,0), the Cauchy-Kowalevski theorem is used twice to produce analytic geodesics orthogonal to the y-axis and then the x-axis to make an analytic change of coordinate so that E=1 and F=0. An isometric embedding u must satisfy
Differentiating gives the three additional equations
with u(0,y) and ux(0,y) prescribed. These equations can be solved near (0,0) using the Cauchy-Kowalevski theorem and yield a solution
of the original embedding equations.
. If H=(EG)½, then the Gaussian curvature is given by
If in addition E=1, so that H=G½, then the angle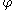 at the intersection between geodesic (x(t),y(t)) and the line y = constant is given by the equation
at the intersection between geodesic (x(t),y(t)) and the line y = constant is given by the equation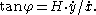
The derivative of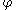 is given by a classical derivative formula of Gauss:
is given by a classical derivative formula of Gauss:
and its generalisations. Roughly speaking this lemma states that geodesics starting at the base point must cut the spheres of fixed radius centred on the base point at right angles. Geodesic polar coordinates are obtained by combining the exponential map with polar coordinates on tangent vectors at the base point.
The Gaussian curvature of the surface is then given by the second order deviation of the metric at the point from the Euclidean metric. In particular the Gaussian curvature is an invariant of the metric, Gauss's celebrated Theorema Egregium
. A convenient way to understand the curvature comes from an ordinary differential equation, first considered by Gauss and later generalized by Jacobi, arising from the change of normal coordinates about two different points. The Gauss–Jacobi equation provides another way of computing the Gaussian curvature. Geometrically it explains what happens to geodesics from a fixed base point as the endpoint varies along a small curve segment through data recorded in the Jacobi field
, a vector field
along the geodesic. One and a quarter centuries after Gauss and Jacobi, Marston Morse
gave a more conceptual interpretation of the Jacobi field in terms of second derivatives of the energy function on the infinite-dimensional Hilbert manifold
of paths.
s shows that if f(t, v) is smooth then the differential equation
dv/dt = f(t,v) with initial condition v(0) = v0 has a unique solution for |t| sufficiently small and the solution depends smoothly
on t and v0. This implies that for sufficiently small tangent vector
s v at a given point p = (x0,y0), there is a geodesic cv(t) defined on (−2,2) with cv(0) = (x0,y0) and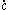 v(0) = v. Moreover if |s| ≤ 1, then csv = cv(st). The exponential map is defined by
v(0) = v. Moreover if |s| ≤ 1, then csv = cv(st). The exponential map is defined by
and gives a diffeomorphism between a disc ||v|| < δ and a neighbourhood of p; more generally the map sending (p,v) to expp(v) gives a local diffeomorphism onto a neighbourhood of (p,p). The exponential map gives geodesic normal coordinates near p.
where L, M are quadratic and λ, μ cubic homogeneous polynomials in u and v. If u and v are fixed, x(t) = x(tu,tv) and y(t) = y(tu, tv) can be considered as formal power series solutions of the Euler equations: this uniquely determines α, β, L, M, λ and μ.
a key result, usually called the Gauss lemma
. Geometrically it states that
Taking polar coordinates (r,θ), it follows that the metric has the form
In geodesic coordinates, it is easy to check that the geodesics through zero minimize length. The topology on the Riemannian manifold is then given by a distance function d(p,q), namely the infimum
of the lengths of piecewise smooth paths between p and q. This distance is realised locally by geodesics,
so that in normal coordinates d(0,v) = ||v||. If the radius δ is taken small enough, a slight sharpening of the Gauss lemma shows that the image U of the
disc ||v|| < δ under the exponential map is geodesically convex, i.e. any two points in U are joined by a unique geodesic lying entirely inside U.
k1 x2 + k2 y2 + ···, the power series expansion of the metric is given in normal coordinates (u, v) as
This extraordinary result — Gauss' Theorema Egregium
— shows that the Gaussian curvature of a surface can be computed solely in terms of the metric
and is thus an intrinsic invariant of the surface, independent of any embedding in E³ and unchanged under coordinate transformations. In particular isometries of surfaces preserve Gaussian curvature.
by Jacobi
,
The Jacobian of this coordinate change at q is equal to Hr. This gives another way of establishing the intrinsic nature of Gaussian curvature. Because H(r,θ) can be interpreted as the length of the line element in the θ direction, the Gauss–Jacobi equation shows that the Gaussian curvature measures the spreading of geodesics on a geometric surface as they move away from a point.
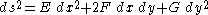
and Laplace–Beltrami operator
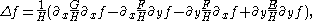
where H2 = EG – F 2, the Gaussian curvature at a point is given by the formula
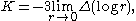
where r is the denotes the geodesic distance from the point.
Since Δ is manifestly an intrinsic invariant, this gives yet another proof that the Gaussian curvature is an intrinsic invariant.
In isothermal coordinates
, first considered by Gauss, the metric is required to be of the special form
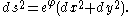
In this case the Laplace–Beltrami operator is given by
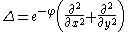
and φ satisfies Liouville's equation
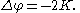
Isothermal coordinates are known to exist in a neighbourhood of any point on the surface, although all proofs to date rely on non-trivial results on partial differential equation
s. There is an elementary proof for minimal surfaces.
 On a sphere
On a sphere
or a hyperboloid, the area of a geodesic triangle, i.e. a triangle all the sides of which are geodesics, is proportional to the difference of the sum of the interior angles and π. The constant of proportionality is just the Gaussian curvature, a constant for these surfaces. For the torus, the difference is zero, reflecting the fact that its Gaussian curvature is zero. These are standard results in spherical, hyperbolic and high school trigonometry (see below). Gauss generalised these results to an arbitrary surface by showing that the integral of the Gaussian curvature over the interior of a geodesic triangle is also equal to this angle difference or excess. His formula showed that the Gaussian curvature could be calculated near a point as the limit of area over angle excess for geodesic triangles shrinking to the point. Since any closed surface can be decomposed up into geodesic triangles, the formula could also be used to compute the integral of the curvature over the whole surface. As a special case of what is now called the Gauss-Bonnet theorem, Gauss proved that this integral was remarkably always 2π times an integer, a topological invariant of the surface called the Euler characteristic
. This invariant is easy to compute combinatorially in terms of the number of vertices, edges, and faces of the triangles in the decomposition, also called a triangulation
. This interaction between analysis and topology was the forerunner of many later results in geometry, culminating in the Atiyah-Singer index theorem. In particular properties of the curvature impose restrictions on the topology of the surface.
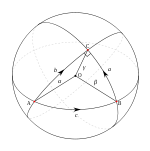
In fact taking geodesic polar coordinates with origin A and AB, AC the radii at polar angles 0 and α
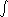 Δ K dA =
Δ K dA =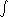 Δ KH dr dθ = –
Δ KH dr dθ = – 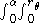 Hrr dr dθ =
Hrr dr dθ = 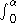 1 − Hr(rθ,θ) dθ =
1 − Hr(rθ,θ) dθ = 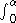 dθ +
dθ + 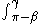 dφ = α + β + γ − π,
dφ = α + β + γ − π,
where the second equality follows from the Gauss–Jacobi equation and the fourth from Gauss' derivative formula in the orthogonal coordinates (r,θ).
Gauss' formula shows that the curvature at a point can be calculated as the limit of angle excess α + β + γ − π over area for successively smaller geodesic triangles near the point. Qualitatively a surface is positively or negatively curved according to the sign of the angle excess for arbitrarily small geodesic triangles.

Since every compact oriented 2-manifold M can be triangulated
by small geodesic triangles, it follows that
where χ(M) denotes the Euler characteristic
of the surface.
In fact if there are F faces, E edges and V vertices, then 3F = 2E and the left hand side equals 2π·V – π·F = 2π·(V – E + F) = 2π·χ(M).
This is the celebrated Gauss-Bonnet theorem: it shows that the integral of the Gaussian curvature is a topological invariant of the manifold, namely the Euler characteristic. This theorem can be interpreted in many ways; perhaps one of the most far-reaching has been as the index theorem for an elliptic differential operator on M, one of the simplest cases of the Atiyah-Singer index theorem. Another related result, which can be proved using the Gauss-Bonnet theorem, is the Poincaré-Hopf index theorem for vector fields on M which vanish at only a finite number of points: the sum of the indices
at these points equals the Euler characteristic. (On a small circle round each isolated zero, the vector field defines a map into the unit circle; the index is just the winding number
of this map.)
observed, in this case the surface is convex
; this criterion for convexity can be viewed as a 2-dimensional generalisation of the well-known second derivative criterion for convexity of plane curves. Hilbert
proved that every isometrically embedded closed surface must have a point of positive curvature. Thus a closed Riemannian 2-manifold of non-positive curvature can never be embedded isometrically in E3; however, as Adriano Garsia
showed using the Beltrami equation for quasiconformal mapping
s, this is always possible for some conformally equivalent
metric.
. Each of these has a transitive three-dimensional Lie group
of orientation preserving isometries
G, which can be used to study their geometry. Each of the two non-compact surfaces can be identified with the quotient G / K where K is a maximal compact subgroup
of G. Here K is isomorphic to SO(2). Any other closed Riemannian 2-manifold M of constant Gaussian curvature, after scaling the metric by a constant factor if necessary, will have one of these three surfaces as its universal covering space. In the orientable case, the fundamental group
Γ of M can be identified with a torsion-free
uniform subgroup
of G and M can then be identified with the double coset space
Γ \ G / K. In the case of the sphere and the Euclidean plane, the only possible examples are the sphere itself and tori obtained as quotients of R2 by discrete rank 2 subgroups. For closed surfaces of genus
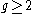 , the moduli space
, the moduli space
of Riemann surfaces obtained as Γ varies over all such subgroups, has real dimension 6g - 6 . By Poincaré's uniformization theorem
, any orientable closed 2-manifold is conformally equivalent
to a surface of constant curvature 0, +1 or –1. In other words, by multiplying the metric by a positive scaling factor, the Gaussian curvature can be made to take exactly one of these values (the sign of the Euler characteristic
of M).
 In the case of the Euclidean plane, the symmetry group is the Euclidean motion group
In the case of the Euclidean plane, the symmetry group is the Euclidean motion group
, the semidirect product
of
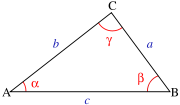
the two dimensional group of translations by the group of rotations. Geodesics are straight lines and the geometry is encoded in the elementary formulas of trigonometry
, such as the cosine rule for a triangle with sides a, b, c and angles α, β, γ:
Flat tori can be obtained by taking the quotient of R2 by a lattice, i.e. a free Abelian subgroup of rank 2. These closed surfaces have no isometric embeddings in E3. They do nevertheless admit isometric embeddings in E4; in the easiest case this follows from the fact that the torus is a product of two circles and each circle can be isometrically embedded in E2.
 The isometry group of the unit sphere S2 in E3 is the orthogonal group O(3), with the rotation group
The isometry group of the unit sphere S2 in E3 is the orthogonal group O(3), with the rotation group
SO(3) as the subgroup of isometries preserving orientation. It is the direct product of SO(3) with the antipodal map, sending x to –x. The group SO(3) acts transitively on S2. The stabilizer subgroup of the unit vector (0,0,1) can be identified with SO(2), so that S2 = SO(3)/SO(2).
The geodesics between two points on the sphere are the great circle
arcs with these given endpoints. If the points are not antipodal, there is a unique shortest geodesic between the points. The geodesics can also be described group theoretically: each geodesic through the North pole (0,0,1) is the orbit of the subgroup of rotations about an axis through antipodal points on the equator.
A spherical triangle is a geodesic triangle on the sphere. It is defined by points A, B, C on the sphere with sides BC, CA, AB formed from great circle arcs of length less than π. If the lengths of the sides are a, b, c and the angles between the sides α, β, γ,
then the spherical cosine law states that
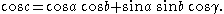
The area of the triangle is given by
Using stereographic projection
from the North pole, the sphere can be identified with the extended complex plane C {∞}. The explicit map is given by
{∞}. The explicit map is given by
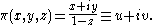
Under this correspondence every rotation of S2 corresponds to a Möbius transformation in SU(2), unique up to sign. With respect to the coordinates (u, v) in the complex plane, the spherical metric becomes
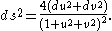
The unit sphere is the unique closed orientable surface with constant curvature +1. The quotient SO(3)/O(2) can be identified with the real projective plane
. It is non-orientable and can be described as the quotient of S2 by the antipodal map (multiplication by –1). The sphere is simply connected, while the real projective plane has fundamental group Z2. The finite subgroups of SO(3)
, corresponding to the finite subgroups of O(2) and the symmetry groups of the platonic solids, do not act freely on S2, so the corresponding quotients are not 2-manifolds, just orbifold
s.


 Non-Euclidean geometry
Non-Euclidean geometry
was first discussed in letters of Gauss, who made extensive computations at the turn of the nineteenth century which, although privately circulated, he decided not to put into print. In 1830 Lobachevsky and independently in 1832 Bolyai, the son of one Gauss' correspondents, published synthetic versions of this new geometry, for which they were severely criticized. However it was not until 1868 that Beltrami
, followed by Klein
in 1871 and Poincaré
in 1882, gave concrete analytic models for what Klein dubbed hyperbolic geometry
. The four models of 2-dimensional hyperbolic geometry that emerged were:
The first model, based on a disk, has the advantage that geodesics are actually line segments (that is, intersections of Euclidean lines with the open unit disk).The last model has the advantage that it gives a construction which is completely parallel to that of the unit sphere in 3-dimensional Euclidean space. Because of their application in complex analysis and geometry, however, the models of Poincaré are the most widely used: they are interchangeable thanks to the Möbius transformations between the disk and the upper half-plane.
Let
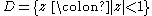
be the Poincaré disk in the complex plane with Poincaré metric
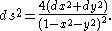
In polar coordinates (r, θ) the metric is given by
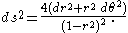
The length of a curve γ:[a,b]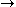 D is given by the formula
D is given by the formula
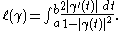
The group G = SU(1,1) given by
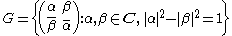
acts transitively by Möbius transformations on D and the stabilizer subgroup of 0 is the rotation group
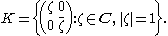
The quotient group SU(1,1)/±I is the group of orientation-preserving isometries of D. Any two points z, w in D are joined by a unique geodesic, given by the portion of the circle or straight line passing through z and w and orthogonal to the boundary circle. The distance between z and w is given by
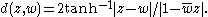
In particular d(0,r) = 2 tanh−1 r and c(t) = tanh t/2 is the geodesic through 0 along the real axis, parametrized by arclength.
The topology defined by this metric is equivalent to the usual Euclidean topology, although as a metric space (D,d) is complete.
A hyperbolic triangle
is a geodesic triangle for this metric: any three points in D are vertices of a hyperbolic triangle. If the sides have length a, b, c with corresponding angles α, β, γ, then the hyperbolic cosine rule states that
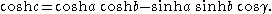
The area of the hyperbolic triangle is given by
The unit disk and the upper half-plane
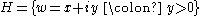
are conformally equivalent by the Möbius transformations
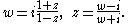
Under this correspondence the action of SL(2,R) by Möbius transformations on H corresponds to that of SU(1,1) on D. The metric on H becomes
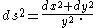
Since lines or circles are preserved under Möbius transformations, geodesics are again described by lines or circles orthogonal to the real axis.
The unit disk with the Poincaré metric is the unique simply connected oriented 2-dimensional Riemannian manifold with constant curvature -1. Any oriented closed surface M with this property has D as its universal covering space. Its fundamental group
can be identified with a torsion-free
concompact subgroup Γ of SU(1,1), in such a way that
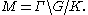
In this case Γ is a finitely presented group. The generators and relations are encoded in a geodesically convex fundamental geodesic polygon in D (or H) corresponding geometrically to closed geodesics on M.
Examples.
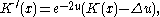
where Δ is the Laplacian for the original metric. Thus to show that a given surface is conformally equivalent to a metric with constant curvature K
it suffices to solve the following variant of Liouville's equation:
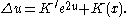
When M has Euler characteristic 0, so is diffeomorphic to a torus
, K = 0, so this amounts to solving
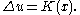
By standard elliptic theory, this is possible because the integral of K over M is zero, by the Gauss-Bonnet theorem.
When M has negative Euler characteristic, K = -1, so the equation to be solved is:
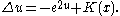
Using the continuity of the exponential map on Sobolev space
due to Neil Trudinger
, this non-linear equation can always be solved.
Finally in the case of the 2-sphere, K = 1 and the equation becomes:
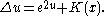
So far this non-linear equation has not been analysed directly, although classical results such as the Riemann-Roch theorem imply that it always has a solution. The method of Ricci flow
, developed by Richard Hamilton
, gives another proof of existence based on non-linear partial differential equations to prove existence. In fact the Ricci flow on conformal metrics on S2 is defined on functions u(x, t) by
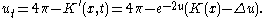
After finite time, Chow showed that K' becomes positive; previous results of Hamilton could then be used to show that K' converges to +1.
A simple proof using only elliptic operators discovered in 1988 can be found in . Let G be the Green's function
on
S2 satisfying ΔG = 1 + 4πδP, where δP is the point measure at a fixed point P of S2. The equation Δv = 2K – 2, has a smooth solution v, because the right hand side has integral 0 by the Gauss-Bonnet theorem. Thus φ = 2G + v satisfies Δφ = 2K away from P. It follows that g1 = eφg is a complete metric of constant curvature 0 on the complement of P, which is therefore isometric to the plane. Composing with stereographic projection
, it follows that there is a smooth function u such that e2ug has Gaussian curvature +1 on the complement of P. The function u automatically extends to a smooth function on the whole of S2.
inequalities of comparison geometry, studied by Cartan
, Alexandrov
and Toponogov
, and considered later from a different point of view by Bruhat
and Tits
; thanks to the vision of Gromov, this characterisation of non-positive curvature in terms of the underlying metric space has had a profound impact on modern geometry and in particular geometric group theory
. Many results known for smooth surfaces and their geodesics, such as Birkhoff's method of constructing geodesics by his curve-shortening process or van Mangoldt and Hadamard's theorem that a simply connected surface of non-positive curvature is homeomorphic to the plane, are equally valid in this more general setting.
The inequality follows from the fact that if c(t) describes a geodesic parametrised by arclength and a is a fixed point, then
is a convex function
, i.e.
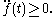
Taking geodesic polar coordinates with origin at a so that ||c(t)|| = r(t), convexity is equivalent to
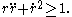
Changing to normal coordinates u, v at c(t), this inequality becomes
where (u,v) corresponds to the unit vector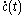 .
.
This follows from the inequality Hr ≥ H, a consequence of the non-negativity of the derivative of the Wronskian
of H and r from Sturm–Liouville theory.

applies in higher dimensions. The completeness assumption is automatically fulfilled for a surface which is embedded as a closed subset of Euclidean space.
However, it is no longer fulfilled if, for example, we remove an isolated point from a surface. For example, the complement of the origin in the Euclidean plane
is an example of a non-complete surface; in this example two points which are diametrically opposite across the origin cannot be
joined by a geodesic without leaving the punctured plan).
(1881) and Hadamard
(1898) proved that the exponential map at a point is a covering map, so that the universal covering space of the manifold is E². This result was generalised to higher dimensions by Cartan
and is usually referred to in this form as the Cartan–Hadamard theorem
. For surfaces, this result follows from three important facts:
 The classical approach of Gauss to the differential geometry of surfaces was the standard elementary approach which predated the emergence of the concepts of Riemannian manifold
The classical approach of Gauss to the differential geometry of surfaces was the standard elementary approach which predated the emergence of the concepts of Riemannian manifold
initiated by Bernhard Riemann
in the mid-nineteenth century and of connection
developed by Tullio Levi-Civita
, Élie Cartan
and Hermann Weyl
in the early twentieth century. The notion of connection, covariant derivative
and parallel transport
gave a more conceptual and uniform way of understanding curvature, which not only allowed generalisations to higher dimensional manifolds but also provided an important tool for defining new geometric invariants, called characteristic classes. The approach using covariant derivatives and connections is nowadays the one adopted in more advanced textbooks.
is perhaps most easily understood in terms of lifting vector field
s, considered as first order differential operator
s acting on functions on the manifold, to differential operators on the tangent bundle
or frame bundle
.
In the case of an embedded surface, the lift to an operator on vector fields, called the covariant derivative, is very simply described in terms of orthogonal projection. Indeed a vector field on a surface embedded in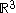 can be regarded as a function from the surface into R3. Another vector field act as a differential operator component-wise. The resulting vector field will not be tangent to the surface, but this can be corrected taking its orthogonal projection onto the tangent space at each point of the surface. As Ricci
can be regarded as a function from the surface into R3. Another vector field act as a differential operator component-wise. The resulting vector field will not be tangent to the surface, but this can be corrected taking its orthogonal projection onto the tangent space at each point of the surface. As Ricci
and Levi-Civita realised at the turn of the twentieth century, this process depends only on the metric and can be locally expressed in terms of the Christoffel symbols.
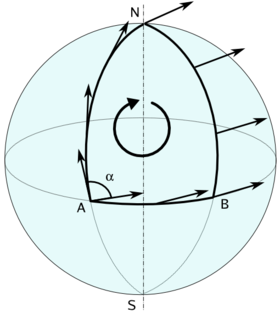
of tangent vectors along a curve in the surface was the next major advance in the subject, due to Levi-Civita. It is related to the earlier notion of covariant derivative, because it is the monodromy
of the ordinary differential equation
on the curve defined by the covariant derivative with respect to the velocity vector of the curve. Parallel transport along geodesics, the "straight lines" of the surface, can also easily be described directly. A vector in the tangent plane is transported along a geodesic as the unique vector field with constant length and making a constant angle with the velocity vector of the geodesic. For a general curve, this process has to be modified using the geodesic curvature, which measures how far the curve departs from being a geodesic.
A vector field v(t) along a unit speed curve c(t), with geodesic curvature kg(t), is said to be parallel along the curve if
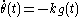
This recaptures the rule for parallel transport along a geodesic or piecewise geodesic curve, because in that case kg = 0, so that the angle θ(t) should remain constant on any geodesic segment. The existence of parallel transport follows because θ(t) can be computed as the integral
of the geodesic curvature. Since it therefore depends continuously on the L2 norm of kg, it follows that parallel transport for an arbitrary curve can be obtained as the limit of the parallel transport on approximating piecewise geodesic curves.
The connection can thus be described in terms of lifting paths in the manifold to paths in the tangent or orthonormal frame bundle, thus formalising the classical theory of the "moving frame
", favoured by French authors. Lifts of loops about a point give rise to the holonomy group at that point. The Gaussian curvature at a point can be recovered from parallel transport around increasingly small loops at the point. Equivalently curvature can be calculated directly at an infinitesimal level in terms of Lie brackets
of lifted vector fields.

of M, gives a third way to understand the Riemannian connection.
They noticed that parallel transport dictates that a path in the surface be lifted to a path in the frame bundle so that its tangent vectors lie in a
special subspace of codimension one in the three-dimensional tangent space of the frame bundle. The projection onto this subspace is defined by a differential 1-form on the orthonormal frame bundle, the connection form
. This enabled the curvature properties of the surface to be encoded in differential forms on the frame bundle and formulas involving their exterior derivative
s.
This approach is particularly simple for an embedded surface. Thanks to a result of , the connection 1-form on a surface embedded in Euclidean space E3 is just the pullback under the Gauss map of the connection 1-form on S2. Using the identification of S2 with the homogeneous space
SO(3)/SO(2), the connection 1-form is just a component of the Maurer-Cartan 1-form
on SO(3).
, the von Mangoldt-Hadamard theorem, and the embeddability theorem. There are other important aspects of the global geometry of surfaces. These include:

can be found in , and .
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the differential geometry of surfaces deals with smooth surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
s with various additional structures, most often, a Riemannian metric.
Surfaces have been extensively studied from various perspectives: extrinsically, relating to their embedding in Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
and intrinsically, reflecting their properties determined solely by the distance within the surface as measured along curves on the surface. One of the fundamental concepts investigated is the Gaussian curvature
Gaussian curvature
In differential geometry, the Gaussian curvature or Gauss curvature of a point on a surface is the product of the principal curvatures, κ1 and κ2, of the given point. It is an intrinsic measure of curvature, i.e., its value depends only on how distances are measured on the surface, not on the way...
, first studied in depth by Carl Friedrich Gauss
Carl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
(1825-1827), who showed that curvature was an intrinsic property of a surface, independent of its isometric embedding in Euclidean space.
Surfaces naturally arise as graphs of functions of a pair of variables, and sometimes appear in parametric form or as loci associated to space curves. An important role in their study has been played by Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s (in the spirit of the Erlangen program
Erlangen program
An influential research program and manifesto was published in 1872 by Felix Klein, under the title Vergleichende Betrachtungen über neuere geometrische Forschungen...
), namely the symmetry groups of the Euclidean plane, the sphere and the hyperbolic plane. These Lie groups can be used to describe surfaces of constant Gaussian curvature; they also provide an essential ingredient in the modern approach to intrinsic differential geometry through connections
Connection (mathematics)
In geometry, the notion of a connection makes precise the idea of transporting data along a curve or family of curves in a parallel and consistent manner. There are a variety of kinds of connections in modern geometry, depending on what sort of data one wants to transport...
. On the other hand extrinsic properties relying on an embedding of a surface in Euclidean space have also been extensively studied. This is well illustrated by the non-linear Euler-Lagrange equations in the calculus of variations
Calculus of variations
Calculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
: although Euler developed the one variable equations to understand geodesics, defined independently of an embedding, one of Lagrange's main applications of the two variable equations was to minimal surfaces, a concept that can only be defined in terms of an embedding.
Overview
PolyhedraPolyhedron
In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
in the Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
, such as the boundary of a cube
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
, are among the first surfaces encountered in geometry. It is also possible to define smooth surfaces, in which each point has a neighborhood diffeomorphic
Diffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
to some open set in E2, the Euclidean plane. This elaboration allows calculus
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
to be applied to surfaces to prove many results.
Two smooth surfaces are diffeomorphic if and only if they are homeomorphic. (The analogous result does not hold for higher-dimensional manifolds.) It follows that closed surfaces are classified up to diffeomorphism by their Euler characteristic
Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
and orientability
Orientability
In mathematics, orientability is a property of surfaces in Euclidean space measuring whether or not it is possible to make a consistent choice of surface normal vector at every point. A choice of surface normal allows one to use the right-hand rule to define a "clockwise" direction of loops in the...
.
Smooth surfaces equipped with Riemannian metrics are of foundational importance in differential geometry. A Riemannian metric endows a surface with notions of geodesic
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
, distance
Distance
Distance is a numerical description of how far apart objects are. In physics or everyday discussion, distance may refer to a physical length, or an estimation based on other criteria . In mathematics, a distance function or metric is a generalization of the concept of physical distance...
, angle
Angle
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
, and area. An important class of such surfaces are the developable surface
Developable surface
In mathematics, a developable surface is a surface with zero Gaussian curvature. That is, it is a "surface" that can be flattened onto a plane without distortion . Conversely, it is a surface which can be made by transforming a plane...
s: surfaces that can be flattened to a plane An without stretching; examples include the cylinder
Cylinder (geometry)
A cylinder is one of the most basic curvilinear geometric shapes, the surface formed by the points at a fixed distance from a given line segment, the axis of the cylinder. The solid enclosed by this surface and by two planes perpendicular to the axis is also called a cylinder...
and the cone
Conical surface
In geometry, a conical surface is the unbounded surface formed by the union of all the straight lines that pass through a fixed point — the apex or vertex — and any point of some fixed space curve — the directrix — that does not contain the apex...
.
In addition, there are properties of surfaces which depend on an embedding of the surface into Euclidean space. These surfaces are the subject of extrinsic geometry. They include
- Minimal surfaceMinimal surfaceIn mathematics, a minimal surface is a surface with a mean curvature of zero.These include, but are not limited to, surfaces of minimum area subject to various constraints....
s are surfaces that minimize the surface area for given boundary conditions; examples include soap filmSoap filmSoap films are thin layers of liquid surrounded by air. For example, if two soap bubbles enters in contact, they merged and a thin film is created in between. Thus, foams are composed of a network of films connected by Plateau borders...
s stretched across a wire frame, catenoidCatenoidA catenoid is a three-dimensional surface made by rotating a catenary curve about its directrix. Not counting the plane, it is the first minimal surface to be discovered. It was found and proved to be minimal by Leonhard Euler in 1744. Early work on the subject was published also by Jean Baptiste...
s and helicoidHelicoidThe helicoid, after the plane and the catenoid, is the third minimal surface to be known. It was first discovered by Jean Baptiste Meusnier in 1776. Its name derives from its similarity to the helix: for every point on the helicoid there is a helix contained in the helicoid which passes through...
s. - Ruled surfaceRuled surfaceIn geometry, a surface S is ruled if through every point of S there is a straight line that lies on S. The most familiar examples are the plane and the curved surface of a cylinder or cone...
s are surfaces that have at least one straight line running through every point; examples include the cylinder and the hyperboloid of one sheet.
Any n-dimensional complex manifold
Complex manifold
In differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....
is, at the same time, a real (2n)-dimensional real manifold. Thus any complex one-manifold (also called a Riemann surface
Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
) is a smooth oriented surface with an associated complex structure. Every closed surface admits complex structures. Any complex algebraic curve
Algebraic curve
In algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
or real algebraic surface
Algebraic surface
In mathematics, an algebraic surface is an algebraic variety of dimension two. In the case of geometry over the field of complex numbers, an algebraic surface has complex dimension two and so of dimension four as a smooth manifold.The theory of algebraic surfaces is much more complicated than that...
is also a smooth surface, possibly with singularities.
Complex structures on a closed oriented surface correspond to conformal equivalence classes of Riemannian metrics on the surface. One version of the uniformization theorem
Uniformization theorem
In mathematics, the uniformization theorem says that any simply connected Riemann surface is conformally equivalent to one of the three domains: the open unit disk, the complex plane, or the Riemann sphere. In particular it admits a Riemannian metric of constant curvature...
(due to Poincaré
Henri Poincaré
Jules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...
) states that any Riemannian metric on an oriented, closed surface is conformally equivalent to an essentially unique metric of constant curvature
Constant curvature
In mathematics, constant curvature in differential geometry is a concept most commonly applied to surfaces. For those the scalar curvature is a single number determining the local geometry, and its constancy has the obvious meaning that it is the same at all points...
. This provides a starting point for one of the approaches to Teichmüller theory, which provides a finer classification of Riemann surfaces than the topological one by Euler characteristic alone.
The uniformization theorem
Uniformization theorem
In mathematics, the uniformization theorem says that any simply connected Riemann surface is conformally equivalent to one of the three domains: the open unit disk, the complex plane, or the Riemann sphere. In particular it admits a Riemannian metric of constant curvature...
states that every smooth Riemannian surface
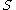 is conformally equivalent
is conformally equivalentConformal equivalence
In mathematics and theoretical physics, two geometries are conformally equivalent if there exists a conformal transformation that maps one geometry to the other one....
to a surface having constant curvature, and the constant may be taken to be 1, 0, or -1. A surface of constant curvature 1 is locally isometric
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
to the sphere, which means that every point on the surface has an open neighborhood that is isometric to an open set on the unit sphere in E3 with its intrinsic Riemannian metric. Likewise, a surface of constant curvature 0 is locally isometric to the Euclidean plane, and a surface of constant curvature -1 is locally isometric to the hyperbolic plane
Hyperbolic geometry
In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
.
Constant curvature surfaces are the two-dimensional realization of what are known as space form
Space form
In mathematics, a space form is a complete Riemannian manifold M of constant sectional curvature K. The three obvious examples are Euclidean n-space, the n-dimensional sphere, and hyperbolic space, although a space form need not be simply connected.-Reduction to generalized crystallography:It is a...
s. These are often studied from the point of view of Felix Klein
Felix Klein
Christian Felix Klein was a German mathematician, known for his work in group theory, function theory, non-Euclidean geometry, and on the connections between geometry and group theory...
's Erlangen programme, by means of smooth transformation groups. Any connected
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
surface with a three-dimensional group of isometries is a surface of constant curvature.
A complex surface is a complex two-manifold and thus a real four-manifold; it is not a surface in the sense of this article. Neither are algebraic curves or surfaces defined over fields
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
other than the complex numbers.
History of surfaces
Isolated properties of surfaces of revolutionSurface of revolution
A surface of revolution is a surface in Euclidean space created by rotating a curve around a straight line in its plane ....
were known already to Archimedes
Archimedes
Archimedes of Syracuse was a Greek mathematician, physicist, engineer, inventor, and astronomer. Although few details of his life are known, he is regarded as one of the leading scientists in classical antiquity. Among his advances in physics are the foundations of hydrostatics, statics and an...
. The development of calculus
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
in the seventeenth century provided a more systematic way of proving them. Curvature of general surfaces was first studied by Euler
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
. In 1760 he proved a formula for the curvature of a plane section of a surface and in 1771 he considered surfaces represented in a parametric form. Monge
Gaspard Monge
Gaspard Monge, Comte de Péluse was a French mathematician, revolutionary, and was inventor of descriptive geometry. During the French Revolution, he was involved in the complete reorganization of the educational system, founding the École Polytechnique...
laid down the foundations of their theory in his classical memoir L'application de l'analyse à la géometrie which appeared in 1795. The defining contribution to the theory of surfaces was made by Gauss
Carl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
in two remarkable papers written in 1825 and 1827. This marked a new departure from tradition because for the first time Gauss considered the intrinsic geometry of a surface, the properties which are determined only by the geodesic distances between points on the surface independently of the particular way in which the surface is located in the ambient Euclidean space. The crowning result, the Theorema Egregium
Theorema Egregium
Gauss's Theorema Egregium is a foundational result in differential geometry proved by Carl Friedrich Gauss that concerns the curvature of surfaces...
of Gauss, established that the Gaussian curvature
Gaussian curvature
In differential geometry, the Gaussian curvature or Gauss curvature of a point on a surface is the product of the principal curvatures, κ1 and κ2, of the given point. It is an intrinsic measure of curvature, i.e., its value depends only on how distances are measured on the surface, not on the way...
is an intrinsic invariant, i.e. invariant under local isometries
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
. This point of view was extended to higher-dimensional spaces by Riemann and led to what is known today as Riemannian geometry
Riemannian geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
. The nineteenth century was the golden age for the theory of surfaces, from both the topological and the differential-geometric point of view, with most leading geometers devoting themselves to their study. Darboux collected many results in his four-volume treatise Théorie des surfaces (1887–1896).
The presentation below largely follows Gauss, but with important later contributions from other geometers. For a time Gauss was Cartographer to George III of Great Britain
Great Britain
Great Britain or Britain is an island situated to the northwest of Continental Europe. It is the ninth largest island in the world, and the largest European island, as well as the largest of the British Isles...
and Hannover; this royal patronage could explain why these papers contain practical calculations of the curvature of the earth based purely on measurements on the surface of the planet.
Curvature of surfaces in E3


The Gaussian curvature at a point on an embedded smooth surface given locally by the equation
- z = F(x,y)
in E3, is defined to be the product of the principal curvature
Principal curvature
In differential geometry, the two principal curvatures at a given point of a surface are the eigenvalues of the shape operator at the point. They measure how the surface bends by different amounts in different directions at that point.-Discussion:...
s at the point;
the mean curvature is defined to be their sum. The principal curvatures are the maximum and minimum curvature
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
s of the plane curve
Plane curve
In mathematics, a plane curve is a curve in a Euclidean plane . The most frequently studied cases are smooth plane curves , and algebraic plane curves....
s obtained by intersecting the surface with planes normal to the tangent plane at the point. If the point is (0, 0, 0) with tangent plane z = 0, then, after a rotation about the z-axis setting the coefficient on xy to zero, F will have the Taylor series expansion
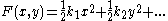
The principal curvatures are k1 and k2 in this case, the Gaussian curvature is given by
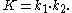 |
and the mean curvature by
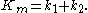 |
Since K and Km are invariant under isometries
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
of E3, in general
| K = (RT − S2)/(1 + P2 + Q2)2 |
and
| Km =(ET + GR – 2FS)/(1 + P2 + Q2)2 |
where the derivatives at the point are given by P = Fx, Q = Fy, R = Fx x, S = Fx y, and T = Fy y.
For every oriented embedded surface the Gauss map
Gauss map
In differential geometry, the Gauss map maps a surface in Euclidean space R3 to the unit sphere S2. Namely, given a surface X lying in R3, the Gauss map is a continuous map N: X → S2 such that N is a unit vector orthogonal to X at p, namely the normal vector to X at p.The Gauss map can be defined...
is the map into the unit sphere sending each point to the (outward pointing) unit normal vector to the oriented tangent plane at the point. In coordinates the map sends (x,y,z) to
- N(x, y, z) = (P2 + Q2 + 1)−1/2·(P, Q, −1).
Direct computation shows that
- the Gaussian curvature is the JacobianJacobian varietyIn mathematics, the Jacobian variety J of a non-singular algebraic curve C of genus g is the moduli space of degree 0 line bundles...
of the Gauss map.
Examples

Surfaces of revolution
A surface of revolutionSurface of revolution
A surface of revolution is a surface in Euclidean space created by rotating a curve around a straight line in its plane ....
can be obtained by rotating a curve in the xz plane about the z-axis, assuming the curve does not intersect the z-axis. Suppose that the curve is given by
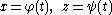
with t lies in (a, b), and is parametrized by arclength, so that
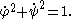
Then the surface of revolution is the point set
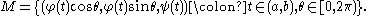
The Gaussian curvature and mean curvature are given by
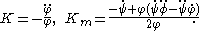

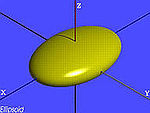
Quadric surfaces
Consider the quadric surface defined by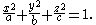
This surface admits a parametrization
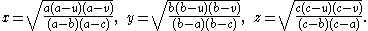
The Gaussian curvature and mean curvature are given by
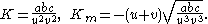

Ruled surfaces
A ruled surfaceRuled surface
In geometry, a surface S is ruled if through every point of S there is a straight line that lies on S. The most familiar examples are the plane and the curved surface of a cylinder or cone...
is one which can be generated by the motion of a straight line in E3. Choosing a directrix on the surface, i.e. a smooth unit speed curve c(t) orthogonal to the straight lines, and then choosing u(t) to be unit vectors along the curve in the direction of the lines, the velocity vector v=ct and u satisfy
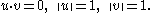
The surface consists of points
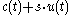
as s and t vary.
Then, if
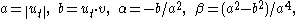
the Gaussian and mean curvature are given by
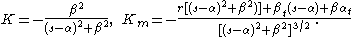
The Gaussian curvature of the ruled surface vanishes if and only if ut and v are proportional, This condition is equivalent to the surface being the envelope of the planes along the curve containing the tangent vector v and the orthogonal vector u, i.e. to the surface being developable
Developable surface
In mathematics, a developable surface is a surface with zero Gaussian curvature. That is, it is a "surface" that can be flattened onto a plane without distortion . Conversely, it is a surface which can be made by transforming a plane...
along the curve. More generally a surface in E3 has vanishing Gaussian curvature near a point if and only if it is developable near that point. (An equivalent condition is given below in terms of the metric.)
Minimal surfaces
In 1760 LagrangeLagrange
La Grange literally means the barn in French. Lagrange may refer to:- People :* Charles Varlet de La Grange , French actor* Georges Lagrange , translator to and writer in Esperanto...
extended Euler's results on the calculus of variations
Calculus of variations
Calculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
involving integrals in one variable to two variables. He had in mind the following problem:
Such a surface is called a minimal surface
Minimal surface
In mathematics, a minimal surface is a surface with a mean curvature of zero.These include, but are not limited to, surfaces of minimum area subject to various constraints....
.
In 1776 Jean Baptiste Meusnier
Jean Baptiste Meusnier
Jean Baptiste Marie Charles Meusnier de la Place was a French mathematician, engineer and Revolutionary general. He is best known for Meusnier's theorem on the curvature of surfaces, which he formulated while he was at the École Royale du Génie . He also discovered the helicoid...
showed that the differential equation derived by Lagrange was equivalent to the vanishing of the mean curvature of the surface:
Minimal surfaces have a simple interpretation in real life: they are the shape a soap film will assume if a wire frame shaped like the curve is dipped into a soap solution and then carefully lifted out. The question as to whether a minimal surface with given boundary exists is called Plateau's problem
Plateau's problem
In mathematics, Plateau's problem is to show the existence of a minimal surface with a given boundary, a problem raised by Joseph-Louis Lagrange in 1760. However, it is named after Joseph Plateau who was interested in soap films. The problem is considered part of the calculus of variations...
after the Belgian physicist Joseph Plateau who carried out experiments on soap films in the mid-nineteenth century. In 1930 Jesse Douglas
Jesse Douglas
Jesse Douglas was an American mathematician. He was born in New York and attended Columbia College of Columbia University from 1920–1924. Douglas was one of two winners of the first Fields Medals, awarded in 1936. He was honored for solving, in 1930, the problem of Plateau, which asks whether a...
and Tibor Radó
Tibor Radó
Tibor Radó was a Hungarian mathematician who moved to the USA after World War I. He was born in Budapest and between 1913 and 1915 attended the Polytechnic Institute. In World War I, he became a First Lieutenant in the Hungarian Army and was captured on the Russian Front...
gave an affirmative answer to Plateau's problem (Douglas was awarded one of the first Fields medal
Fields Medal
The Fields Medal, officially known as International Medal for Outstanding Discoveries in Mathematics, is a prize awarded to two, three, or four mathematicians not over 40 years of age at each International Congress of the International Mathematical Union , a meeting that takes place every four...
s for this work in 1936).
Many explicit examples of minimal surface are known explicitly, such as the catenoid
Catenoid
A catenoid is a three-dimensional surface made by rotating a catenary curve about its directrix. Not counting the plane, it is the first minimal surface to be discovered. It was found and proved to be minimal by Leonhard Euler in 1744. Early work on the subject was published also by Jean Baptiste...
, the helicoid
Helicoid
The helicoid, after the plane and the catenoid, is the third minimal surface to be known. It was first discovered by Jean Baptiste Meusnier in 1776. Its name derives from its similarity to the helix: for every point on the helicoid there is a helix contained in the helicoid which passes through...
, the Scherk surface
Scherk surface
In mathematics, a Scherk surface is an example of a minimal surface. Scherk surfaces arise in the study of certain limiting minimal surface problems and in the study of harmonic diffeomorphisms of hyperbolic space....
and the Enneper surface
Enneper surface
In mathematics, in the fields of differential geometry and algebraic geometry, the Enneper surface is a surface that can be described parametrically by:It was introduced by Alfred Enneper in connection with minimal surface theory....
. There has been extensive research in this area, summarised in . In particular a result of Osserman shows that if a minimal surface is non-planar, then its image under the Gauss map is dense in S2.

Surfaces of constant Gaussian curvature
If a surface has constant Gaussian curvature, it is called a surface of constant curvature.- The unit sphereSphereA sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
in E3 has constant Gaussian curvature +1. - The Euclidean planePlane (mathematics)In mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point , a line and a space...
and the cylinderCylinder (geometry)A cylinder is one of the most basic curvilinear geometric shapes, the surface formed by the points at a fixed distance from a given line segment, the axis of the cylinder. The solid enclosed by this surface and by two planes perpendicular to the axis is also called a cylinder...
both have constant Gaussian curvature 0. - The surfaces of revolution with φtt = φ have constant Gaussian curvature –1. Particular cases are obtained by taking φ(t) = C cosh t, C sinh t and C et. The latter case is the classical pseudospherePseudosphereIn geometry, the term pseudosphere is used to describe various surfaces with constant negative gaussian curvature. Depending on context, it can refer to either a theoretical surface of constant negative curvature, to a tractricoid, or to a hyperboloid....
generated by rotating a tractrixTractrixTractrix is the curve along which a small object moves, under the influence of friction, when pulled on a horizontal plane by a piece of thread and a puller that moves at a right angle to the initial line between the object and the puller at an infinitesimal speed. It is therefore a curve of...
around a central axis. In 1868 BeltramiBeltramiBeltrami may refer to:People*Eugenio Beltrami, Italian mathematician*Giacomo Beltrami, Italian count for whom the Minnesota county is named, and who claimed to have discovered the Mississippi River headwaters*Joseph Beltrami, Scottish lawyer...
showed that the geometry of the pseudosphere was directly related to that of the hyperbolic planeHyperbolic geometryIn mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
, discovered independently by Lobachevsky (1830) and Bolyai (1832) . Already in 1840, F. Minding, a student of Gauss, had obtained trigonometric formulas for the pseudosphere identical to those for the hyperbolic plane. This surface of constant curvature is now better understood in terms of the Poincaré metricPoincaré metricIn mathematics, the Poincaré metric, named after Henri Poincaré, is the metric tensor describing a two-dimensional surface of constant negative curvature. It is the natural metric commonly used in a variety of calculations in hyperbolic geometry or Riemann surfaces.There are three equivalent...
on the upper half plane or the unit disc, and has been described by other models such as the Klein modelKlein modelIn geometry, the Beltrami–Klein model, also called the projective model, Klein disk model, and the Cayley–Klein model, is a model of n-dimensional hyperbolic geometry in which points are represented by the points in the interior of the n-dimensional unit ball and lines are represented by the...
or the hyperboloid modelHyperboloid modelIn geometry, the hyperboloid model, also known as the Minkowski model or the Lorentz model , is a model of n-dimensional hyperbolic geometry in which points are represented by the points on the forward sheet S+ of a two-sheeted hyperboloid in -dimensional Minkowski space and m-planes are...
, obtained by considering the two-sheeted hyperboloid q(x, y, z) = −1 in three-dimensional Minkowski spaceMinkowski spaceIn physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
, where q(x, y, z) = x2 + y2 – z2.
Each of these surfaces of constant curvature has a transitive Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
of symmetries. This group theoretic fact has far-reaching consequences, all the more remarkable because of the central role these special surfaces play in the geometry of surfaces, due to Poincaré
Poincaré
Several members of the French Poincaré family have been successful in public and scientific life:* Henri Poincaré , physicist, mathematician and philosopher of science* Lucien Poincaré , physicist, brother of Raymond and cousin of Henri...
's uniformization theorem
Uniformization theorem
In mathematics, the uniformization theorem says that any simply connected Riemann surface is conformally equivalent to one of the three domains: the open unit disk, the complex plane, or the Riemann sphere. In particular it admits a Riemannian metric of constant curvature...
(see below).
Other examples of surfaces with Gaussian curvature 0 include cones
Cone (geometry)
A cone is an n-dimensional geometric shape that tapers smoothly from a base to a point called the apex or vertex. Formally, it is the solid figure formed by the locus of all straight line segments that join the apex to the base...
, tangent developable
Tangent developable
The tangent developable of a space curve \gamma is a ruled surface of the form \gamma+s \gamma^\prime. Intuitively it is the union of the tangent lines to the space curve....
s, and more generally any developable surface.
Local metric structure

Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
, a topological space where the smooth structure
Smooth structure
In mathematics, a smooth structure on a manifold allows for an unambiguous notion of smooth function. In particular, a smooth structure allows one to perform mathematical analysis on the manifold....
is given by local charts on the manifold, exactly as the planet Earth
Earth
Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
is mapped by atlas
Atlas
An atlas is a collection of maps; it is typically a map of Earth or a region of Earth, but there are atlases of the other planets in the Solar System. Atlases have traditionally been bound into book form, but today many atlases are in multimedia formats...
es today. Changes of coordinates between different charts of the same region are required to be smooth. Just as contour lines on real-life maps encode changes in elevation, taking into account local distortions of the Earth's surface to calculate true distances, so the Riemannian metric describes distances and areas "in the small" in each local chart. In each local chart a Riemannian metric is given by smoothly assigning a 2 x 2 positive definite matrix to each point; when a different chart is taken, the matrix is transformed according to the Jacobian matrix of the coordinate change. The manifold then has the structure of a 2-dimensional Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
.
Line and area elements
Taking a local chart, for example by projecting onto the x-y plane (z = 0), the line element ds and the area element dA can be written in terms of local coordinates as- ds2 = E dx2 + 2F dx dy + G dy2
and
- dA = (EG − F2)1/2 dx dy.
The expression E dx2 + 2F dx dy + G dy2 is called the first fundamental form.
The matrix
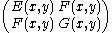
is required to be positive-definite
Positive-definite matrix
In linear algebra, a positive-definite matrix is a matrix that in many ways is analogous to a positive real number. The notion is closely related to a positive-definite symmetric bilinear form ....
and to depend smoothly on x and y.
In a similar way line and area elements can be associated to any abstract Riemannian 2-manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
in a local chart.
Second fundamental form
The extrinsic geometry of surfaces studies the properties of surfaces embedded into a Euclidean space, typically E3. In intrinsic geometry, two surfaces are "the same" if it is possible to unfold one surface onto the other without stretching it, i.e. a map of one surface onto the other preserving distance. Thus a cylinder is locally "the same" as the plane. In extrinsic geometry, two surfaces are "the same" if they are congruentCongruence (geometry)
In geometry, two figures are congruent if they have the same shape and size. This means that either object can be repositioned so as to coincide precisely with the other object...
in the ambient Euclidean space, i.e. there is an isometry
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
of E3 carrying one surface onto the other. With this more rigid definition of similitude, the cylinder and the plane are obviously no longer the same.
Although the primary invariant in the study of the intrinsic geometry of surfaces is the metric (the first fundamental form) and the Gaussian curvature, certain properties of surfaces also depend on an embedding into E3 (or a higher dimensional Euclidean space). The most important example is the second fundamental form, defined classically as follows.
Take a point (x, y) on the surface in a local chart. The square of the Euclidean distance from a nearby point (x + dx, y + dy) to the tangent plane at (x, y), i.e. the square of the length of the perpendicular dropped from the nearby point to the tangent plane, has the form
- e dx2 + 2f dx dy + g dy2
plus third and higher order corrections. The above expression, a symmetric bilinear form at each point, is the second fundamental form.
It is described by a 2 × 2 symmetric matrix
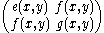
which depends smoothly on x and y. The Gaussian curvature can be calculated as the ratio of the determinants of the second and first fundamental forms:
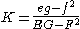 |
Remarkably Gauss proved that it is an intrinsic invariant (see his Theorema Egregium below).
One of the other extrinisic numerical invariants of a surface is the mean curvature
Mean curvature
In mathematics, the mean curvature H of a surface S is an extrinsic measure of curvature that comes from differential geometry and that locally describes the curvature of an embedded surface in some ambient space such as Euclidean space....
Km, defined as the sum of the principal curvatures. It is given by the formula
 |
The coefficients of the first and second fundamental forms satisfy certain compatibility conditions known as the Gauss-Codazzi equations;
they involve the Christoffel symbols
Christoffel symbols
In mathematics and physics, the Christoffel symbols, named for Elwin Bruno Christoffel , are numerical arrays of real numbers that describe, in coordinates, the effects of parallel transport in curved surfaces and, more generally, manifolds. As such, they are coordinate-space expressions for the...
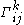 associated with the first fundamental form:
associated with the first fundamental form: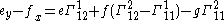
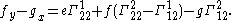
These equations can also be succinctly expressed and derived in the language of connection form
Connection form
In mathematics, and specifically differential geometry, a connection form is a manner of organizing the data of a connection using the language of moving frames and differential forms....
s due to Élie Cartan
Élie Cartan
Élie Joseph Cartan was an influential French mathematician, who did fundamental work in the theory of Lie groups and their geometric applications...
. Pierre Bonnet
Pierre Ossian Bonnet
Pierre Ossian Bonnet was a French mathematician. He made some important contributions to the differential geometry of surfaces, including the Gauss-Bonnet theorem.-Early years:...
proved that two quadratic forms satisfying the Gauss-Codazzi equations always uniquely determine an embedded surface locally. For this reason the Gauss-Codazzi equations are often called the fundamental equations for embedded surfaces, precisely identifying where the intrinsic and extrinsic curvatures come from. They admit generalizations to surfaces embedded in more general Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
s.
Shape operator
The differentialDifferential of a function
In calculus, the differential represents the principal part of the change in a function y = ƒ with respect to changes in the independent variable. The differential dy is defined bydy = f'\,dx,...
df of the Gauss map f can be used to define a type of extrinsic curvature, known as the shape operator or Weingarten map. This operator first appeared implicitly in the work of Wilhelm Blaschke
Wilhelm Blaschke
Wilhelm Johann Eugen Blaschke was an Austro-Hungarian differential and integral geometer.His students included Shiing-Shen Chern, Luis Santaló, and Emanuel Sperner....
and later explicitly in a treatise by Burali-Forti and Burgati.
Since at each point x of the surface, the tangent space is an inner product space, the shape operator Sx can be defined as a linear operator on this space by the formula
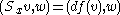
for tangent vectors v, w (the inner product makes sense because df(v) and w both lie in E3). The right hand side is symmetric in v and w, so the shape operator is self-adjoint on the tangent space. The eigenvalues of Sx are just the principal curvatures k1 and k2 at x. In particular the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of the shape operator at a point is the Gaussian curvature, but it also contains other information, since the mean curvature
Mean curvature
In mathematics, the mean curvature H of a surface S is an extrinsic measure of curvature that comes from differential geometry and that locally describes the curvature of an embedded surface in some ambient space such as Euclidean space....
is half the trace
Trace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
of the shape operator. The mean curvature is an extrinsic invariant. In intrinsic geometry, a cylinder is developable, meaning that every piece of it is intrinsically indistinguishable from a piece of a plane since its Gauss curvature vanishes identically. Its mean curvature is not zero, though; hence extrinsically it is different from a plane.
In general, the eigenvectors and eigenvalues
Eigenvalue, eigenvector and eigenspace
The eigenvectors of a square matrix are the non-zero vectors that, after being multiplied by the matrix, remain parallel to the original vector. For each eigenvector, the corresponding eigenvalue is the factor by which the eigenvector is scaled when multiplied by the matrix...
of the shape operator at each point determine the directions in which the surface bends at each point. The eigenvalues correspond to the principal curvatures of the surface and the eigenvectors are the corresponding principal directions. The principal directions specify the directions that a curve embedded in the surface must travel to have maximum and minimum curvature, these being given by the principal curvatures.
The shape operator is given in terms of the components of the first and second fundamental forms by the Weingarten equations
Weingarten equations
Weingarten equations give expansion of the derivative of the unit normal vector to a surface in terms of the first derivatives of the position vector of this surface...
:
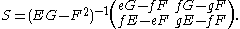
Geodesic curves on a surface
Curves on a surface which minimize length between the endpoints are called geodesicGeodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
s; they are the shape that an elastic band stretched between the two points would take. Mathematically they are described using partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s from the calculus of variations
Calculus of variations
Calculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
. The differential geometry of surfaces revolves around the study of geodesics. It is still an open question whether every Riemannian metric on a 2-dimensional local chart arises from an embedding in 3-dimensional Euclidean space: the theory of geodesics has been used to show this is true in the important case when the components of the metric are analytic
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
.
Geodesics

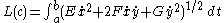
and energy by
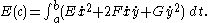
The length is independent of the parametrisation of a path. By the Euler-Lagrange equations, if c(t) is a path minimising length, parametrised by arclength, it must satisfy the Euler equations
Euler equations
In fluid dynamics, the Euler equations are a set of equations governing inviscid flow. They are named after Leonhard Euler. The equations represent conservation of mass , momentum, and energy, corresponding to the Navier–Stokes equations with zero viscosity and heat conduction terms. Historically,...
 + Γ¹11
+ Γ¹11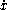 ² + 2Γ¹12
² + 2Γ¹12 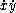 + Γ¹22
+ Γ¹22 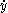 ² =0 and
² =0 and 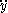 + Γ²11
+ Γ²11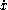 ² + 2Γ²12
² + 2Γ²12 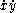 + Γ²22
+ Γ²22 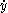 ² =0
² =0where the Christoffel symbols
Christoffel symbols
In mathematics and physics, the Christoffel symbols, named for Elwin Bruno Christoffel , are numerical arrays of real numbers that describe, in coordinates, the effects of parallel transport in curved surfaces and, more generally, manifolds. As such, they are coordinate-space expressions for the...
Γkij are given by
- Γkij =
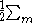 g km (
g km (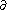 j gim +
j gim + i gjm –
i gjm – 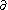 m gij)
m gij)
where g11 = E, g12=F, g22 =G and (gij) is the inverse matrix to (gij). A path satisfying the Euler equations is called a geodesic
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
.
By the Cauchy-Schwarz inequality a path minimising energy is just a geodesic parametrised by arc length; and, for any geodesic, the parameter t is proportional to arclength.
Geodesic curvature
The geodesic curvature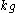 at a point of a curve c(t), parametrised by arc length, on an oriented surface is defined to be
at a point of a curve c(t), parametrised by arc length, on an oriented surface is defined to be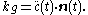
where n(t) is the "principal" unit normal to the curve in the surface, constructed by rotating the unit tangent vector
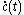 through an angle of + 90°.
through an angle of + 90°.- The geodesic curvature at a point is an intrinsic invariant depending only on the metric near the point.
- A unit speed curve on a surface is a geodesic if and only if its geodesic curvature vanishes at all points on the curve.
- A unit speed curve c(t) in an embedded surface is a geodesic if and only if its acceleration vector
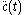 is normal to the surface.
is normal to the surface.
The geodesic curvature measures in a precise way how far a curve on the surface is from being a geodesic.
Isometric embedding problem
A result of and shows that every metric structure on a surface arises from a local embedding in E4.Apart from some special cases, whether this is possible in E3 remains an open question, the so-called "Weyl problem". In 1926 Maurice Janet proved that it is always possible locally if E, F and G are analytic
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
; soon afterwards Élie Cartan
Élie Cartan
Élie Joseph Cartan was an influential French mathematician, who did fundamental work in the theory of Lie groups and their geometric applications...
generalised this to local embeddings of Riemannian n-manifolds
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
in Em where m = ½(n² +n). To prove Janet's theorem near (0,0), the Cauchy-Kowalevski theorem is used twice to produce analytic geodesics orthogonal to the y-axis and then the x-axis to make an analytic change of coordinate so that E=1 and F=0. An isometric embedding u must satisfy
- ux • ux =1, ux • uy = 0, uy • uy = G.
Differentiating gives the three additional equations
- uxx • uy = 0, uxx • ux = 0, uxx • uyy = uxy • ux y - ½ Gxx
with u(0,y) and ux(0,y) prescribed. These equations can be solved near (0,0) using the Cauchy-Kowalevski theorem and yield a solution
of the original embedding equations.
Orthogonal coordinates
When F=0 in the metric, lines parallel to the x- and y-axes are orthogonal and provide orthogonal coordinatesOrthogonal coordinates
In mathematics, orthogonal coordinates are defined as a set of d coordinates q = in which the coordinate surfaces all meet at right angles . A coordinate surface for a particular coordinate qk is the curve, surface, or hypersurface on which qk is a constant...
. If H=(EG)½, then the Gaussian curvature is given by
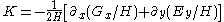 |
If in addition E=1, so that H=G½, then the angle
 at the intersection between geodesic (x(t),y(t)) and the line y = constant is given by the equation
at the intersection between geodesic (x(t),y(t)) and the line y = constant is given by the equation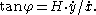
The derivative of
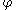 is given by a classical derivative formula of Gauss:
is given by a classical derivative formula of Gauss: |
Geodesic polar coordinates
Once a metric is given on a surface and a base point is fixed, there is a unique geodesic connecting the base point to each sufficiently nearby point. The direction of the geodesic at the base point and the distance uniquely determine the other endpoint. These two bits of data, a direction and a magnitude, thus determine a tangent vector at the base point. The map from tangent vectors to endpoints smoothly sweeps out a neighbourhood of the base point and defines what is called the "exponential map", defining a local coordinate chart at that base point. The neighbourhood swept out has similar properties to balls in Euclidean space, namely any two points in it are joined by a unique geodesic. This property is called "geodesic convexity" and the coordinates are called "normal coordinates". The explicit calculation of normal coordinates can be accomplished by considering the differential equation satisfied by geodesics. The convexity properties are consequences of Gauss's lemmaGauss's lemma (Riemannian geometry)
In Riemannian geometry, Gauss's lemma asserts that any sufficiently small sphere centered at a point in a Riemannian manifold is perpendicular to every geodesic through the point. More formally, let M be a Riemannian manifold, equipped with its Levi-Civita connection, and p a point of M...
and its generalisations. Roughly speaking this lemma states that geodesics starting at the base point must cut the spheres of fixed radius centred on the base point at right angles. Geodesic polar coordinates are obtained by combining the exponential map with polar coordinates on tangent vectors at the base point.
The Gaussian curvature of the surface is then given by the second order deviation of the metric at the point from the Euclidean metric. In particular the Gaussian curvature is an invariant of the metric, Gauss's celebrated Theorema Egregium
Theorema Egregium
Gauss's Theorema Egregium is a foundational result in differential geometry proved by Carl Friedrich Gauss that concerns the curvature of surfaces...
. A convenient way to understand the curvature comes from an ordinary differential equation, first considered by Gauss and later generalized by Jacobi, arising from the change of normal coordinates about two different points. The Gauss–Jacobi equation provides another way of computing the Gaussian curvature. Geometrically it explains what happens to geodesics from a fixed base point as the endpoint varies along a small curve segment through data recorded in the Jacobi field
Jacobi field
In Riemannian geometry, a Jacobi field is a vector field along a geodesic \gamma in a Riemannian manifold describing the difference between the geodesic and an "infinitesimally close" geodesic. In other words, the Jacobi fields along a geodesic form the tangent space to the geodesic in the space...
, a vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
along the geodesic. One and a quarter centuries after Gauss and Jacobi, Marston Morse
Marston Morse
Harold Calvin Marston Morse was an American mathematician best known for his work on the calculus of variations in the large, a subject where he introduced the technique of differential topology now known as Morse theory...
gave a more conceptual interpretation of the Jacobi field in terms of second derivatives of the energy function on the infinite-dimensional Hilbert manifold
Hilbert manifold
In mathematics, a Hilbert manifold is a manifold modeled on Hilbert spaces. Thus it is a separable Hausdorff space in which each point has a neighbourhood homeomorphic to an infinite dimensional Hilbert space. The concept of a Hilbert manifold provides a possibility of extending the theory of...
of paths.
Exponential map
The theory of ordinary differential equationOrdinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
s shows that if f(t, v) is smooth then the differential equation
dv/dt = f(t,v) with initial condition v(0) = v0 has a unique solution for |t| sufficiently small and the solution depends smoothly
on t and v0. This implies that for sufficiently small tangent vector
Tangent vector
A tangent vector is a vector that is tangent to a curve or surface at a given point.Tangent vectors are described in the differential geometry of curves in the context of curves in Rn. More generally, tangent vectors are elements of a tangent space of a differentiable manifold....
s v at a given point p = (x0,y0), there is a geodesic cv(t) defined on (−2,2) with cv(0) = (x0,y0) and
 v(0) = v. Moreover if |s| ≤ 1, then csv = cv(st). The exponential map is defined by
v(0) = v. Moreover if |s| ≤ 1, then csv = cv(st). The exponential map is defined by
- expp(v) = cv (1)
and gives a diffeomorphism between a disc ||v|| < δ and a neighbourhood of p; more generally the map sending (p,v) to expp(v) gives a local diffeomorphism onto a neighbourhood of (p,p). The exponential map gives geodesic normal coordinates near p.
Computation of normal coordinates
There is a standard technique (see for example ) for computing the change of variables to normal coordinates u, v at a point as a formal Taylor series expansion. If the coordinates x, y at (0,0) are locally orthogonal, write- x(u,v) = α u + L(u,v) + λ(u,v) + ···
- y(u,v) = β v + M(u,v) + μ(u,v) + ···
where L, M are quadratic and λ, μ cubic homogeneous polynomials in u and v. If u and v are fixed, x(t) = x(tu,tv) and y(t) = y(tu, tv) can be considered as formal power series solutions of the Euler equations: this uniquely determines α, β, L, M, λ and μ.
Gauss's lemma
In these coordinates the matrix g(x) satisfies g(0) = I and the lines t tv are geodesics through 0. Euler's equations imply the matrix equation- g(v)v = v,
a key result, usually called the Gauss lemma
Gauss's lemma (Riemannian geometry)
In Riemannian geometry, Gauss's lemma asserts that any sufficiently small sphere centered at a point in a Riemannian manifold is perpendicular to every geodesic through the point. More formally, let M be a Riemannian manifold, equipped with its Levi-Civita connection, and p a point of M...
. Geometrically it states that
| the geodesics through 0 cut the circles centred at 0 orthogonally. |
Taking polar coordinates (r,θ), it follows that the metric has the form
- ds2 = dr2 + G(r,θ) dθ2.
In geodesic coordinates, it is easy to check that the geodesics through zero minimize length. The topology on the Riemannian manifold is then given by a distance function d(p,q), namely the infimum
Infimum
In mathematics, the infimum of a subset S of some partially ordered set T is the greatest element of T that is less than or equal to all elements of S. Consequently the term greatest lower bound is also commonly used...
of the lengths of piecewise smooth paths between p and q. This distance is realised locally by geodesics,
so that in normal coordinates d(0,v) = ||v||. If the radius δ is taken small enough, a slight sharpening of the Gauss lemma shows that the image U of the
disc ||v|| < δ under the exponential map is geodesically convex, i.e. any two points in U are joined by a unique geodesic lying entirely inside U.
Theorema Egregium
Taking x and y coordinates of a surface in E3 corresponding to F(x,y) =k1 x2 + k2 y2 + ···, the power series expansion of the metric is given in normal coordinates (u, v) as
- ds2 = du2 + dv2 + K(u dv – v du)2 + ···
This extraordinary result — Gauss' Theorema Egregium
Theorema Egregium
Gauss's Theorema Egregium is a foundational result in differential geometry proved by Carl Friedrich Gauss that concerns the curvature of surfaces...
— shows that the Gaussian curvature of a surface can be computed solely in terms of the metric
and is thus an intrinsic invariant of the surface, independent of any embedding in E³ and unchanged under coordinate transformations. In particular isometries of surfaces preserve Gaussian curvature.
Gauss–Jacobi equation
Taking a coordinate change from normal coordinates at p to normal coordinates at a nearby point q, yields the Sturm–Liouville equation satisfied by H(r,θ) = G(r,θ)½, discovered by Gauss and later generalisedJacobi field
In Riemannian geometry, a Jacobi field is a vector field along a geodesic \gamma in a Riemannian manifold describing the difference between the geodesic and an "infinitesimally close" geodesic. In other words, the Jacobi fields along a geodesic form the tangent space to the geodesic in the space...
by Jacobi
Carl Gustav Jakob Jacobi
Carl Gustav Jacob Jacobi was a German mathematician, widely considered to be the most inspiring teacher of his time and is considered one of the greatest mathematicians of his generation.-Biography:...
,
| Hrr = – K H |
The Jacobian of this coordinate change at q is equal to Hr. This gives another way of establishing the intrinsic nature of Gaussian curvature. Because H(r,θ) can be interpreted as the length of the line element in the θ direction, the Gauss–Jacobi equation shows that the Gaussian curvature measures the spreading of geodesics on a geometric surface as they move away from a point.
Laplace–Beltrami operator
On a surface with local metric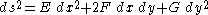
and Laplace–Beltrami operator
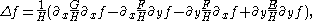
where H2 = EG – F 2, the Gaussian curvature at a point is given by the formula
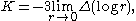
where r is the denotes the geodesic distance from the point.
Since Δ is manifestly an intrinsic invariant, this gives yet another proof that the Gaussian curvature is an intrinsic invariant.
In isothermal coordinates
Isothermal coordinates
In mathematics, specifically in differential geometry, isothermal coordinates on a Riemannian manifoldare local coordinates where the metric isconformal to the Euclidean metric...
, first considered by Gauss, the metric is required to be of the special form
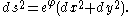
In this case the Laplace–Beltrami operator is given by
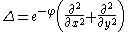
and φ satisfies Liouville's equation
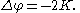
Isothermal coordinates are known to exist in a neighbourhood of any point on the surface, although all proofs to date rely on non-trivial results on partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s. There is an elementary proof for minimal surfaces.
Gauss–Bonnet theorem

Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
or a hyperboloid, the area of a geodesic triangle, i.e. a triangle all the sides of which are geodesics, is proportional to the difference of the sum of the interior angles and π. The constant of proportionality is just the Gaussian curvature, a constant for these surfaces. For the torus, the difference is zero, reflecting the fact that its Gaussian curvature is zero. These are standard results in spherical, hyperbolic and high school trigonometry (see below). Gauss generalised these results to an arbitrary surface by showing that the integral of the Gaussian curvature over the interior of a geodesic triangle is also equal to this angle difference or excess. His formula showed that the Gaussian curvature could be calculated near a point as the limit of area over angle excess for geodesic triangles shrinking to the point. Since any closed surface can be decomposed up into geodesic triangles, the formula could also be used to compute the integral of the curvature over the whole surface. As a special case of what is now called the Gauss-Bonnet theorem, Gauss proved that this integral was remarkably always 2π times an integer, a topological invariant of the surface called the Euler characteristic
Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
. This invariant is easy to compute combinatorially in terms of the number of vertices, edges, and faces of the triangles in the decomposition, also called a triangulation
Triangulation (topology)
In mathematics, topology generalizes the notion of triangulation in a natural way as follows:A triangulation of a topological space X is a simplicial complex K, homeomorphic to X, together with a homeomorphism h:K\to X....
. This interaction between analysis and topology was the forerunner of many later results in geometry, culminating in the Atiyah-Singer index theorem. In particular properties of the curvature impose restrictions on the topology of the surface.
Geodesic triangles
Gauss proved that, if Δ is a geodesic triangle on a surface with angles α, β and γ at vertices A, B and C, then Δ K dA = α + β + γ − π. Δ K dA = α + β + γ − π. |
In fact taking geodesic polar coordinates with origin A and AB, AC the radii at polar angles 0 and α
 Δ K dA =
Δ K dA =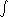 Δ KH dr dθ = –
Δ KH dr dθ = – 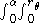 Hrr dr dθ =
Hrr dr dθ = 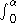 1 − Hr(rθ,θ) dθ =
1 − Hr(rθ,θ) dθ = 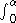 dθ +
dθ + 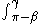 dφ = α + β + γ − π,
dφ = α + β + γ − π,where the second equality follows from the Gauss–Jacobi equation and the fourth from Gauss' derivative formula in the orthogonal coordinates (r,θ).
Gauss' formula shows that the curvature at a point can be calculated as the limit of angle excess α + β + γ − π over area for successively smaller geodesic triangles near the point. Qualitatively a surface is positively or negatively curved according to the sign of the angle excess for arbitrarily small geodesic triangles.
Gauss-Bonnet theorem

Since every compact oriented 2-manifold M can be triangulated
Triangulation (topology)
In mathematics, topology generalizes the notion of triangulation in a natural way as follows:A triangulation of a topological space X is a simplicial complex K, homeomorphic to X, together with a homeomorphism h:K\to X....
by small geodesic triangles, it follows that
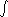 M K dA = 2π·χ(M) M K dA = 2π·χ(M) |
where χ(M) denotes the Euler characteristic
Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
of the surface.
In fact if there are F faces, E edges and V vertices, then 3F = 2E and the left hand side equals 2π·V – π·F = 2π·(V – E + F) = 2π·χ(M).
This is the celebrated Gauss-Bonnet theorem: it shows that the integral of the Gaussian curvature is a topological invariant of the manifold, namely the Euler characteristic. This theorem can be interpreted in many ways; perhaps one of the most far-reaching has been as the index theorem for an elliptic differential operator on M, one of the simplest cases of the Atiyah-Singer index theorem. Another related result, which can be proved using the Gauss-Bonnet theorem, is the Poincaré-Hopf index theorem for vector fields on M which vanish at only a finite number of points: the sum of the indices
Index (mathematics)
The word index is used in variety of senses in mathematics.- General :* In perhaps the most frequent sense, an index is a number or other symbol that indicates the location of a variable in a list or array of numbers or other mathematical objects. This type of index is usually written as a...
at these points equals the Euler characteristic. (On a small circle round each isolated zero, the vector field defines a map into the unit circle; the index is just the winding number
Winding number
In mathematics, the winding number of a closed curve in the plane around a given point is an integer representing the total number of times that curve travels counterclockwise around the point...
of this map.)
Curvature and embeddings
If the Gaussian curvature of a surface M is everywhere positive, then the Euler characteristic is positive so M is homeomorphic (and therefore diffeomorphic) to S2. If in addition the surface is isometrically embedded in E3, the Gauss map provides an explicit diffeomorphism. As HadamardJacques Hadamard
Jacques Salomon Hadamard FRS was a French mathematician who made major contributions in number theory, complex function theory, differential geometry and partial differential equations.-Biography:...
observed, in this case the surface is convex
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
; this criterion for convexity can be viewed as a 2-dimensional generalisation of the well-known second derivative criterion for convexity of plane curves. Hilbert
David Hilbert
David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
proved that every isometrically embedded closed surface must have a point of positive curvature. Thus a closed Riemannian 2-manifold of non-positive curvature can never be embedded isometrically in E3; however, as Adriano Garsia
Adriano Garsia
Adriano Mario Garsia is an Italian American mathematician, a leading expert in combinatorics, representation theory, and algebraic geometry, a student of Charles Loewner. He has made many deep contributions to representation theory, symmetric functions and algebraic combinatorics, which exerted a...
showed using the Beltrami equation for quasiconformal mapping
Quasiconformal mapping
In mathematical complex analysis, a quasiconformal mapping, introduced by and named by , is a homeomorphism between plane domains which to first order takes small circles to small ellipses of bounded eccentricity....
s, this is always possible for some conformally equivalent
Conformal equivalence
In mathematics and theoretical physics, two geometries are conformally equivalent if there exists a conformal transformation that maps one geometry to the other one....
metric.
Surfaces of constant curvature
The simply connected surfaces of constant curvature 0, +1 and –1 are the Euclidean plane, the unit sphere in E3, and the hyperbolic planeHyperbolic geometry
In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
. Each of these has a transitive three-dimensional Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
of orientation preserving isometries
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
G, which can be used to study their geometry. Each of the two non-compact surfaces can be identified with the quotient G / K where K is a maximal compact subgroup
Maximal compact subgroup
In mathematics, a maximal compact subgroup K of a topological group G is a subgroup K that is a compact space, in the subspace topology, and maximal amongst such subgroups....
of G. Here K is isomorphic to SO(2). Any other closed Riemannian 2-manifold M of constant Gaussian curvature, after scaling the metric by a constant factor if necessary, will have one of these three surfaces as its universal covering space. In the orientable case, the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
Γ of M can be identified with a torsion-free
Torsion-free
In mathematics, the term torsion-free may refer to several unrelated notions:* In abstract algebra, a group is torsion-free if the only element of finite order is the identity....
uniform subgroup
Lattice (discrete subgroup)
In Lie theory and related areas of mathematics, a lattice in a locally compact topological group is a discrete subgroup with the property that the quotient space has finite invariant measure...
of G and M can then be identified with the double coset space
Double coset
In mathematics, an double coset in G, where G is a group and H and K are subgroups of G, is an equivalence class for the equivalence relation defined on G by...
Γ \ G / K. In the case of the sphere and the Euclidean plane, the only possible examples are the sphere itself and tori obtained as quotients of R2 by discrete rank 2 subgroups. For closed surfaces of genus
Genus
In biology, a genus is a low-level taxonomic rank used in the biological classification of living and fossil organisms, which is an example of definition by genus and differentia...
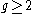 , the moduli space
, the moduli spaceModuli space
In algebraic geometry, a moduli space is a geometric space whose points represent algebro-geometric objects of some fixed kind, or isomorphism classes of such objects...
of Riemann surfaces obtained as Γ varies over all such subgroups, has real dimension 6g - 6 . By Poincaré's uniformization theorem
Uniformization theorem
In mathematics, the uniformization theorem says that any simply connected Riemann surface is conformally equivalent to one of the three domains: the open unit disk, the complex plane, or the Riemann sphere. In particular it admits a Riemannian metric of constant curvature...
, any orientable closed 2-manifold is conformally equivalent
Conformal equivalence
In mathematics and theoretical physics, two geometries are conformally equivalent if there exists a conformal transformation that maps one geometry to the other one....
to a surface of constant curvature 0, +1 or –1. In other words, by multiplying the metric by a positive scaling factor, the Gaussian curvature can be made to take exactly one of these values (the sign of the Euler characteristic
Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
of M).
Euclidean geometry

Euclidean group
In mathematics, the Euclidean group E, sometimes called ISO or similar, is the symmetry group of n-dimensional Euclidean space...
, the semidirect product
Semidirect product
In mathematics, specifically in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup. A semidirect product is a generalization of a direct product...
of
the two dimensional group of translations by the group of rotations. Geodesics are straight lines and the geometry is encoded in the elementary formulas of trigonometry
Trigonometry
Trigonometry is a branch of mathematics that studies triangles and the relationships between their sides and the angles between these sides. Trigonometry defines the trigonometric functions, which describe those relationships and have applicability to cyclical phenomena, such as waves...
, such as the cosine rule for a triangle with sides a, b, c and angles α, β, γ:
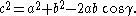
Flat tori can be obtained by taking the quotient of R2 by a lattice, i.e. a free Abelian subgroup of rank 2. These closed surfaces have no isometric embeddings in E3. They do nevertheless admit isometric embeddings in E4; in the easiest case this follows from the fact that the torus is a product of two circles and each circle can be isometrically embedded in E2.
Spherical geometry

Rotation group
In mechanics and geometry, the rotation group is the group of all rotations about the origin of three-dimensional Euclidean space R3 under the operation of composition. By definition, a rotation about the origin is a linear transformation that preserves length of vectors and preserves orientation ...
SO(3) as the subgroup of isometries preserving orientation. It is the direct product of SO(3) with the antipodal map, sending x to –x. The group SO(3) acts transitively on S2. The stabilizer subgroup of the unit vector (0,0,1) can be identified with SO(2), so that S2 = SO(3)/SO(2).
The geodesics between two points on the sphere are the great circle
Great circle
A great circle, also known as a Riemannian circle, of a sphere is the intersection of the sphere and a plane which passes through the center point of the sphere, as opposed to a general circle of a sphere where the plane is not required to pass through the center...
arcs with these given endpoints. If the points are not antipodal, there is a unique shortest geodesic between the points. The geodesics can also be described group theoretically: each geodesic through the North pole (0,0,1) is the orbit of the subgroup of rotations about an axis through antipodal points on the equator.
A spherical triangle is a geodesic triangle on the sphere. It is defined by points A, B, C on the sphere with sides BC, CA, AB formed from great circle arcs of length less than π. If the lengths of the sides are a, b, c and the angles between the sides α, β, γ,
then the spherical cosine law states that
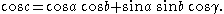
The area of the triangle is given by
- Area = α + β + γ - π.
Using stereographic projection
Stereographic projection
The stereographic projection, in geometry, is a particular mapping that projects a sphere onto a plane. The projection is defined on the entire sphere, except at one point — the projection point. Where it is defined, the mapping is smooth and bijective. It is conformal, meaning that it...
from the North pole, the sphere can be identified with the extended complex plane C
 {∞}. The explicit map is given by
{∞}. The explicit map is given by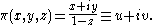
Under this correspondence every rotation of S2 corresponds to a Möbius transformation in SU(2), unique up to sign. With respect to the coordinates (u, v) in the complex plane, the spherical metric becomes
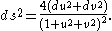
The unit sphere is the unique closed orientable surface with constant curvature +1. The quotient SO(3)/O(2) can be identified with the real projective plane
Real projective plane
In mathematics, the real projective plane is an example of a compact non-orientable two-dimensional manifold, that is, a one-sided surface. It cannot be embedded in our usual three-dimensional space without intersecting itself...
. It is non-orientable and can be described as the quotient of S2 by the antipodal map (multiplication by –1). The sphere is simply connected, while the real projective plane has fundamental group Z2. The finite subgroups of SO(3)
Point groups in three dimensions
In geometry, a point group in three dimensions is an isometry group in three dimensions that leaves the origin fixed, or correspondingly, an isometry group of a sphere. It is a subgroup of the orthogonal group O, the group of all isometries that leave the origin fixed, or correspondingly, the group...
, corresponding to the finite subgroups of O(2) and the symmetry groups of the platonic solids, do not act freely on S2, so the corresponding quotients are not 2-manifolds, just orbifold
Orbifold
In the mathematical disciplines of topology, geometry, and geometric group theory, an orbifold is a generalization of a manifold...
s.

Hyperbolic geometry


Non-Euclidean geometry
Non-Euclidean geometry is the term used to refer to two specific geometries which are, loosely speaking, obtained by negating the Euclidean parallel postulate, namely hyperbolic and elliptic geometry. This is one term which, for historical reasons, has a meaning in mathematics which is much...
was first discussed in letters of Gauss, who made extensive computations at the turn of the nineteenth century which, although privately circulated, he decided not to put into print. In 1830 Lobachevsky and independently in 1832 Bolyai, the son of one Gauss' correspondents, published synthetic versions of this new geometry, for which they were severely criticized. However it was not until 1868 that Beltrami
Beltrami
Beltrami may refer to:People*Eugenio Beltrami, Italian mathematician*Giacomo Beltrami, Italian count for whom the Minnesota county is named, and who claimed to have discovered the Mississippi River headwaters*Joseph Beltrami, Scottish lawyer...
, followed by Klein
Felix Klein
Christian Felix Klein was a German mathematician, known for his work in group theory, function theory, non-Euclidean geometry, and on the connections between geometry and group theory...
in 1871 and Poincaré
Poincaré
Several members of the French Poincaré family have been successful in public and scientific life:* Henri Poincaré , physicist, mathematician and philosopher of science* Lucien Poincaré , physicist, brother of Raymond and cousin of Henri...
in 1882, gave concrete analytic models for what Klein dubbed hyperbolic geometry
Hyperbolic geometry
In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
. The four models of 2-dimensional hyperbolic geometry that emerged were:
- the Beltrami-Klein model;
- the Poincaré disk;
- the Poincaré upper half-plane;
- the hyperboloid modelHyperboloid modelIn geometry, the hyperboloid model, also known as the Minkowski model or the Lorentz model , is a model of n-dimensional hyperbolic geometry in which points are represented by the points on the forward sheet S+ of a two-sheeted hyperboloid in -dimensional Minkowski space and m-planes are...
of Wilhelm KillingWilhelm KillingWilhelm Karl Joseph Killing was a German mathematician who made important contributions to the theories of Lie algebras, Lie groups, and non-Euclidean geometry....
in 3-dimensional Minkowski spaceMinkowski spaceIn physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
.
The first model, based on a disk, has the advantage that geodesics are actually line segments (that is, intersections of Euclidean lines with the open unit disk).The last model has the advantage that it gives a construction which is completely parallel to that of the unit sphere in 3-dimensional Euclidean space. Because of their application in complex analysis and geometry, however, the models of Poincaré are the most widely used: they are interchangeable thanks to the Möbius transformations between the disk and the upper half-plane.
Let
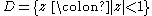
be the Poincaré disk in the complex plane with Poincaré metric
Poincaré metric
In mathematics, the Poincaré metric, named after Henri Poincaré, is the metric tensor describing a two-dimensional surface of constant negative curvature. It is the natural metric commonly used in a variety of calculations in hyperbolic geometry or Riemann surfaces.There are three equivalent...
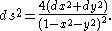
In polar coordinates (r, θ) the metric is given by
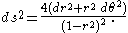
The length of a curve γ:[a,b]
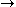 D is given by the formula
D is given by the formula
The group G = SU(1,1) given by
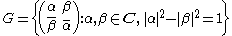
acts transitively by Möbius transformations on D and the stabilizer subgroup of 0 is the rotation group
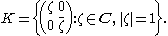
The quotient group SU(1,1)/±I is the group of orientation-preserving isometries of D. Any two points z, w in D are joined by a unique geodesic, given by the portion of the circle or straight line passing through z and w and orthogonal to the boundary circle. The distance between z and w is given by
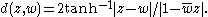
In particular d(0,r) = 2 tanh−1 r and c(t) = tanh t/2 is the geodesic through 0 along the real axis, parametrized by arclength.
The topology defined by this metric is equivalent to the usual Euclidean topology, although as a metric space (D,d) is complete.
A hyperbolic triangle
Hyperbolic triangle
In mathematics, the term hyperbolic triangle has more than one meaning.-Hyperbolic geometry:In hyperbolic geometry, a hyperbolic triangle is a figure in the hyperbolic plane, analogous to a triangle in Euclidean geometry, consisting of three sides and three angles...
is a geodesic triangle for this metric: any three points in D are vertices of a hyperbolic triangle. If the sides have length a, b, c with corresponding angles α, β, γ, then the hyperbolic cosine rule states that
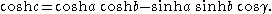
The area of the hyperbolic triangle is given by
- Area = π – α – β – γ.
The unit disk and the upper half-plane
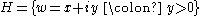
are conformally equivalent by the Möbius transformations
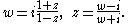
Under this correspondence the action of SL(2,R) by Möbius transformations on H corresponds to that of SU(1,1) on D. The metric on H becomes
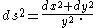
Since lines or circles are preserved under Möbius transformations, geodesics are again described by lines or circles orthogonal to the real axis.
The unit disk with the Poincaré metric is the unique simply connected oriented 2-dimensional Riemannian manifold with constant curvature -1. Any oriented closed surface M with this property has D as its universal covering space. Its fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
can be identified with a torsion-free
concompact subgroup Γ of SU(1,1), in such a way that
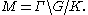
In this case Γ is a finitely presented group. The generators and relations are encoded in a geodesically convex fundamental geodesic polygon in D (or H) corresponding geometrically to closed geodesics on M.
Examples.
- the Bolza surfaceBolza surfaceIn mathematics, the Bolza surface, alternatively, complex algebraic Bolza curve , is a compact Riemann surface of genus 2 with the highest possible order of the conformal automorphism group in this genus, namely 48. An affine model for the Bolza surface can be obtained as the locus of the...
of genus 2; - the Klein quarticKlein quarticIn hyperbolic geometry, the Klein quartic, named after Felix Klein, is a compact Riemann surface of genus 3 with the highest possible order automorphism group for this genus, namely order 168 orientation-preserving automorphisms, and 336 automorphisms if orientation may be reversed...
of genus 3; - the Macbeath surfaceMacbeath surfaceIn Riemann surface theory and hyperbolic geometry, the Macbeath surface, also called Macbeath's curve or the Fricke–Macbeath curve, is the genus-7 Hurwitz surface....
of genus 7; - the First Hurwitz tripletFirst Hurwitz tripletIn the mathematical theory of Riemann surfaces, the first Hurwitz triplet is a triple of distinct Hurwitz surfaces with the identical automorphism group of the lowest possible genus, namely 14 . The explanation for this phenomenon is arithmetic...
of genus 14.
Uniformization
Given an oriented closed surface M with Gaussian curvature K, the metric on M can be changed conformally by scaling it by a factor e2u. The new Gaussian curvature K is then given by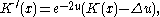
where Δ is the Laplacian for the original metric. Thus to show that a given surface is conformally equivalent to a metric with constant curvature K
it suffices to solve the following variant of Liouville's equation:
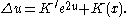
When M has Euler characteristic 0, so is diffeomorphic to a torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
, K = 0, so this amounts to solving
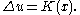
By standard elliptic theory, this is possible because the integral of K over M is zero, by the Gauss-Bonnet theorem.
When M has negative Euler characteristic, K = -1, so the equation to be solved is:
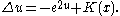
Using the continuity of the exponential map on Sobolev space
Sobolev space
In mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...
due to Neil Trudinger
Neil Trudinger
Neil Sidney Trudinger is an Australian mathematician, known particularly for his work in the field of nonlinear elliptic partial differential equations....
, this non-linear equation can always be solved.
Finally in the case of the 2-sphere, K = 1 and the equation becomes:
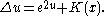
So far this non-linear equation has not been analysed directly, although classical results such as the Riemann-Roch theorem imply that it always has a solution. The method of Ricci flow
Ricci flow
In differential geometry, the Ricci flow is an intrinsic geometric flow. It is a process that deforms the metric of a Riemannian manifold in a way formally analogous to the diffusion of heat, smoothing out irregularities in the metric....
, developed by Richard Hamilton
Richard Hamilton (professor)
Richard Streit Hamilton is Davies Professor of mathematics at Columbia University.He received his B.A in 1963 from Yale University and Ph.D. in 1966 from Princeton University. Robert Gunning supervised his thesis...
, gives another proof of existence based on non-linear partial differential equations to prove existence. In fact the Ricci flow on conformal metrics on S2 is defined on functions u(x, t) by
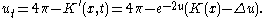
After finite time, Chow showed that K' becomes positive; previous results of Hamilton could then be used to show that K' converges to +1.
A simple proof using only elliptic operators discovered in 1988 can be found in . Let G be the Green's function
Green's function
In mathematics, a Green's function is a type of function used to solve inhomogeneous differential equations subject to specific initial conditions or boundary conditions...
on
S2 satisfying ΔG = 1 + 4πδP, where δP is the point measure at a fixed point P of S2. The equation Δv = 2K – 2, has a smooth solution v, because the right hand side has integral 0 by the Gauss-Bonnet theorem. Thus φ = 2G + v satisfies Δφ = 2K away from P. It follows that g1 = eφg is a complete metric of constant curvature 0 on the complement of P, which is therefore isometric to the plane. Composing with stereographic projection
Stereographic projection
The stereographic projection, in geometry, is a particular mapping that projects a sphere onto a plane. The projection is defined on the entire sphere, except at one point — the projection point. Where it is defined, the mapping is smooth and bijective. It is conformal, meaning that it...
, it follows that there is a smooth function u such that e2ug has Gaussian curvature +1 on the complement of P. The function u automatically extends to a smooth function on the whole of S2.
Surfaces of non-positive curvature
In a region where the curvature of the surface satisfies K≤0, geodesic triangles satisfy the CAT(0)CAT(k) space
In mathematics, a CAT space is a specific type of metric space. Intuitively, triangles in a CAT space are "slimmer" than corresponding "model triangles" in a standard space of constant curvature k. In a CAT space, the curvature is bounded from above by k...
inequalities of comparison geometry, studied by Cartan
Élie Cartan
Élie Joseph Cartan was an influential French mathematician, who did fundamental work in the theory of Lie groups and their geometric applications...
, Alexandrov
Aleksandr Danilovich Aleksandrov
Aleksandr Danilovich Aleksandrov , and Alexandrov ) , was a Soviet/Russian mathematician, physicist, philosopher and mountaineer.- Scientific career :...
and Toponogov
Victor Andreevich Toponogov
Victor Andreevich Toponogov was a Russian mathematician, noted for his contributions to differential geometry and so-called Riemannian geometry "in the large"....
, and considered later from a different point of view by Bruhat
François Bruhat
François Georges René Bruhat was a French mathematician who worked on algebraic groups. The Bruhat order of a Weyl group, the Bruhat decomposition, and the Schwartz–Bruhat functions are named after him....
and Tits
Jacques Tits
Jacques Tits is a Belgian and French mathematician who works on group theory and geometry and who introduced Tits buildings, the Tits alternative, and the Tits group.- Career :Tits received his doctorate in mathematics at the age of 20...
; thanks to the vision of Gromov, this characterisation of non-positive curvature in terms of the underlying metric space has had a profound impact on modern geometry and in particular geometric group theory
Geometric group theory
Geometric group theory is an area in mathematics devoted to the study of finitely generated groups via exploring the connections between algebraic properties of such groups and topological and geometric properties of spaces on which these groups act .Another important...
. Many results known for smooth surfaces and their geodesics, such as Birkhoff's method of constructing geodesics by his curve-shortening process or van Mangoldt and Hadamard's theorem that a simply connected surface of non-positive curvature is homeomorphic to the plane, are equally valid in this more general setting.
Alexandrov's comparison inequality
The simplest form of the comparison inequality, first proved for surfaces by Alexandrov around 1940, states thatThe inequality follows from the fact that if c(t) describes a geodesic parametrised by arclength and a is a fixed point, then
- f(t) = d(a,c(t))2 − t2
is a convex function
Convex function
In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
, i.e.
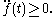
Taking geodesic polar coordinates with origin at a so that ||c(t)|| = r(t), convexity is equivalent to
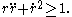
Changing to normal coordinates u, v at c(t), this inequality becomes
- u2 + H − 1 Hr v2 ≥ 1,
where (u,v) corresponds to the unit vector
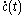 .
.This follows from the inequality Hr ≥ H, a consequence of the non-negativity of the derivative of the Wronskian
Wronskian
In mathematics, the Wronskian is a determinant introduced by and named by . It is used in the study of differential equations, where it can sometimes be used to show that a set of solutions is linearly independent.-Definition:...
of H and r from Sturm–Liouville theory.

Existence of geodesics
On a complete curved surface any two points can be joined by a geodesic. This is a special case of the Hopf-Rinow theorem, which alsoapplies in higher dimensions. The completeness assumption is automatically fulfilled for a surface which is embedded as a closed subset of Euclidean space.
However, it is no longer fulfilled if, for example, we remove an isolated point from a surface. For example, the complement of the origin in the Euclidean plane
is an example of a non-complete surface; in this example two points which are diametrically opposite across the origin cannot be
joined by a geodesic without leaving the punctured plan).
Von Mangoldt-Hadamard theorem
For closed surfaces of non-positive curvature, von MangoldtHans Carl Friedrich von Mangoldt
Hans Carl Friedrich von Mangoldt was a German mathematician who contributed to the solution of the prime number theorem.Von Mangoldt completed his Doctor of Philosophy in 1878 at the University of Berlin, where his advisors were Ernst Kummer and Karl Weierstrass...
(1881) and Hadamard
Jacques Hadamard
Jacques Salomon Hadamard FRS was a French mathematician who made major contributions in number theory, complex function theory, differential geometry and partial differential equations.-Biography:...
(1898) proved that the exponential map at a point is a covering map, so that the universal covering space of the manifold is E². This result was generalised to higher dimensions by Cartan
Élie Cartan
Élie Joseph Cartan was an influential French mathematician, who did fundamental work in the theory of Lie groups and their geometric applications...
and is usually referred to in this form as the Cartan–Hadamard theorem
Cartan–Hadamard theorem
The Cartan–Hadamard theorem is a statement in Riemannian geometry concerning the structure of complete Riemannian manifolds of non-positive sectional curvature. The theorem states that the universal cover of such a manifold is diffeomorphic to a Euclidean space via the exponential map at any point...
. For surfaces, this result follows from three important facts:
- The exponential map has non-zero Jacobian everywhere for non-positively curved surfaces, a consequence of the non-vanishing of Hr.
- Every geodesic is infinitely extendible, a result known as the Hopf-Rinow theorem for n-dimensional manifolds. In two dimensions, if a geodesic tended at infinity towards a point x, a closed disc D centred on a nearby point y with x removed would be contractible to y along geodesics, a topological impossibility.
- Every two points in a homotopy class are connected by a unique geodesic (see above).
Riemannian connection and parallel transport

Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
initiated by Bernhard Riemann
Bernhard Riemann
Georg Friedrich Bernhard Riemann was an influential German mathematician who made lasting contributions to analysis and differential geometry, some of them enabling the later development of general relativity....
in the mid-nineteenth century and of connection
Connection (mathematics)
In geometry, the notion of a connection makes precise the idea of transporting data along a curve or family of curves in a parallel and consistent manner. There are a variety of kinds of connections in modern geometry, depending on what sort of data one wants to transport...
developed by Tullio Levi-Civita
Tullio Levi-Civita
Tullio Levi-Civita, FRS was an Italian mathematician, most famous for his work on absolute differential calculus and its applications to the theory of relativity, but who also made significant contributions in other areas. He was a pupil of Gregorio Ricci-Curbastro, the inventor of tensor calculus...
, Élie Cartan
Élie Cartan
Élie Joseph Cartan was an influential French mathematician, who did fundamental work in the theory of Lie groups and their geometric applications...
and Hermann Weyl
Hermann Weyl
Hermann Klaus Hugo Weyl was a German mathematician and theoretical physicist. Although much of his working life was spent in Zürich, Switzerland and then Princeton, he is associated with the University of Göttingen tradition of mathematics, represented by David Hilbert and Hermann Minkowski.His...
in the early twentieth century. The notion of connection, covariant derivative
Covariant derivative
In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...
and parallel transport
Parallel transport
In geometry, parallel transport is a way of transporting geometrical data along smooth curves in a manifold. If the manifold is equipped with an affine connection , then this connection allows one to transport vectors of the manifold along curves so that they stay parallel with respect to the...
gave a more conceptual and uniform way of understanding curvature, which not only allowed generalisations to higher dimensional manifolds but also provided an important tool for defining new geometric invariants, called characteristic classes. The approach using covariant derivatives and connections is nowadays the one adopted in more advanced textbooks.
Covariant derivative
Connections on a surface can be defined from various equivalent but equally important points of view. The Riemannian connection or Levi-Civita connectionLevi-Civita connection
In Riemannian geometry, the Levi-Civita connection is a specific connection on the tangent bundle of a manifold. More specifically, it is the torsion-free metric connection, i.e., the torsion-free connection on the tangent bundle preserving a given Riemannian metric.The fundamental theorem of...
is perhaps most easily understood in terms of lifting vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
s, considered as first order differential operator
Differential operator
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
s acting on functions on the manifold, to differential operators on the tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
or frame bundle
Frame bundle
In mathematics, a frame bundle is a principal fiber bundle F associated to any vector bundle E. The fiber of F over a point x is the set of all ordered bases, or frames, for Ex...
.
In the case of an embedded surface, the lift to an operator on vector fields, called the covariant derivative, is very simply described in terms of orthogonal projection. Indeed a vector field on a surface embedded in
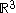 can be regarded as a function from the surface into R3. Another vector field act as a differential operator component-wise. The resulting vector field will not be tangent to the surface, but this can be corrected taking its orthogonal projection onto the tangent space at each point of the surface. As Ricci
can be regarded as a function from the surface into R3. Another vector field act as a differential operator component-wise. The resulting vector field will not be tangent to the surface, but this can be corrected taking its orthogonal projection onto the tangent space at each point of the surface. As RicciRicci
Ricci is an Italian surname, and can also be a shortened version of Riccardo, as a first name and may refer to:-Surname:* Christie Ricci, American wrestler* Christina Ricci, American actress* Fausto Ricci, Italian motorcycle racer...
and Levi-Civita realised at the turn of the twentieth century, this process depends only on the metric and can be locally expressed in terms of the Christoffel symbols.

Parallel transport
Parallel transportParallel transport
In geometry, parallel transport is a way of transporting geometrical data along smooth curves in a manifold. If the manifold is equipped with an affine connection , then this connection allows one to transport vectors of the manifold along curves so that they stay parallel with respect to the...
of tangent vectors along a curve in the surface was the next major advance in the subject, due to Levi-Civita. It is related to the earlier notion of covariant derivative, because it is the monodromy
Monodromy
In mathematics, monodromy is the study of how objects from mathematical analysis, algebraic topology and algebraic and differential geometry behave as they 'run round' a singularity. As the name implies, the fundamental meaning of monodromy comes from 'running round singly'...
of the ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
on the curve defined by the covariant derivative with respect to the velocity vector of the curve. Parallel transport along geodesics, the "straight lines" of the surface, can also easily be described directly. A vector in the tangent plane is transported along a geodesic as the unique vector field with constant length and making a constant angle with the velocity vector of the geodesic. For a general curve, this process has to be modified using the geodesic curvature, which measures how far the curve departs from being a geodesic.
A vector field v(t) along a unit speed curve c(t), with geodesic curvature kg(t), is said to be parallel along the curve if
- it has constant length
- the angle θ(t) that it makes with the velocity vector
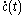 satisfies
satisfies
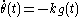
This recaptures the rule for parallel transport along a geodesic or piecewise geodesic curve, because in that case kg = 0, so that the angle θ(t) should remain constant on any geodesic segment. The existence of parallel transport follows because θ(t) can be computed as the integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
of the geodesic curvature. Since it therefore depends continuously on the L2 norm of kg, it follows that parallel transport for an arbitrary curve can be obtained as the limit of the parallel transport on approximating piecewise geodesic curves.
The connection can thus be described in terms of lifting paths in the manifold to paths in the tangent or orthonormal frame bundle, thus formalising the classical theory of the "moving frame
Moving frame
In mathematics, a moving frame is a flexible generalization of the notion of an ordered basis of a vector space often used to study the extrinsic differential geometry of smooth manifolds embedded in a homogeneous space.-Introduction:...
", favoured by French authors. Lifts of loops about a point give rise to the holonomy group at that point. The Gaussian curvature at a point can be recovered from parallel transport around increasingly small loops at the point. Equivalently curvature can be calculated directly at an infinitesimal level in terms of Lie brackets
Lie bracket of vector fields
In the mathematical field of differential topology, the Lie bracket of vector fields, Jacobi–Lie bracket, or commutator of vector fields is a bilinear differential operator which assigns, to any two vector fields X and Y on a smooth manifold M, a third vector field denoted [X, Y]...
of lifted vector fields.

Connection 1-form
The approach of Cartan and Weyl, using connection 1-forms on the frame bundleFrame bundle
In mathematics, a frame bundle is a principal fiber bundle F associated to any vector bundle E. The fiber of F over a point x is the set of all ordered bases, or frames, for Ex...
of M, gives a third way to understand the Riemannian connection.
They noticed that parallel transport dictates that a path in the surface be lifted to a path in the frame bundle so that its tangent vectors lie in a
special subspace of codimension one in the three-dimensional tangent space of the frame bundle. The projection onto this subspace is defined by a differential 1-form on the orthonormal frame bundle, the connection form
Connection form
In mathematics, and specifically differential geometry, a connection form is a manner of organizing the data of a connection using the language of moving frames and differential forms....
. This enabled the curvature properties of the surface to be encoded in differential forms on the frame bundle and formulas involving their exterior derivative
Exterior derivative
In differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
s.
This approach is particularly simple for an embedded surface. Thanks to a result of , the connection 1-form on a surface embedded in Euclidean space E3 is just the pullback under the Gauss map of the connection 1-form on S2. Using the identification of S2 with the homogeneous space
Homogeneous space
In mathematics, particularly in the theories of Lie groups, algebraic groups and topological groups, a homogeneous space for a group G is a non-empty manifold or topological space X on which G acts continuously by symmetry in a transitive way. A special case of this is when the topological group,...
SO(3)/SO(2), the connection 1-form is just a component of the Maurer-Cartan 1-form
Maurer-Cartan form
In mathematics, the Maurer–Cartan form for a Lie group G is a distinguished differential one-form on G that carries the basic infinitesimal information about the structure of G...
on SO(3).
Global differential geometry of surfaces
Although the characterisation of curvature involves only the local geometry of a surface, there are important global aspects such as the Gauss-Bonnet theorem, the uniformization theoremUniformization theorem
In mathematics, the uniformization theorem says that any simply connected Riemann surface is conformally equivalent to one of the three domains: the open unit disk, the complex plane, or the Riemann sphere. In particular it admits a Riemannian metric of constant curvature...
, the von Mangoldt-Hadamard theorem, and the embeddability theorem. There are other important aspects of the global geometry of surfaces. These include:
- Injectivity radius, defined as the largest r such that two points at a distance less than r are joined by a unique geodesic. Wilhelm Klingenberg proved in 1959 that the injectivity radius of a closed surface is bounded below by the minimum of
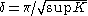 and the length of its smallest closed geodesic. This improved a theorem of Bonnet who showed in 1855 that the diameter of a closed surface of positive Gaussian curvature is always bounded above by δ; in other words a geodesic realising the metric distance between two points cannot have length greater than δ.
and the length of its smallest closed geodesic. This improved a theorem of Bonnet who showed in 1855 that the diameter of a closed surface of positive Gaussian curvature is always bounded above by δ; in other words a geodesic realising the metric distance between two points cannot have length greater than δ.
- Rigidity. In 1927 Cohn-Vossen proved that two ovaloids – closed surfaces with positive Gaussian curvature – that are isometric are necessarily congruent by an isometry of E3. Moreover a closed embedded surface with positive Gaussian curvature and constant mean curvature is necessarily a sphere; likewise a closed embedded curvature of constant Gaussian curvature must be a sphere (Liebmann 1899). Heinz HopfHeinz HopfHeinz Hopf was a German mathematician born in Gräbschen, Germany . He attended Dr. Karl Mittelhaus' higher boys' school from 1901 to 1904, and then entered the König-Wilhelm- Gymnasium in Breslau. He showed mathematical talent from an early age...
showed in 1950 that a closed embedded surface with constant mean curvature and genus 0, i.e. homeomorphic to a sphere, is necessarily a sphere; five years later Alexandrov removed the topological assumption. In the 1980s, Wente constructed immersed tori of constant mean curvature in Euclidean 3-space.
- Carathéodory conjectureCarathéodory conjectureThe Carathéodory conjecture is a mathematical conjecture attributed to Constantin Carathéodory by Hans Ludwig Hamburger in a session of the Berlin Mathematical Society in 1924, [1]. Other early references are the Invited Lecture [3] of Stefan Cohn-Vossen at the International Congress of...
: This conjecture states that a closed convex three times differentiable surface admits at least two umbilic points. The first work on this conjecture was in 1924 by Hans HamburgerHans HamburgerHans Ludwig Hamburger was a German mathematician. He was a professor at universities in Berlin, Cologne and Ankara....
, who noted that it follows from the following stronger claim : the half-integer valued index of the principal curvature foliation of an isolated umbilic is at most one. The contribution of Hamburger and those of subsequent authors to proving this local conjecture are inconclusive.
- Zero Gaussian curvature: a complete surface in E3 with zero Gaussian curvature must be a cylinder or a plane.
- Hilbert's theorem (1901): no complete surface with constant negative curvature can be immersed isometrically in E3.

- The Willmore conjectureWillmore conjectureIn differential geometry in mathematics the Willmore conjecture is a conjecture about the Willmore energy of a torus, named after the English mathematician Tom Willmore.-Statement of the conjecture:...
. This conjecture states that the integral of the square of the mean curvature of a torus immersed in E3 should be bounded below by 2 π2. The conjecture has been proved for large classes of torus immersions. It is also known that the integral is a conformal invariant.
- Isoperimetric inequalities. In 1939 Schmidt proved that the classical isoperimetric inequality for curves in the Euclidean plane is also valid on the sphere or in the hyperbolic plane: namely he showed that among all closed curves bounding a domain of fixed area, the perimeter is minimized by when the curve is a circle for the metric. In one dimension higher, it is known that among all closed surfaces in E3 arising as the boundary of a bounded domain of unit volume, the surface area is minimized for a Euclidean ball.
- Systolic inequalities for curves on surfacesSystoles of surfacesIn mathematics, systolic inequalities for curves on surfaces were first studied by Charles Loewner in 1949 . Given a closed surface, its systole, denoted sys, is defined to the least length of a loop that cannot be contracted to a point on the surface. The systolic area of a metric is defined to...
. Given a closed surface, its systole is defined to be the smallest length of any non-contractible closed curve on the surface. In 1949 Loewner proved a torus inequalityLoewner's torus inequalityIn differential geometry, Loewner's torus inequality is an inequality due to Charles Loewner. It relates the systole and the area of an arbitrary Riemannian metric on the 2-torus.-Statement:...
for metrics on the torus, namely that the area of the torus over the square of its systole is bounded below by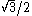 , with equality in the flat (constant curvature) case. A similar result is given by Pu's inequality for the real projective plane from 1952, with a lower bound of 2/π also attained in the constant curvature case. For the Klein bottleKlein bottleIn mathematics, the Klein bottle is a non-orientable surface, informally, a surface in which notions of left and right cannot be consistently defined. Other related non-orientable objects include the Möbius strip and the real projective plane. Whereas a Möbius strip is a surface with boundary, a...
, with equality in the flat (constant curvature) case. A similar result is given by Pu's inequality for the real projective plane from 1952, with a lower bound of 2/π also attained in the constant curvature case. For the Klein bottleKlein bottleIn mathematics, the Klein bottle is a non-orientable surface, informally, a surface in which notions of left and right cannot be consistently defined. Other related non-orientable objects include the Möbius strip and the real projective plane. Whereas a Möbius strip is a surface with boundary, a...
, Blatter and Bavard later obtained a lower bound of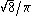 . For a closed surface of genus g, Hebda and Burago showed that the ratio is bounded below by 1/2. Three years later Mikhail Gromov found a lower bound given by a constant times g1/2, although this is not optimal. Asymptotically sharp upper and lower bounds given by constants times g/(log g)2 are due to Gromov and Buser-Sarnak, and can be found in . There is also a version for metrics on the sphere, taking for the systole the length of the smallest closed geodesicClosed geodesicIn differential geometry and dynamical systems, a closed geodesic on a Riemannian manifold M is the projection of a closed orbit of the geodesic flow on M.-Examples:On the unit sphere, every great circle is an example of a closed geodesic...
. For a closed surface of genus g, Hebda and Burago showed that the ratio is bounded below by 1/2. Three years later Mikhail Gromov found a lower bound given by a constant times g1/2, although this is not optimal. Asymptotically sharp upper and lower bounds given by constants times g/(log g)2 are due to Gromov and Buser-Sarnak, and can be found in . There is also a version for metrics on the sphere, taking for the systole the length of the smallest closed geodesicClosed geodesicIn differential geometry and dynamical systems, a closed geodesic on a Riemannian manifold M is the projection of a closed orbit of the geodesic flow on M.-Examples:On the unit sphere, every great circle is an example of a closed geodesic...
. Gromov conjectured a lower bound of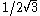 in 1980: the best result so far is the lower bound of 1/8 obtained by Regina Rotman in 2006.
in 1980: the best result so far is the lower bound of 1/8 obtained by Regina Rotman in 2006.
Reading guide
One of the most comprehensive introductory surveys of the subject, charting the historical development from before Gauss to modern times, is by . Accounts of the classical theory are given in , and ; the more modern copiously illustrated undergraduate textbooks by , and might be found more accessible. An accessible account of the classical theory can be found in . More sophisticated graduate-level treatments using the Riemannian connection on a surfaceRiemannian connection on a surface
In mathematics, the Riemannian connection on a surface or Riemannian 2-manifold refers to several intrinsic geometric structures discovered by Tullio Levi-Civita, Élie Cartan and Hermann Weyl in the early part of the twentieth century: parallel transport, covariant derivative and connection form...
can be found in , and .

