Ricci flow
Encyclopedia
In differential geometry, the Ricci flow is an intrinsic geometric flow
. It is a process that deforms the metric of a Riemannian manifold
in a way formally analogous to the diffusion of heat, smoothing out irregularities in the metric
.
The Ricci flow was first introduced by Richard Hamilton in 1981, and is also referred to as the Ricci-Hamilton flow. It is the primary tool used in Grigori Perelman's
solution of the Poincaré conjecture, as well as in the proof of the Differentiable sphere theorem by Brendle and Schoen.
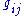, we can compute the Ricci tensor 
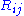, which collects averages of sectional curvatures into a kind of "trace
" of the Riemann curvature tensor
. If we consider the metric tensor (and the associated Ricci tensor) to be functions of a variable which is usually called "time" (but which may have nothing to do with any physical time), then the Ricci flow may be defined by the geometric evolution equation
The normalized Ricci flow makes sense for compact
manifolds and is given by the equation
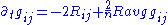
where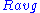
is the average (mean) of the scalar curvature (which is obtained from the Ricci tensor by taking the trace) and 
is the dimension of the manifold. This normalized equation preserves the volume of the metric.
The factor of −2 is of little significance, since it can be changed to any nonzero real number by rescaling t. However the minus sign ensures that the Ricci flow is well defined for sufficiently small positive times; if the sign is changed then the Ricci flow would usually only be defined for small negative times. (This is similar to the way in which the heat equation
can be run forwards in time, but not usually backwards in time.)
Informally, the Ricci flow tends to expand negatively curved regions of the manifold, and contract positively curved regions.
In particular, this shows that in general the Ricci flow cannot be continued for all time, but will produce singularities. For 3 dimensional manifold, Perelman showed how to continue past the singularities using surgery on the manifold.
) was introduced by Richard Hamilton
in 1981 in order to gain insight into the geometrization conjecture
of William Thurston
, which concerns the topological classification
of three-dimensional smooth manifolds. Hamilton's idea was to define a kind of nonlinear diffusion equation
which would tend to smooth out irregularities in the metric. Then, by placing an arbitrary metric g on a given smooth manifold M and evolving the metric by the Ricci flow, the metric should approach a particularly nice metric, which might constitute a canonical form
for M. Suitable canonical forms had already been identified by Thurston; the possibilities, called Thurston model geometries, include the three-sphere S3, three-dimensional Euclidean space E3, three-dimensional hyperbolic space H3, which are homogeneous
and isotropic, and five slightly more exotic Riemannian manifolds, which are homogeneous but not isotropic. (This list is closely related to, but not identical with, the Bianchi classification
of the three-dimensional real Lie algebra
s into nine classes.) Hamilton's idea was that these special metrics should behave like fixed point
s of the Ricci flow, and that if, for a given manifold, globally only one Thurston geometry was admissible, this might even act like an attractor
under the flow.
Hamilton succeeded in proving that any smooth closed three-manifold which admits a metric of positive Ricci curvature also admits a unique Thurston geometry, namely a spherical metric, which does indeed act like an attracting fixed point under the Ricci flow, renormalized to preserve volume. (Under the unrenormalized Ricci flow, the manifold collapses to a point in finite time.) This doesn't prove the full geometrization conjecture because the most difficult case turns out to concern manifolds with negative Ricci curvature and more specifically those with negative sectional curvature. (A strange and interesting fact is that all closed three-manifolds admit metrics with negative Ricci curvatures! This was proved by L. Zhiyong Gao and Shing-Tung Yau in 1986.) Indeed, a triumph of nineteenth century geometry was the proof of the uniformization theorem
, the analogous topological classification of smooth two-manifolds, where Hamilton showed that the Ricci flow does indeed evolve a negatively curved two-manifold into a two-dimensional multi-holed torus which is locally isometric to the hyperbolic plane. This topic is closely related to important topics in analysis, number theory, dynamical systems, mathematical physics, and even cosmology.
Note that the term "uniformization" correctly suggests a kind of smoothing away of irregularities in the geometry, while the term "geometrization" correctly suggests placing a geometry on a smooth manifold. Geometry is being used here in a precise manner akin to Klein
's notion of geometry
(see Geometrization conjecture
for further details). In particular, the result of geometrization may be a geometry that is not isotropic. In most cases including the cases of constant curvature, the geometry is unique. An important theme in this area is the interplay between real and complex formulations. In particular, many discussions of uniformization speak of complex curves rather than real two-manifolds.
The Ricci flow does not preserve volume, so to be more careful in applying the Ricci flow to uniformization and geometrization one needs to normalize the Ricci flow to obtain a flow which preserves volume. If one fail to do this, the problem is that (for example) instead of evolving a given three-dimensional manifold into one of Thurston's canonical forms, we might just shrink its size.
It is possible to construct a kind of moduli space
of n-dimensional Riemannian manifolds, and then the Ricci flow really does give a geometric flow
(in the intuitive sense of particles flowing along flowlines) in this moduli space.
(These coordinates provide an example of a conformal
coordinate chart, because angles, but not distances, are correctly represented.)
The easiest way to compute the Ricci tensor and Laplace-Beltrami operator
for our Riemannian two-manifold is to use the differential forms method of Élie Cartan
. Take the coframe field
so that metric tensor
becomes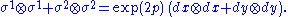
Next, given an arbitrary smooth function
, compute the exterior derivative
Take the Hodge dual
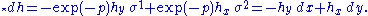
Take another exterior derivative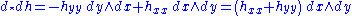
(where we used the anti-commutative property of the exterior product). That is,
Taking another Hodge dual gives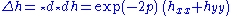
which gives the desired expression for the Laplace/Beltrami operator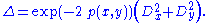
To compute the curvature tensor, we take the exterior derivative of the covector fields making up our coframe: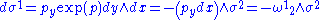
From these expressions, we can read off the only independent connection one-form
Take another exterior derivative
This gives the curvature two-form
from which we can read off the only linearly independent component of the Riemann tensor using
Namely
from which the only nonzero components of the Ricci tensor are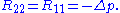
From this, we find components with respect to the coordinate cobasis, namely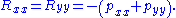
But the metric tensor is also diagonal, with
and after some elementary manipulation, we obtain an elegant expression for the Ricci flow:
This is manifestly analogous to the best known of all diffusion equations, the heat equation
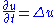
where now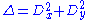
is the usual Laplacian on the Euclidean plane.
The reader may object that the heat equation is of course a linear
partial differential equation
--- where is the promised nonlinearity in the p.d.e. defining the Ricci flow?
The answer is that nonlinearity enters because the Laplace-Beltrami operator depends upon the same function p which we used to define the metric. But notice that the flat Euclidean plane is given by taking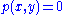
. So if 
is small in magnitude, we can consider it to define small deviations from the geometry of a flat plane, and if we retain only first order terms in computing the exponential, the Ricci flow on our two-dimensional almost flat Riemannian manifold becomes the usual two dimensional heat equation. This computation suggests that, just as (according to the heat equation) an irregular temperature distribution in a hot plate tends to become more homogeneous over time, so too (according to the Ricci flow) an almost flat Riemannian manifold will tend to flatten out the same way that heat can be carried off "to infinity" in an infinite flat plate. But if our hot plate is finite in size, and has no boundary where heat can be carried off, we can expect to homogenize the temperature, but clearly we cannot expect to reduce it to zero. In the same way, we expect that the Ricci flow, applied to a distorted round sphere, will tend to round out the geometry over time, but not to turn it into a flat Euclidean geometry.
may form. For instance, a certain class of solutions to the Ricci flow demonstrates that neckpinch singularities will form on an evolving n-dimensional metric Riemannian manifold having a certain topological property (positive Euler characteristic
), as the flow approaches some characteristic time
. In certain cases, such neckpinches will produce manifolds called Ricci solitons.
There are many related geometric flow
s, some of which (such as the Yamabe flow
and the Calabi flow
) have properties similar to the Ricci flow.
Geometric flow
In mathematics, specifically differential geometry, a geometric flow is the gradient flow associated to a functional on a manifold which has a geometric interpretation, usually associated with some extrinsic or intrinsic curvature...
. It is a process that deforms the metric of a Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
in a way formally analogous to the diffusion of heat, smoothing out irregularities in the metric
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
.
The Ricci flow was first introduced by Richard Hamilton in 1981, and is also referred to as the Ricci-Hamilton flow. It is the primary tool used in Grigori Perelman's
Grigori Perelman
Grigori Yakovlevich Perelman is a Russian mathematician who has made landmark contributions to Riemannian geometry and geometric topology.In 1992, Perelman proved the soul conjecture. In 2002, he proved Thurston's geometrization conjecture...
solution of the Poincaré conjecture, as well as in the proof of the Differentiable sphere theorem by Brendle and Schoen.
Mathematical definition
Given a Riemannian manifold with metric tensorMetric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
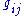, we can compute the Ricci tensor 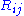, which collects averages of sectional curvatures into a kind of "traceTrace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
" of the Riemann curvature tensor
Riemann curvature tensor
In the mathematical field of differential geometry, the Riemann curvature tensor, or Riemann–Christoffel tensor after Bernhard Riemann and Elwin Bruno Christoffel, is the most standard way to express curvature of Riemannian manifolds...
. If we consider the metric tensor (and the associated Ricci tensor) to be functions of a variable which is usually called "time" (but which may have nothing to do with any physical time), then the Ricci flow may be defined by the geometric evolution equation
The normalized Ricci flow makes sense for compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
manifolds and is given by the equation
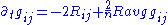
where
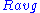is the average (mean) of the scalar curvature (which is obtained from the Ricci tensor by taking the trace) and is the dimension of the manifold. This normalized equation preserves the volume of the metric.The factor of −2 is of little significance, since it can be changed to any nonzero real number by rescaling t. However the minus sign ensures that the Ricci flow is well defined for sufficiently small positive times; if the sign is changed then the Ricci flow would usually only be defined for small negative times. (This is similar to the way in which the heat equation
Heat equation
The heat equation is an important partial differential equation which describes the distribution of heat in a given region over time...
can be run forwards in time, but not usually backwards in time.)
Informally, the Ricci flow tends to expand negatively curved regions of the manifold, and contract positively curved regions.
Examples
- If the manifold is Euclidean space, or more generally Ricci-flatRicci-flat manifoldIn mathematics, Ricci-flat manifolds are Riemannian manifolds whose Ricci curvature vanishes. In physics, they represent vacuum solutions to the analogues of Einstein's equations for Riemannian manifolds of any dimension, with vanishing cosmological constant...
, then Ricci flow leaves the metric unchanged. Conversely, any metric unchanged by Ricci flow is Ricci-flatRicci-flat manifoldIn mathematics, Ricci-flat manifolds are Riemannian manifolds whose Ricci curvature vanishes. In physics, they represent vacuum solutions to the analogues of Einstein's equations for Riemannian manifolds of any dimension, with vanishing cosmological constant...
. - If the manifold is a sphere (with the usual metric) then Ricci flow collapses the manifold to a point in finite time. If the sphere has radius 1 in n dimensions, then after time
the metric will be multiplied by 
, so the manifold will collapse after time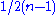 
. More generally, if the manifold is an Einstein manifoldEinstein manifoldIn differential geometry and mathematical physics, an Einstein manifold is a Riemannian or pseudo-Riemannian manifold whose Ricci tensor is proportional to the metric...
(Ricci = constant × metric), then Ricci flow will collapse it to a point if it has positive curvature, leave it invariant if it has zero curvature, and expand it if it has negative curvature. - For a compactCompact spaceIn mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
Einstein manifoldEinstein manifoldIn differential geometry and mathematical physics, an Einstein manifold is a Riemannian or pseudo-Riemannian manifold whose Ricci tensor is proportional to the metric...
, the metric is unchanged under normalized Ricci flow. Conversely, any metric unchanged by normalized Ricci flow is Einstein.
In particular, this shows that in general the Ricci flow cannot be continued for all time, but will produce singularities. For 3 dimensional manifold, Perelman showed how to continue past the singularities using surgery on the manifold.
- A significant 2-dimensional example is the cigar soliton solution, which is given by the metric (dx2 + dy2)/(e4t + x2 + y2) on the Euclidean plane. Although this metric shrinks under the Ricci flow, its geometry remains the same. Such solutions are called steady Ricci solitons. An example of a 3-dimensional steady Ricci soliton is the "Bryant soliton", which is rotationally symmetric, has positive curvature, and is obtained by solving a system of ordinary differential equations.
Relationship to uniformization and geometrization
The Ricci flow (named after Gregorio Ricci-CurbastroGregorio Ricci-Curbastro
Gregorio Ricci-Curbastro was an Italian mathematician. He was born at Lugo di Romagna. He is most famous as the inventor of the tensor calculus but published important work in many fields....
) was introduced by Richard Hamilton
Richard Hamilton (professor)
Richard Streit Hamilton is Davies Professor of mathematics at Columbia University.He received his B.A in 1963 from Yale University and Ph.D. in 1966 from Princeton University. Robert Gunning supervised his thesis...
in 1981 in order to gain insight into the geometrization conjecture
Geometrization conjecture
Thurston's geometrization conjecture states that compact 3-manifolds can be decomposed canonically into submanifolds that have geometric structures. The geometrization conjecture is an analogue for 3-manifolds of the uniformization theorem for surfaces...
of William Thurston
William Thurston
William Paul Thurston is an American mathematician. He is a pioneer in the field of low-dimensional topology. In 1982, he was awarded the Fields Medal for his contributions to the study of 3-manifolds...
, which concerns the topological classification
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
of three-dimensional smooth manifolds. Hamilton's idea was to define a kind of nonlinear diffusion equation
Heat equation
The heat equation is an important partial differential equation which describes the distribution of heat in a given region over time...
which would tend to smooth out irregularities in the metric. Then, by placing an arbitrary metric g on a given smooth manifold M and evolving the metric by the Ricci flow, the metric should approach a particularly nice metric, which might constitute a canonical form
Canonical form
Generally, in mathematics, a canonical form of an object is a standard way of presenting that object....
for M. Suitable canonical forms had already been identified by Thurston; the possibilities, called Thurston model geometries, include the three-sphere S3, three-dimensional Euclidean space E3, three-dimensional hyperbolic space H3, which are homogeneous
Homogeneous space
In mathematics, particularly in the theories of Lie groups, algebraic groups and topological groups, a homogeneous space for a group G is a non-empty manifold or topological space X on which G acts continuously by symmetry in a transitive way. A special case of this is when the topological group,...
and isotropic, and five slightly more exotic Riemannian manifolds, which are homogeneous but not isotropic. (This list is closely related to, but not identical with, the Bianchi classification
Bianchi classification
In mathematics, the Bianchi classification, named for Luigi Bianchi, is a classification of the 3-dimensional real Lie algebras into 11 classes, 9 of which are single groups and two of which have a continuum of isomorphism classes...
of the three-dimensional real Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
s into nine classes.) Hamilton's idea was that these special metrics should behave like fixed point
Fixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
s of the Ricci flow, and that if, for a given manifold, globally only one Thurston geometry was admissible, this might even act like an attractor
Attractor
An attractor is a set towards which a dynamical system evolves over time. That is, points that get close enough to the attractor remain close even if slightly disturbed...
under the flow.
Hamilton succeeded in proving that any smooth closed three-manifold which admits a metric of positive Ricci curvature also admits a unique Thurston geometry, namely a spherical metric, which does indeed act like an attracting fixed point under the Ricci flow, renormalized to preserve volume. (Under the unrenormalized Ricci flow, the manifold collapses to a point in finite time.) This doesn't prove the full geometrization conjecture because the most difficult case turns out to concern manifolds with negative Ricci curvature and more specifically those with negative sectional curvature. (A strange and interesting fact is that all closed three-manifolds admit metrics with negative Ricci curvatures! This was proved by L. Zhiyong Gao and Shing-Tung Yau in 1986.) Indeed, a triumph of nineteenth century geometry was the proof of the uniformization theorem
Uniformization theorem
In mathematics, the uniformization theorem says that any simply connected Riemann surface is conformally equivalent to one of the three domains: the open unit disk, the complex plane, or the Riemann sphere. In particular it admits a Riemannian metric of constant curvature...
, the analogous topological classification of smooth two-manifolds, where Hamilton showed that the Ricci flow does indeed evolve a negatively curved two-manifold into a two-dimensional multi-holed torus which is locally isometric to the hyperbolic plane. This topic is closely related to important topics in analysis, number theory, dynamical systems, mathematical physics, and even cosmology.
Note that the term "uniformization" correctly suggests a kind of smoothing away of irregularities in the geometry, while the term "geometrization" correctly suggests placing a geometry on a smooth manifold. Geometry is being used here in a precise manner akin to Klein
Felix Klein
Christian Felix Klein was a German mathematician, known for his work in group theory, function theory, non-Euclidean geometry, and on the connections between geometry and group theory...
's notion of geometry
Erlangen program
An influential research program and manifesto was published in 1872 by Felix Klein, under the title Vergleichende Betrachtungen über neuere geometrische Forschungen...
(see Geometrization conjecture
Geometrization conjecture
Thurston's geometrization conjecture states that compact 3-manifolds can be decomposed canonically into submanifolds that have geometric structures. The geometrization conjecture is an analogue for 3-manifolds of the uniformization theorem for surfaces...
for further details). In particular, the result of geometrization may be a geometry that is not isotropic. In most cases including the cases of constant curvature, the geometry is unique. An important theme in this area is the interplay between real and complex formulations. In particular, many discussions of uniformization speak of complex curves rather than real two-manifolds.
The Ricci flow does not preserve volume, so to be more careful in applying the Ricci flow to uniformization and geometrization one needs to normalize the Ricci flow to obtain a flow which preserves volume. If one fail to do this, the problem is that (for example) instead of evolving a given three-dimensional manifold into one of Thurston's canonical forms, we might just shrink its size.
It is possible to construct a kind of moduli space
Moduli space
In algebraic geometry, a moduli space is a geometric space whose points represent algebro-geometric objects of some fixed kind, or isomorphism classes of such objects...
of n-dimensional Riemannian manifolds, and then the Ricci flow really does give a geometric flow
Geometric flow
In mathematics, specifically differential geometry, a geometric flow is the gradient flow associated to a functional on a manifold which has a geometric interpretation, usually associated with some extrinsic or intrinsic curvature...
(in the intuitive sense of particles flowing along flowlines) in this moduli space.
Relation to diffusion
To see why the evolution equation defining the Ricci flow is indeed a kind of nonlinear diffusion equation, we can consider the special case of (real) two-manifolds in more detail. Any metric tensor on a two-manifold can be written with respect to an exponential isothermal coordinate chart in the form(These coordinates provide an example of a conformal
Conformal map
In mathematics, a conformal map is a function which preserves angles. In the most common case the function is between domains in the complex plane.More formally, a map,...
coordinate chart, because angles, but not distances, are correctly represented.)
The easiest way to compute the Ricci tensor and Laplace-Beltrami operator
Laplace-Beltrami operator
In differential geometry, the Laplace operator, named after Pierre-Simon Laplace, can be generalized to operate on functions defined on surfaces in Euclidean space and, more generally, on Riemannian and pseudo-Riemannian manifolds. This more general operator goes by the name Laplace–Beltrami...
for our Riemannian two-manifold is to use the differential forms method of Élie Cartan
Élie Cartan
Élie Joseph Cartan was an influential French mathematician, who did fundamental work in the theory of Lie groups and their geometric applications...
. Take the coframe field
so that metric tensor
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
becomes
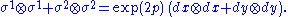
Next, given an arbitrary smooth function
, compute the exterior derivativeExterior derivative
In differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
Take the Hodge dual
Hodge dual
In mathematics, the Hodge star operator or Hodge dual is a significant linear map introduced in general by W. V. D. Hodge. It is defined on the exterior algebra of a finite-dimensional oriented inner product space.-Dimensions and algebra:...
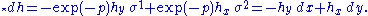
Take another exterior derivative
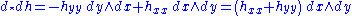
(where we used the anti-commutative property of the exterior product). That is,
Taking another Hodge dual gives
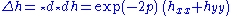
which gives the desired expression for the Laplace/Beltrami operator
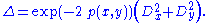
To compute the curvature tensor, we take the exterior derivative of the covector fields making up our coframe:
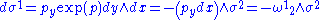
From these expressions, we can read off the only independent connection one-form
Take another exterior derivative
This gives the curvature two-form
from which we can read off the only linearly independent component of the Riemann tensor using
Namely
from which the only nonzero components of the Ricci tensor are
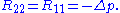
From this, we find components with respect to the coordinate cobasis, namely
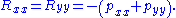
But the metric tensor is also diagonal, with
and after some elementary manipulation, we obtain an elegant expression for the Ricci flow:
This is manifestly analogous to the best known of all diffusion equations, the heat equation
Heat equation
The heat equation is an important partial differential equation which describes the distribution of heat in a given region over time...
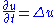
where now
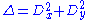is the usual Laplacian on the Euclidean plane.The reader may object that the heat equation is of course a linear
Linear
In mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
--- where is the promised nonlinearity in the p.d.e. defining the Ricci flow?
The answer is that nonlinearity enters because the Laplace-Beltrami operator depends upon the same function p which we used to define the metric. But notice that the flat Euclidean plane is given by taking
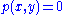. So if is small in magnitude, we can consider it to define small deviations from the geometry of a flat plane, and if we retain only first order terms in computing the exponential, the Ricci flow on our two-dimensional almost flat Riemannian manifold becomes the usual two dimensional heat equation. This computation suggests that, just as (according to the heat equation) an irregular temperature distribution in a hot plate tends to become more homogeneous over time, so too (according to the Ricci flow) an almost flat Riemannian manifold will tend to flatten out the same way that heat can be carried off "to infinity" in an infinite flat plate. But if our hot plate is finite in size, and has no boundary where heat can be carried off, we can expect to homogenize the temperature, but clearly we cannot expect to reduce it to zero. In the same way, we expect that the Ricci flow, applied to a distorted round sphere, will tend to round out the geometry over time, but not to turn it into a flat Euclidean geometry.Recent developments
The Ricci flow has been intensively studied since 1981. Some recent work has focused on the question of precisely how higher-dimensional Riemannian manifolds evolve under the Ricci flow, and in particular, what types of parametric singularitiesMathematical singularity
In mathematics, a singularity is in general a point at which a given mathematical object is not defined, or a point of an exceptional set where it fails to be well-behaved in some particular way, such as differentiability...
may form. For instance, a certain class of solutions to the Ricci flow demonstrates that neckpinch singularities will form on an evolving n-dimensional metric Riemannian manifold having a certain topological property (positive Euler characteristic
Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
), as the flow approaches some characteristic time
. In certain cases, such neckpinches will produce manifolds called Ricci solitons.There are many related geometric flow
Geometric flow
In mathematics, specifically differential geometry, a geometric flow is the gradient flow associated to a functional on a manifold which has a geometric interpretation, usually associated with some extrinsic or intrinsic curvature...
s, some of which (such as the Yamabe flow
Yamabe flow
In differential geometry, the Yamabe flow is an intrinsic geometric flow—a process which deforms the metric of a Riemannian manifold.It is the negative L2-gradient flow of the total scalar curvature, restricted to a given conformal class: it can be interpreted as deforming a Riemannian metric to a...
and the Calabi flow
Calabi flow
In differential geometry, the Calabi flow is an intrinsic geometric flow—a process which deforms the metric of a Riemannian manifold—in a manner formally analogous to the way that vibrations are damped and dissipated in a hypothetical curved n-dimensional structural element.The Calabi flow is an...
) have properties similar to the Ricci flow.
Applications
- uniformization theoremUniformization theoremIn mathematics, the uniformization theorem says that any simply connected Riemann surface is conformally equivalent to one of the three domains: the open unit disk, the complex plane, or the Riemann sphere. In particular it admits a Riemannian metric of constant curvature...
- geometrization conjectureGeometrization conjectureThurston's geometrization conjecture states that compact 3-manifolds can be decomposed canonically into submanifolds that have geometric structures. The geometrization conjecture is an analogue for 3-manifolds of the uniformization theorem for surfaces...
- Solution of the Poincaré conjecture
- Differentiable sphere theorem