Moduli space
Encyclopedia
In algebraic geometry
, a moduli space is a geometric space (usually a scheme
or an algebraic stack) whose points represent algebro-geometric objects of some fixed kind, or isomorphism classes of such objects. Such spaces frequently arise as solutions to classification problems: If one can show that a collection of interesting objects (e.g., the smooth algebraic curves of a fixed genus) can be given the structure of a geometric space, then one can parametrize such objects by introducing coordinates on the resulting space. In this context, the term "modulus" is used synonymously with "parameter"; moduli spaces were first understood as spaces of parameters rather than as spaces of objects.
Pn is a moduli space. It is the space of lines in Rn+1 which pass through the origin. Similarly, complex projective space is the space of all complex lines in Cn+1 passing through the origin.
More generally, the Grassmannian
G(k, V) of a vector space V over a field F is the moduli space of all k-dimensional linear subspaces of V.
Hilb(X) is a moduli scheme. Every closed point of Hilb(X) corresponds to a closed subscheme of a fixed scheme X, and every closed subscheme is represented by such a point.
of U along a unique map B → M. A fine moduli space is a space M which is the base of a universal family.
More precisely, suppose that we have a functor F from schemes to sets, which assigns to a scheme B the set of all suitable families of objects with base B. A space M is a fine moduli space for the functor F if M represents
F, i.e., the functor of points Hom(−,M) is naturally isomorphic to F. This implies that M carries a universal family; this family is the family on M corresponding to the identity map 1M ∈ Hom(M, M).
In other words, a fine moduli space includes both a base space M and universal family T → M, while a coarse moduli space only has the base space M.
s. This in particular makes the existence of a fine moduli space impossible (intuitively, the idea is that if L is some geometric object, the trivial family L × [0,1] can be made into a twisted family on the circle S1 by identifying L × {0} with L × {1} via a nontrivial automorphism. Now if a fine moduli space X existed, the map S1 → X should not be constant, but would have to be constant on any proper open set by triviality), one can still sometimes obtain a coarse moduli space. However, this approach is not ideal, as such spaces are not guaranteed to exist, are frequently singular when they do exist, and miss details about some non-trivial families of objects they classify.
A more sophisticated approach is to enrich the classification by remembering the isomorphisms. More precisely, on any base B one can consider the category of families on B with only isomorphisms between families taken as morphisms. One then considers the fibred category
which assigns to any space B the groupoid of families over B. The use of these categories fibred in groupoids to describe a moduli problem goes back to Grothendieck (1960/61). In general they cannot be represented by schemes or even algebraic space
s, but in many cases they have a natural structure of an algebraic stack.
Algebraic stacks and their use to analyse moduli problems appeared in Deligne-Mumford (1969) as a tool to prove the irreducibility of the (coarse) moduli space of curves of a given genus. The language of algebraic stacks essentially provides a systematic way to view the fibred category that constitutes the moduli problem as a "space", and the moduli stack of many moduli problems is better-behaved (such as smooth) than the corresponding coarse moduli space.
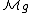classifies families of smooth projective curves of genus 
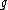, together with their isomorphisms. When g > 1, this stack may be compactified by adding new "boundary" points which correspond to stable nodal curves (together with their isomorphisms). A curve is stable if it has only a finite group of automorphisms. The resulting stack is denoted 
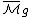. Both moduli stacks carry universal families of curves. One can also define coarse moduli spaces representing isomorphism classes of smooth or stable curves. These coarse moduli spaces were actually studied before the notion of moduli stack was invented. In fact, the idea of a moduli stack was invented by Deligne and Mumford in an attempt to prove the projectivity of the coarse moduli spaces. In recent years, it has become apparent that the stack of curves is actually the more fundamental object.
Both stacks above have dimension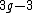
; hence a stable nodal curve can be completely specified by choosing the values of 3g-3 parameters, when g > 1. In lower genus, one must account for the presence of smooth families of automorphisms, by subtracting their number. There is exactly one complex curve of genus zero, the Riemann sphere, and its group of isomorphisms is PGL(2). Hence the dimension of 
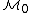is
Likewise, in genus 1, there is a one-dimensional space of curves, but every such curve has a one-dimensional group of automorphisms. Hence the stack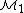
has dimension 0. The coarse moduli spaces have the same dimension as the stacks when g > 1; however, in genus zero the coarse moduli space has dimension zero, and in genus one, it has dimension one.
One can also enrich the problem by considering the moduli stack of genus g nodal curves with n marked points. Such marked curves are said to be stable if the subgroup of curve automorphisms which fix the marked points is finite. The resulting moduli stacks of smooth (or stable) genus g curves with n-marked points are denoted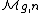
(or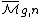 
), and have dimension 3g-3 + n.
A case of particular interest is the moduli stack
of genus 1 curves with one marked point. This is the stack of elliptic curve
s, and is the natural home of the much studied modular form
s, which are meromorphic sections of bundles on this stack.
theory. See also Shimura variety
.
of rank n vector bundle
s on a fixed algebraic variety
X. This stack has been most studied when X is one-dimensional, and especially when n equals one. In this case, the coarse moduli space is the Picard scheme, which like the moduli space of curves, was studied before stacks were invented. Finally, when the bundles have rank 1 and degree zero, the study of the coarse moduli space is the study of the Jacobian variety
.
In applications to physics
, the number of moduli of vector bundles and the closely related problem of the number of moduli of principal G-bundles
has been found to be significant in gauge theory
.
in groupoid
s), and spaces (almost) representing them, dates back to Grothendieck (1960/61), in which he described the general framework, approaches and main problems using Teichmüller space
s in complex analytical geometry as an example. The talks in particular describe the general method of constructing moduli spaces by first rigidifying the moduli problem under consideration.
More precisely, the existence of non-trivial automorphisms of the objects being classified makes it impossible to have a fine moduli space. However, it is often possible to consider a modified moduli problem of classifying the original objects together with additional data, chosen in such a way that the identity is the only automorphism respecting also the additional data. With a suitable choice of the rigidifying data, the modified moduli problem will have a (fine) moduli space T, often described as a subscheme of a suitable Hilbert scheme
or Quot scheme. The rigidifying data is moreover chosen so that it corresponds to a principal bundle with an algebraic structure group G. Thus one can move back from the rigidified problem to the original by taking quotient by the action of G, and the problem of constructing the moduli space becomes that of finding a scheme (or more general space) that is (in a suitably strong sense) the quotient T/G of T by the action of G. The last problem in general does not admit a solution; however, it is addressed by the groundbreaking geometric invariant theory
(GIT), developed by David Mumford
in Mumford (1965), which shows that under suitable conditions the quotient indeed exists.
To see how this might work, consider the problem of parametrizing smooth curves of genus g > 2. A smooth curve together with a complete linear system of degree d > 2g is equivalent to a closed one complex dimensional subscheme of the projective space Pd − g. Consequently, the moduli space of smooth curves and linear systems (satisfying certain criteria) may be embedded in the Hilbert scheme of a sufficiently high-dimensional projective space. This locus H in the Hilbert scheme has an action of PGL(n) which mixes the elements of the linear system; consequently, the moduli space of smooth curves is then recovered as the quotient of H by the projective general linear group.
Another general approach is primarily associated with Michael Artin
. Here the idea is to start with any object of the kind to be classified and study its deformation theory
. This means first constructing infinitesimal
deformations, then appealing to prorepresentability theorems to put these together into an object over a formal
base. Next an appeal to Grothendieck's formal existence theorem provides an object of the desired kind over a base which is a complete local ring. This object can be approximated via Artin's approximation theorem by an object defined over a finitely generated ring. The spectrum
of this latter ring can then be viewed as giving a kind of coordinate chart on the desired moduli space. By gluing together enough of these charts, we can cover the space, but the map from our union of spectra to the moduli space will in general be many to one. We therefore define an equivalence relation
on the former; essentially, two points are equivalent if the objects over each are isomorphic. This gives a scheme
and an equivalence relation, which is enough to define an algebraic space
(actually an algebraic stack if we are being careful) if not always a scheme.
to refer specifically the moduli space of vacuum expectation values of a set of scalar fields, or to the moduli space of possible string background
s.
Moduli spaces also appear in physics in cohomological field theory, where one can use Feynman path integrals to compute the intersection number
s of various algebraic moduli spaces.
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, a moduli space is a geometric space (usually a scheme
Scheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
or an algebraic stack) whose points represent algebro-geometric objects of some fixed kind, or isomorphism classes of such objects. Such spaces frequently arise as solutions to classification problems: If one can show that a collection of interesting objects (e.g., the smooth algebraic curves of a fixed genus) can be given the structure of a geometric space, then one can parametrize such objects by introducing coordinates on the resulting space. In this context, the term "modulus" is used synonymously with "parameter"; moduli spaces were first understood as spaces of parameters rather than as spaces of objects.
Projective Space and Grassmanians
The real projective spaceProjective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
Pn is a moduli space. It is the space of lines in Rn+1 which pass through the origin. Similarly, complex projective space is the space of all complex lines in Cn+1 passing through the origin.
More generally, the Grassmannian
Grassmannian
In mathematics, a Grassmannian is a space which parameterizes all linear subspaces of a vector space V of a given dimension. For example, the Grassmannian Gr is the space of lines through the origin in V, so it is the same as the projective space P. The Grassmanians are compact, topological...
G(k, V) of a vector space V over a field F is the moduli space of all k-dimensional linear subspaces of V.
Hilbert Scheme
The Hilbert schemeHilbert scheme
In algebraic geometry, a branch of mathematics, a Hilbert scheme is a scheme that is the parameter space for the closed subschemes of some projective space , refining the Chow variety. The Hilbert scheme is a disjoint union of projective subschemes corresponding to Hilbert polynomials...
Hilb(X) is a moduli scheme. Every closed point of Hilb(X) corresponds to a closed subscheme of a fixed scheme X, and every closed subscheme is represented by such a point.
Definitions
There are several different related notions of what it means for a space M to be a moduli space. Each of these definitions formalizes a different notion of what it means for the points of a space to represent geometric objects.Fine Moduli Spaces
This is the most important notion. Heuristically, if we have a space M for which each point m∈ M corresponds to an algebro-geometric object Um, then we can assemble these objects into a tautological family U over M. (For example, the Grassmanian G(k, V) carries a rank k bundle whose fiber at any point [L] ∈ G(k, V) is simply the linear subspace L ⊂ V.) We say that such a family is universal if any family of algebro-geometric objects T over any base space B is the pullbackPullback (category theory)
In category theory, a branch of mathematics, a pullback is the limit of a diagram consisting of two morphisms f : X → Z and g : Y → Z with a common codomain; it is the limit of the cospan X \rightarrow Z \leftarrow Y...
of U along a unique map B → M. A fine moduli space is a space M which is the base of a universal family.
More precisely, suppose that we have a functor F from schemes to sets, which assigns to a scheme B the set of all suitable families of objects with base B. A space M is a fine moduli space for the functor F if M represents
Representable functor
In mathematics, particularly category theory, a representable functor is a functor of a special form from an arbitrary category into the category of sets. Such functors give representations of an abstract category in terms of known structures In mathematics, particularly category theory, a...
F, i.e., the functor of points Hom(−,M) is naturally isomorphic to F. This implies that M carries a universal family; this family is the family on M corresponding to the identity map 1M ∈ Hom(M, M).
Coarse Moduli Spaces
Fine moduli spaces are very useful, but they do not always exist and are frequently difficult to construct, so mathematicians sometimes use a weaker notion, the idea of a coarse moduli space. A space M is a coarse moduli space for the functor F if there exists a natural transformation τ: F → Hom(−,M) and τ is universal among such natural transformations. More concretely, M is a coarse moduli space for F if any family T over a base B gives rise to a map φT: B → M and any two objects V and W (regarded as families over a point) correspond to the same point of M if and only if V and W are isomorphic. Thus, M is a space which has a point for every object that could appear in a family, and whose geometry reflects the ways objects can vary in families. Note, however, that a coarse moduli space does not necessarily carry any family of appropriate objects, let alone a universal one.In other words, a fine moduli space includes both a base space M and universal family T → M, while a coarse moduli space only has the base space M.
Moduli stacks
It is frequently the case that interesting geometric objects come equipped with lots of natural automorphismAutomorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
s. This in particular makes the existence of a fine moduli space impossible (intuitively, the idea is that if L is some geometric object, the trivial family L × [0,1] can be made into a twisted family on the circle S1 by identifying L × {0} with L × {1} via a nontrivial automorphism. Now if a fine moduli space X existed, the map S1 → X should not be constant, but would have to be constant on any proper open set by triviality), one can still sometimes obtain a coarse moduli space. However, this approach is not ideal, as such spaces are not guaranteed to exist, are frequently singular when they do exist, and miss details about some non-trivial families of objects they classify.
A more sophisticated approach is to enrich the classification by remembering the isomorphisms. More precisely, on any base B one can consider the category of families on B with only isomorphisms between families taken as morphisms. One then considers the fibred category
Fibred category
Fibred categories are abstract entities in mathematics used to provide a general framework for descent theory. They formalise the various situations in geometry and algebra in which inverse images of objects such as vector bundles can be defined...
which assigns to any space B the groupoid of families over B. The use of these categories fibred in groupoids to describe a moduli problem goes back to Grothendieck (1960/61). In general they cannot be represented by schemes or even algebraic space
Algebraic space
In mathematics, an algebraic space is a generalization of the schemes of algebraic geometry introduced by Michael Artin for use in deformation theory...
s, but in many cases they have a natural structure of an algebraic stack.
Algebraic stacks and their use to analyse moduli problems appeared in Deligne-Mumford (1969) as a tool to prove the irreducibility of the (coarse) moduli space of curves of a given genus. The language of algebraic stacks essentially provides a systematic way to view the fibred category that constitutes the moduli problem as a "space", and the moduli stack of many moduli problems is better-behaved (such as smooth) than the corresponding coarse moduli space.
Moduli of curves
The moduli stack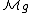 classifies families of smooth projective curves of genus 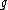, together with their isomorphisms. When g > 1, this stack may be compactified by adding new "boundary" points which correspond to stable nodal curves (together with their isomorphisms). A curve is stable if it has only a finite group of automorphisms. The resulting stack is denoted 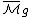. Both moduli stacks carry universal families of curves. One can also define coarse moduli spaces representing isomorphism classes of smooth or stable curves. These coarse moduli spaces were actually studied before the notion of moduli stack was invented. In fact, the idea of a moduli stack was invented by Deligne and Mumford in an attempt to prove the projectivity of the coarse moduli spaces. In recent years, it has become apparent that the stack of curves is actually the more fundamental object.Both stacks above have dimension
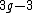; hence a stable nodal curve can be completely specified by choosing the values of 3g-3 parameters, when g > 1. In lower genus, one must account for the presence of smooth families of automorphisms, by subtracting their number. There is exactly one complex curve of genus zero, the Riemann sphere, and its group of isomorphisms is PGL(2). Hence the dimension of 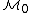is- dim(space of genus zero curves) - dim(group of automorphisms) = 0 - dim(PGL(2)) = -3.
Likewise, in genus 1, there is a one-dimensional space of curves, but every such curve has a one-dimensional group of automorphisms. Hence the stack
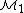has dimension 0. The coarse moduli spaces have the same dimension as the stacks when g > 1; however, in genus zero the coarse moduli space has dimension zero, and in genus one, it has dimension one.One can also enrich the problem by considering the moduli stack of genus g nodal curves with n marked points. Such marked curves are said to be stable if the subgroup of curve automorphisms which fix the marked points is finite. The resulting moduli stacks of smooth (or stable) genus g curves with n-marked points are denoted
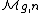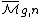(or ), and have dimension 3g-3 + n.A case of particular interest is the moduli stack
of genus 1 curves with one marked point. This is the stack of elliptic curveElliptic curve
In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
s, and is the natural home of the much studied modular form
Modular form
In mathematics, a modular form is a analytic function on the upper half-plane satisfying a certain kind of functional equation and growth condition. The theory of modular forms therefore belongs to complex analysis but the main importance of the theory has traditionally been in its connections...
s, which are meromorphic sections of bundles on this stack.
Moduli of varieties
In higher dimensions, moduli of algebraic varieties are more difficult to construct and study. For instance, the higher dimensional analogue of the moduli space of elliptic curves discussed above is the moduli space of abelian varieties. This is the problem underlying Siegel modular formSiegel modular form
In mathematics, Siegel modular forms are a major type of automorphic form. These stand in relation to the conventional elliptic modular forms as abelian varieties do in relation to elliptic curves; the complex manifolds constructed as in the theory are basic models for what a moduli space for...
theory. See also Shimura variety
Shimura variety
In number theory, a Shimura variety is a higher-dimensional analogue of a modular curve that arises as a quotient of a Hermitian symmetric space by a congruence subgroup of a reductive algebraic group defined over Q. The term "Shimura variety" applies to the higher-dimensional case, in the case of...
.
Moduli of vector bundles
Another important moduli problem is to understand the geometry of (various substacks of) the moduli stack of rank n vector bundleVector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
s on a fixed algebraic variety
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
X. This stack has been most studied when X is one-dimensional, and especially when n equals one. In this case, the coarse moduli space is the Picard scheme, which like the moduli space of curves, was studied before stacks were invented. Finally, when the bundles have rank 1 and degree zero, the study of the coarse moduli space is the study of the Jacobian variety
Jacobian variety
In mathematics, the Jacobian variety J of a non-singular algebraic curve C of genus g is the moduli space of degree 0 line bundles...
.
In applications to physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, the number of moduli of vector bundles and the closely related problem of the number of moduli of principal G-bundles
Fiber bundle
In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
has been found to be significant in gauge theory
Gauge theory
In physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...
.
Methods for constructing moduli spaces
The modern formulation of moduli problems and definition of moduli spaces in terms of the moduli functors (or more generally the categories fibredFibred category
Fibred categories are abstract entities in mathematics used to provide a general framework for descent theory. They formalise the various situations in geometry and algebra in which inverse images of objects such as vector bundles can be defined...
in groupoid
Groupoid
In mathematics, especially in category theory and homotopy theory, a groupoid generalises the notion of group in several equivalent ways. A groupoid can be seen as a:...
s), and spaces (almost) representing them, dates back to Grothendieck (1960/61), in which he described the general framework, approaches and main problems using Teichmüller space
Teichmüller space
In mathematics, the Teichmüller space TX of a topological surface X, is a space that parameterizes complex structures on X up to the action of homeomorphisms that are isotopic to the identity homeomorphism...
s in complex analytical geometry as an example. The talks in particular describe the general method of constructing moduli spaces by first rigidifying the moduli problem under consideration.
More precisely, the existence of non-trivial automorphisms of the objects being classified makes it impossible to have a fine moduli space. However, it is often possible to consider a modified moduli problem of classifying the original objects together with additional data, chosen in such a way that the identity is the only automorphism respecting also the additional data. With a suitable choice of the rigidifying data, the modified moduli problem will have a (fine) moduli space T, often described as a subscheme of a suitable Hilbert scheme
Hilbert scheme
In algebraic geometry, a branch of mathematics, a Hilbert scheme is a scheme that is the parameter space for the closed subschemes of some projective space , refining the Chow variety. The Hilbert scheme is a disjoint union of projective subschemes corresponding to Hilbert polynomials...
or Quot scheme. The rigidifying data is moreover chosen so that it corresponds to a principal bundle with an algebraic structure group G. Thus one can move back from the rigidified problem to the original by taking quotient by the action of G, and the problem of constructing the moduli space becomes that of finding a scheme (or more general space) that is (in a suitably strong sense) the quotient T/G of T by the action of G. The last problem in general does not admit a solution; however, it is addressed by the groundbreaking geometric invariant theory
Geometric invariant theory
In mathematics Geometric invariant theory is a method for constructing quotients by group actions in algebraic geometry, used to construct moduli spaces...
(GIT), developed by David Mumford
David Mumford
David Bryant Mumford is an American mathematician known for distinguished work in algebraic geometry, and then for research into vision and pattern theory. He won the Fields Medal and was a MacArthur Fellow. In 2010 he was awarded the National Medal of Science...
in Mumford (1965), which shows that under suitable conditions the quotient indeed exists.
To see how this might work, consider the problem of parametrizing smooth curves of genus g > 2. A smooth curve together with a complete linear system of degree d > 2g is equivalent to a closed one complex dimensional subscheme of the projective space Pd − g. Consequently, the moduli space of smooth curves and linear systems (satisfying certain criteria) may be embedded in the Hilbert scheme of a sufficiently high-dimensional projective space. This locus H in the Hilbert scheme has an action of PGL(n) which mixes the elements of the linear system; consequently, the moduli space of smooth curves is then recovered as the quotient of H by the projective general linear group.
Another general approach is primarily associated with Michael Artin
Michael Artin
Michael Artin is an American mathematician and a professor emeritus in the Massachusetts Institute of Technology mathematics department, known for his contributions to algebraic geometry. and also generally recognized as one of the outstanding professors in his field.Artin was born in Hamburg,...
. Here the idea is to start with any object of the kind to be classified and study its deformation theory
Deformation theory
In mathematics, deformation theory is the study of infinitesimal conditions associated with varying a solution P of a problem to slightly different solutions Pε, where ε is a small number, or vector of small quantities. The infinitesimal conditions are therefore the result of applying the approach...
. This means first constructing infinitesimal
Infinitesimal
Infinitesimals have been used to express the idea of objects so small that there is no way to see them or to measure them. The word infinitesimal comes from a 17th century Modern Latin coinage infinitesimus, which originally referred to the "infinite-th" item in a series.In common speech, an...
deformations, then appealing to prorepresentability theorems to put these together into an object over a formal
Formal scheme
In mathematics, specifically in algebraic geometry, a formal scheme is a type of space which includes data about its surroundings. Unlike an ordinary scheme, a formal scheme includes infinitesimal data that, in effect, points in a direction off of the scheme...
base. Next an appeal to Grothendieck's formal existence theorem provides an object of the desired kind over a base which is a complete local ring. This object can be approximated via Artin's approximation theorem by an object defined over a finitely generated ring. The spectrum
Spectrum of a ring
In abstract algebra and algebraic geometry, the spectrum of a commutative ring R, denoted by Spec, is the set of all proper prime ideals of R...
of this latter ring can then be viewed as giving a kind of coordinate chart on the desired moduli space. By gluing together enough of these charts, we can cover the space, but the map from our union of spectra to the moduli space will in general be many to one. We therefore define an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
on the former; essentially, two points are equivalent if the objects over each are isomorphic. This gives a scheme
Scheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
and an equivalence relation, which is enough to define an algebraic space
Algebraic space
In mathematics, an algebraic space is a generalization of the schemes of algebraic geometry introduced by Michael Artin for use in deformation theory...
(actually an algebraic stack if we are being careful) if not always a scheme.
In Physics
The term moduli space is sometimes used in physicsPhysics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
to refer specifically the moduli space of vacuum expectation values of a set of scalar fields, or to the moduli space of possible string background
String background
In theoretical physics, a string background refers to the set of classical values of quantum fields in spacetime that correspond to classical solutions of string theory. Such a background is associated with geometry that solves Einstein's equations or their generalizations and with the values of...
s.
Moduli spaces also appear in physics in cohomological field theory, where one can use Feynman path integrals to compute the intersection number
Intersection number
In mathematics, and especially in algebraic geometry, the intersection number generalizes the intuitive notion of counting the number of times two curves intersect to higher dimensions, multiple curves, and accounting properly for tangency...
s of various algebraic moduli spaces.