Eigenvalue, eigenvector and eigenspace

The eigenvectors of a square matrix are the non-zero vectors that, after being multiplied

Matrix multiplication

In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...

by the matrix, remain parallel

Parallel (geometry)

Parallelism is a term in geometry and in everyday life that refers to a property in Euclidean space of two or more lines or planes, or a combination of these. The assumed existence and properties of parallel lines are the basis of Euclid's parallel postulate. Two lines in a plane that do not...

to the original vector. For each eigenvector, the corresponding eigenvalue is the factor by which the eigenvector is scaled when multiplied by the matrix. The prefix eigen- is adopted from the German

German language

German is a West Germanic language, related to and classified alongside English and Dutch. With an estimated 90 – 98 million native speakers, German is one of the world's major languages and is the most widely-spoken first language in the European Union....

word "eigen" for "own" in the sense of a characteristic description. The eigenvectors are sometimes also called characteristic vectors. Similarly, the eigenvalues are also known as characteristic values.

The mathematical expression of this idea is as follows: if A is a square matrix, a non-zero vector v is an eigenvector of A if there is a scalar

Scalar (mathematics)

In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....

λ (lambda) such that

The scalar λ (lambda) is said to be the eigenvalue of A corresponding to v. An eigenspace of A is the set of all eigenvectors with the same eigenvalue together with the zero vector. However, the zero vector is not an eigenvector.

These ideas often are extended to more general situations, where scalars are elements of any field

Field (mathematics)

In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...

, vectors are elements of any vector space, and linear transformations may or may not be represented by matrix multiplication. For example, instead of real numbers, scalars may be complex numbers; instead of arrows, vectors may be functions

Function (mathematics)

In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...

or frequencies

Frequency

Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...

; instead of matrix multiplication, linear transformations may be operators such as the derivative from calculus

Calculus

Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...

. These are only a few of countless examples where eigenvectors and eigenvalues are important.

In such cases, the concept of direction loses its ordinary meaning, and is given an abstract definition. Even so, if that abstract direction is unchanged by a given linear transformation, the prefix "eigen" is used, as in eigenfunction
Eigenfunction
In mathematics, an eigenfunction of a linear operator, A, defined on some function space is any non-zero function f in that space that returns from the operator exactly as is, except for a multiplicative scaling factor. More precisely, one has...

, eigenmode, eigenface
Eigenface
Eigenfaces are a set of eigenvectors used in the computer vision problem of human face recognition. The approach of using eigenfaces for recognition was developed by Sirovich and Kirby and used by Matthew Turk and Alex Pentland in face classification. It is considered the first successful example...

, eigenstate, and eigenfrequency.

Eigenvalues and eigenvectors have many applications in both pure and applied mathematics. They are used in matrix factorization, in quantum mechanics

Quantum mechanics

Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...

, and in many other areas.

Prerequisites and motivation

Eigenvectors and eigenvalues depend on the concepts of vector

Linear algebra

Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...

s and linear transformation

Linear transformation

In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...

s. In the most elementary case, vectors can be thought of as arrows that have both length (or magnitude) and direction

Orientation (geometry)

In geometry the orientation, angular position, or attitude of an object such as a line, plane or rigid body is part of the description of how it is placed in the space it is in....

. Once a set of Cartesian coordinates is established, a vector can be described relative to that set of coordinates by a sequence of numbers. A linear transformation can be described by a square matrix. For example, in the standard coordinates of n-dimensional space, a vector can be written

A matrix can be written

Here n is a fixed natural number

Natural number

In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...

.

Usually, the multiplication

Matrix multiplication

of a vector x by a square matrix A changes both the magnitude and the direction of the vector it acts on—but in the special case where it changes only the scale (magnitude) of the vector and leaves the direction unchanged, or switches the vector to the opposite direction, that vector is called an eigenvector of that matrix. (The term "eigenvector" is meaningless except in relation to some particular matrix.) When multiplied by a matrix, each eigenvector of that matrix changes its magnitude by a factor, called the eigenvalue corresponding to that eigenvector.

The vector x is an eigenvector of the matrix A with eigenvalue λ (lambda) if the following equation holds:

This equation can be interpreted geometrically as follows: a vector x is an eigenvector if multiplication by A stretches, shrinks, leaves unchanged, flips (points in the opposite direction), flips and stretches, or flips and shrinks x. If the eigenvalue , x is stretched by this factor. If λ = 1, the vector x is not affected at all by multiplication by A. If , x is shrunk (or compressed). The case λ = 0 means that x shrinks to a point (represented by the origin

Origin (mathematics)

In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry of the surrounding space. In a Cartesian coordinate system, the origin is the point where the axes of the system intersect...

), meaning that x is in the kernel of the linear map given by A. If then x flips and points in the opposite direction as well as being scaled by a factor equal to the absolute value of λ.

As a special case, the identity matrix

Identity matrix

In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...

I is the matrix that leaves all vectors unchanged:

Every non-zero vector x is an eigenvector of the identity matrix with eigenvalue 1.

Example

For the matrix A

the vector

is an eigenvector with eigenvalue 1. Indeed,

On the other hand the vector

is not an eigenvector, since

and this vector is not a multiple of the original vector x.

Formal definition

In abstract mathematics, a more general definition is given:

Let V be any vector space

Vector space

A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...

, let x be a vector in that vector space, and let T be a linear transformation

Linear transformation

mapping V into V. Then x is an eigenvector of T with eigenvalue λ if the following equation holds:

This equation is called the eigenvalue equation. Note that Tx means T of x, the action of the transformation T on x, while λx means the product of the number λ times the vector x. Most, but not all authors also require x to be non-zero. The set of eigenvalues of T is sometimes called the spectrum of T.

Characteristic polynomial
The eigenvalues of A are precisely the solutions λ to the equation

Here det is the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...

of matrix formed by A - λI and I is the n×n identity matrix
Identity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...

. This equation is called the characteristic equation (or, less often, the secular equation) of A. For example, if A is the following matrix (a so-called diagonal matrix

Diagonal matrix

In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...

then the characteristic equation reads

.
The solutions to this equation are the eigenvalues λ_i = ai,i (i = 1, ..., n).

Proving the afore-mentioned relation of eigenvalues and solutions of the characteristic equation requires some linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...

, specifically the notion of linearly independent vectors
Linear independence
In linear algebra, a family of vectors is linearly independent if none of them can be written as a linear combination of finitely many other vectors in the collection. A family of vectors which is not linearly independent is called linearly dependent...

: briefly, the eigenvalue equation for a matrix A can be expressed as

which can be rearranged to

If there exists an inverse

then both sides can be left-multiplied by it, to obtain x = 0. Therefore, if λ is such that is invertible, λ cannot be an eigenvalue. It can be shown that the converse holds, too: if is not invertible, λ is an eigenvalue. A criterion from linear algebra states that a matrix (here: ) is non-invertible if and only if its determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...

is zero, thus leading to the characteristic equation.

The left-hand side of this equation can be seen (using Leibniz' rule for the determinant) to be a polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...

function in λ, whose coefficient
Coefficient
In mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...

s depend on the entries of A. This polynomial is called the characteristic polynomial

Characteristic polynomial

In linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....

. Its degree
Degree of a polynomial
The degree of a polynomial represents the highest degree of a polynominal's terms , should the polynomial be expressed in canonical form . The degree of an individual term is the sum of the exponents acting on the term's variables...

is n, that is to say, the highest power of λ occurring in this polynomial is λn. At least for small matrices, the solutions of the characteristic equation (hence, the eigenvalues of A) can be found directly. Moreover, it is important for theoretical purposes, such as the Cayley–Hamilton theorem
Cayley–Hamilton theorem
In linear algebra, the Cayley–Hamilton theorem states that every square matrix over a commutative ring satisfies its own characteristic equation....

. It also shows that any n×n matrix has at most n eigenvalues. However, the characteristic equation need not have n distinct solutions. In other words, there may be strictly less than n distinct eigenvalues. This happens for the matrix describing the shear mapping discussed below.

If the matrix has real entries, the coefficients of the characteristic polynomial are all real. However, the roots are not necessarily real; they may include complex numbers with a non-zero imaginary component. For example, a 2×2 matrix describing a 45° rotation will not leave any non-zero vector pointing in the same direction. However, there is at least one complex number

Complex number

A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...

λ solving the characteristic equation, even if the entries of the matrix A are complex numbers to begin with. (This existence of such a solution is known as the fundamental theorem of algebra
Fundamental theorem of algebra
The fundamental theorem of algebra states that every non-constant single-variable polynomial with complex coefficients has at least one complex root...

.) For a complex eigenvalue, the corresponding eigenvectors also have complex components.

Eigenspace
If x is an eigenvector of the matrix A with eigenvalue λ, then any scalar multiple αx is also an eigenvector of A with the same eigenvalue, since A(αx) = αAx = αλx = λ(αx). More generally, any non-zero linear combination of eigenvectors that share the same eigenvalue λ, will itself be an eigenvector with eigenvalue λ. Together with the zero vector, the eigenvectors of A with the same eigenvalue form a linear subspace

Linear subspace

The concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....

of the vector space called an eigenspace, E_λ. In case of dim(E_λ) = 1, it is called an eigenline and λ is called a scaling factor.
Diagonalizable matrices can be decomposed into a direct sum of eigenspaces, as per the eigendecomposition of a matrix

Eigendecomposition of a matrix

In the mathematical discipline of linear algebra, eigendecomposition or sometimes spectral decomposition is the factorization of a matrix into a canonical form, whereby the matrix is represented in terms of its eigenvalues and eigenvectors...

. If a matrix is not diagonalizable, then it is called defective

Defective matrix

In linear algebra, a defective matrix is a square matrix that does not have a complete basis of eigenvectors, and is therefore not diagonalizable. In particular, an n × n matrix is defective if and only if it does not have n linearly independent eigenvectors...

, and, while it cannot be decomposed into eigenspaces, it can be decomposed into the more general concept of generalized eigenspaces, as discussed here.

Algebraic and geometric multiplicities

Given an n×n matrix A and an eigenvalue λ_i of this matrix, there are two numbers measuring, roughly speaking, the number of eigenvectors belonging to λ_i. They are called multiplicities: the algebraic multiplicity of an eigenvalue is defined as the multiplicity of the corresponding root of the characteristic polynomial. The geometric multiplicity of an eigenvalue is defined as the dimension of the associated eigenspace, i.e. number of linearly independent eigenvectors with that eigenvalue. Both algebraic and geometric multiplicity are integers between (including) 1 and n. The algebraic multiplicity n_i and geometric multiplicity m_i may or may not be equal, but we always have m_i ≤ n_i. The simplest case is of course when m_i = n_i = 1. The total number of linearly independent eigenvectors, N_x, is given by summing the geometric multiplicities

Over a complex vector space, the sum of the algebraic multiplicities will equal the dimension of the vector space, but the sum of the geometric multiplicities may be smaller. In this case, it is possible that there may not be sufficient eigenvectors to span the entire space – more formally, there is no basis of eigenvectors (an ). A matrix is diagonalizable

Diagonalizable matrix

In linear algebra, a square matrix A is called diagonalizable if it is similar to a diagonal matrix, i.e., if there exists an invertible matrix P such that P −1AP is a diagonal matrix...

by a suitable choice of coordinates if and only if there is an eigenbasis; if a matrix is not diagonalizable, it is said to be defective

Defective matrix

. For defective matrices, the notion of eigenvector can be generalized to generalized eigenvector

Generalized eigenvector

In linear algebra, for a matrix A, there may not always exist a full set of linearly independent eigenvectors that form a complete basis – a matrix may not be diagonalizable. This happens when the algebraic multiplicity of at least one eigenvalue λ is greater than its geometric multiplicity...

s, and over an algebraically closed field a basis of generalized eigenvectors always exists, as follows from Jordan form.

The eigenvectors corresponding to different eigenvalues are linearly independent, meaning, in particular, that in an n-dimensional space the linear transformation A cannot have more than n eigenvalues (or eigenspaces). All defective matrices have fewer than n distinct eigenvalues, but not all matrices with fewer than n distinct eigenvalues are defective – for example, the identity matrix is diagonalizable (and indeed diagonal in any basis), but only has the eigenvalue 1.

Given an ordered choice of linearly independent eigenvectors, especially an eigenbasis, they can be indexed by eigenvalues, i.e. using a double index, with x_i,j being the j ^th eigenvector for the i ^th eigenvalue. The eigenvectors can also be indexed using the simpler notation of a single index x_k, with k = 1, 2, ... , N_x.

Worked example

These concepts are explained for the matrix

The characteristic equation of this matrix reads

Calculating the determinant

Determinant

In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...

, this yields the quadratic equation

Quadratic equation

In mathematics, a quadratic equation is a univariate polynomial equation of the second degree. A general quadratic equation can be written in the formax^2+bx+c=0,\,...

whose solutions (also called roots

Root system

In mathematics, a root system is a configuration of vectors in a Euclidean space satisfying certain geometrical properties. The concept is fundamental in the theory of Lie groups and Lie algebras...

) are

and

. The eigenvectors for the eigenvalue

are determined by using the eigenvalue equation, which in this case reads

The juxtaposition at the left hand side denotes matrix multiplication

Matrix multiplication

. Spelling this out, this equation comparing two vectors is tantamount to a system of the following two linear equation

Linear equation

A linear equation is an algebraic equation in which each term is either a constant or the product of a constant and a single variable....

Both equations reduce to the single linear equation

. That is to say, any vector of the form (x, y) with y = x is an eigenvector to the eigenvalue λ = 3. However, the vector (0, 0) is excluded. A similar calculation shows that the eigenvectors corresponding to the eigenvalue

are given by non-zero vectors (x, y) such that y = −x. For example, an eigenvector corresponding to

whereas an eigenvector corresponding to

. These vectors, placed as columns in a matrix, may be used to create a diagonalizable matrix

Diagonalizable matrix

In linear algebra, a square matrix A is called diagonalizable if it is similar to a diagonal matrix, i.e., if there exists an invertible matrix P such that P −1AP is a diagonal matrix...

Eigendecomposition

The spectral theorem

Spectral theorem

In mathematics, particularly linear algebra and functional analysis, the spectral theorem is any of a number of results about linear operators or about matrices. In broad terms the spectral theorem provides conditions under which an operator or a matrix can be diagonalized...

for matrices can be stated as follows. Let A be a square n × n matrix. Let q₁ ... q_k be an eigenvector basis, i.e. an indexed set of k linearly independent eigenvectors, where k is the dimension of the space spanned by the eigenvectors of A. If k = n, then A can be written

where Q is the square n × n matrix whose i-th column is the basis eigenvector q_i of A and Λ is the diagonal matrix

Diagonal matrix

In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...

whose diagonal elements are the corresponding eigenvalues, i.e. Λ_ii = λ_i.

Further properties

Let

be an n×n matrix with eigenvalues

. Then

Trace
Trace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...

of A.

Determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...

of A.

Eigenvalues of are

These first three results follow by putting the matrix in upper-triangular form, in which case the eigenvalues are on the diagonal and the trace and determinant are respectively the sum and product of the diagonal.

If , i.e., is Hermitian, every eigenvalue is real.

Every eigenvalue of a Unitary matrix has absolute value .

Examples in the plane

The following table presents some example transformations in the plane along with their 2×2 matrices, eigenvalues, and eigenvectors.

	horizontal shear	scaling Scaling (geometry) In Euclidean geometry, uniform scaling is a linear transformation that enlarges or shrinks objects by a scale factor that is the same in all directions. The result of uniform scaling is similar to the original...	unequal scaling	counterclockwise rotation by
illustration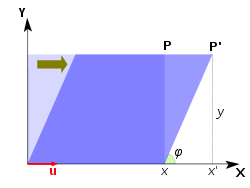
matrix
characteristic equation	λ² − 2λ+1 = (1 − λ)² = 0	λ² − 2λk + k² = (λ − k)² = 0	(λ − k₁)(λ − k₂) = 0	λ² − 2λ cos φ + 1 = 0
eigenvalues λ_i	λ₁=1	λ₁=k	λ₁ = k₁, λ₂ = k₂	λ_1,2 = cos φ ± i sin φ = e^{± iφ}
algebraic and geometric multiplicities	n₁ = 2, m₁ = 1	n₁ = 2, m₁ = 2	n₁ = m₁ = 1, n₂ = m₂ = 1	n₁ = m₁ = 1, n₂ = m₂ = 1
eigenvectors

Shear

Shear in the plane is a transformation where all points along a given line remain fixed while other points are shifted parallel to that line by a distance proportional to their perpendicular distance from the line. In the horizontal shear depicted above, a point P of the plane moves parallel to the x-axis to the place P' so that its coordinate y does not change while the x coordinate increments to become x' = x + k y, where k is called the shear factor. The shear angle φ is determined by k = cot φ.

Repeatedly applying the shear transformation changes the direction of any vector in the plane closer and closer to the direction of the eigenvector.

Uniform scaling and reflection

Multiplying every vector with a constant real number k is represented by the diagonal matrix

Diagonal matrix

In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...

whose entries on the diagonal are all equal to k. Mechanically, this corresponds to stretching a rubber sheet equally in all directions such as a small area of the surface of an inflating balloon. All vectors originating at origin

Origin (mathematics)

(i.e., the fixed point on the balloon surface) are stretched equally with the same scaling factor k while preserving its original direction. Thus, every non-zero vector is an eigenvector with eigenvalue k. Whether the transformation is stretching (elongation, extension, inflation), or shrinking (compression, deflation) depends on the scaling factor: if k > 1, it is stretching; if , it is shrinking. Negative values of k correspond to a reversal of direction, followed by a stretch or a shrink, depending on the absolute value of k.

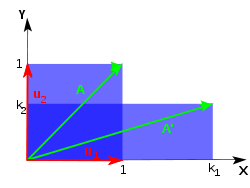
Unequal scaling

For a slightly more complicated example, consider a sheet that is stretched unequally in two perpendicular directions along the coordinate axes, or, similarly, stretched in one direction, and shrunk in the other direction. In this case, there are two different scaling factors: k₁ for the scaling in direction x, and k₂ for the scaling in direction y. If a given eigenvalue is greater than 1, the vectors are stretched in the direction of the corresponding eigenvector; if less than 1, they are shrunken in that direction. Negative eigenvalues correspond to reflections followed by a stretch or shrink. In general, matrices that are diagonalizable over the real numbers represent scalings and reflections: the eigenvalues represent the scaling factors (and appear as the diagonal terms), and the eigenvectors are the directions of the scalings.

The figure shows the case where

and

. The rubber sheet is stretched along the x axis and simultaneously shrunk along the y axis. After repeatedly applying this transformation of stretching/shrinking many times, almost any vector on the surface of the rubber sheet will be oriented closer and closer to the direction of the x axis (the direction of stretching). The exceptions are vectors along the y-axis, which will gradually shrink away to nothing.

Rotation

A rotation

Rotation (mathematics)

In geometry and linear algebra, a rotation is a transformation in a plane or in space that describes the motion of a rigid body around a fixed point. A rotation is different from a translation, which has no fixed points, and from a reflection, which "flips" the bodies it is transforming...

in a plane is a transformation that describes motion of a vector, plane, coordinates, etc., around a fixed point. Clearly, for rotations other than through 0° and 180°, every vector in the real plane will have its direction changed, and thus there cannot be any eigenvectors. But this is not necessarily true if we consider the same matrix over a complex vector space. The characteristic equation is a quadratic equation

Quadratic equation

In mathematics, a quadratic equation is a univariate polynomial equation of the second degree. A general quadratic equation can be written in the formax^2+bx+c=0,\,...

with discriminant

Discriminant

In algebra, the discriminant of a polynomial is an expression which gives information about the nature of the polynomial's roots. For example, the discriminant of the quadratic polynomialax^2+bx+c\,is\Delta = \,b^2-4ac....

D = 4 (cos² φ − 1) = − 4 sin² φ, which is a negative number whenever φ is not equal to a multiple of 180°. A rotation of 0°, 360°, … is just the identity transformation (a uniform scaling by +1), while a rotation of 180°, 540°, …, is a reflection (uniform scaling by -1). Otherwise, as expected, there are no real eigenvalues or eigenvectors for rotation in the plane. Instead, the eigenvalues are complex numbers in general. Although not diagonalizable over the reals, the rotation matrix is diagonalizable over the complex numbers, and again the eigenvalues appear on the diagonal. Thus rotation matrices acting on complex spaces can be thought of as scaling matrices, with complex scaling factors.

Calculation

The complexity of the problem for finding roots/eigenvalues of the characteristic polynomial increases rapidly with increasing the degree of the polynomial (the dimension of the vector space). There are exact solutions for dimensions below 5, but for dimensions greater than or equal to 5 there are generally no exact solutions and one has to resort to numerical methods to find them approximately. (In fact, since the roots of any polynomial can be expressed as eigenvalues of a companion matrix, the Abel–Ruffini theorem

Abel–Ruffini theorem

In algebra, the Abel–Ruffini theorem states that there is no general algebraic solution—that is, solution in radicals— to polynomial equations of degree five or higher.- Interpretation :...

implies that there is no general algebraic solution

Algebraic solution

An algebraic solution is a closed form expression that is the solution of an algebraic equation in terms of the coefficients, relying only on addition, subtraction, multiplication, division, and the extraction of roots ....

for eigenvalues of 5×5 or larger matrices: any general eigenvalue algorithm is necessarily approximate, although in practice one can obtain any desired accuracy.) Worse, any computational procedure that starts by computing the coefficients of the characteristic polynomial can be very inaccurate in the presence of round-off error

Round-off error

A round-off error, also called rounding error, is the difference between the calculated approximation of a number and its exact mathematical value. Numerical analysis specifically tries to estimate this error when using approximation equations and/or algorithms, especially when using finitely many...

, because the roots of a polynomial are an extremely sensitive function of the coefficients (see Wilkinson's polynomial). Efficient, accurate methods to compute eigenvalues and eigenvectors of arbitrary matrices were not known until the advent of the QR algorithm

QR algorithm

In numerical linear algebra, the QR algorithm is an eigenvalue algorithm: that is, a procedure to calculate the eigenvalues and eigenvectors of a matrix. The QR transformation was developed in the late 1950s by John G.F. Francis and by Vera N. Kublanovskaya , working independently...

in 1961.
Besides, combining Householder transformation

Householder transformation

In linear algebra, a Householder transformation is a linear transformation that describes a reflection about a plane or hyperplane containing the origin. Householder transformations are widely used in numerical linear algebra, to perform QR decompositions and in the first step of the QR algorithm...

with LU decomposition

LU decomposition

In linear algebra, LU decomposition is a matrix decomposition which writes a matrix as the product of a lower triangular matrix and an upper triangular matrix. The product sometimes includes a permutation matrix as well. This decomposition is used in numerical analysis to solve systems of linear...

can get better convergence than QR algorithm

QR algorithm

. For large Hermitian sparse matrices

Sparse matrix

In the subfield of numerical analysis, a sparse matrix is a matrix populated primarily with zeros . The term itself was coined by Harry M. Markowitz....

, the Lanczos algorithm

Lanczos algorithm

The Lanczos algorithm is an iterative algorithm invented by Cornelius Lanczos that is an adaptation of power methods to find eigenvalues and eigenvectors of a square matrix or the singular value decomposition of a rectangular matrix. It is particularly useful for finding decompositions of very...

is one example of an efficient iterative method

Iterative method

In computational mathematics, an iterative method is a mathematical procedure that generates a sequence of improving approximate solutions for a class of problems. A specific implementation of an iterative method, including the termination criteria, is an algorithm of the iterative method...

to compute eigenvalues and eigenvectors, among several other possibilities.

History

Eigenvalues are often introduced in the context of linear algebra

Linear algebra

or matrix theory. Historically, however, they arose in the study of quadratic form

Quadratic form

In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....

s and differential equation

Differential equation

A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...

s.

Euler

Leonhard Euler

Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...

studied the rotational motion of a rigid body

Rigid body

In physics, a rigid body is an idealization of a solid body of finite size in which deformation is neglected. In other words, the distance between any two given points of a rigid body remains constant in time regardless of external forces exerted on it...

and discovered the importance of the principal axes. Lagrange

Lagrange

La Grange literally means the barn in French. Lagrange may refer to:- People :* Charles Varlet de La Grange , French actor* Georges Lagrange , translator to and writer in Esperanto...

realized that the principal axes are the eigenvectors of the inertia matrix. In the early 19th century, Cauchy

Augustin Louis Cauchy

Baron Augustin-Louis Cauchy was a French mathematician who was an early pioneer of analysis. He started the project of formulating and proving the theorems of infinitesimal calculus in a rigorous manner, rejecting the heuristic principle of the generality of algebra exploited by earlier authors...

saw how their work could be used to classify the quadric surfaces, and generalized it to arbitrary dimensions. Cauchy also coined the term racine caractéristique (characteristic root) for what is now called eigenvalue; his term survives in characteristic equation.

Fourier

Joseph Fourier

Jean Baptiste Joseph Fourier was a French mathematician and physicist best known for initiating the investigation of Fourier series and their applications to problems of heat transfer and vibrations. The Fourier transform and Fourier's Law are also named in his honour...

used the work of Laplace and Lagrange to solve the heat equation

Heat equation

The heat equation is an important partial differential equation which describes the distribution of heat in a given region over time...

by separation of variables

Separation of variables

In mathematics, separation of variables is any of several methods for solving ordinary and partial differential equations, in which algebra allows one to rewrite an equation so that each of two variables occurs on a different side of the equation....

in his famous 1822 book Théorie analytique de la chaleur. Sturm developed Fourier's ideas further and brought them to the attention of Cauchy, who combined them with his own ideas and arrived at the fact that real symmetric matrices have real eigenvalues. This was extended by Hermite

Charles Hermite

Charles Hermite was a French mathematician who did research on number theory, quadratic forms, invariant theory, orthogonal polynomials, elliptic functions, and algebra....

in 1855 to what are now called Hermitian matrices. Around the same time, Brioschi

Francesco Brioschi

Francesco Brioschi was an Italian mathematician.Brioschi was born in Milan in 1824. From 1850 he taught analytical mechanics in the University of Pavia. After the Italian unification in 1861, he was elected depute in the Parliament of Italy and then appointed twice secretary of the Education...

proved that the eigenvalues of orthogonal matrices

Orthogonal matrix

In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....

lie on the unit circle

Unit circle

In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...

, and Clebsch

Alfred Clebsch

Rudolf Friedrich Alfred Clebsch was a German mathematician who made important contributions to algebraic geometry and invariant theory. He attended the University of Königsberg and was habilitated at Berlin. He subsequently taught in Berlin and Karlsruhe...

found the corresponding result for skew-symmetric matrices

Skew-symmetric matrix

In mathematics, and in particular linear algebra, a skew-symmetric matrix is a square matrix A whose transpose is also its negative; that is, it satisfies the equation If the entry in the and is aij, i.e...

. Finally, Weierstrass

Karl Weierstrass

Karl Theodor Wilhelm Weierstrass was a German mathematician who is often cited as the "father of modern analysis".- Biography :Weierstrass was born in Ostenfelde, part of Ennigerloh, Province of Westphalia....

clarified an important aspect in the stability theory

Stability theory

In mathematics, stability theory addresses the stability of solutions of differential equations and of trajectories of dynamical systems under small perturbations of initial conditions...

started by Laplace by realizing that defective matrices

Defective matrix

can cause instability.

In the meantime, Liouville

Joseph Liouville

- Life and work :Liouville graduated from the École Polytechnique in 1827. After some years as an assistant at various institutions including the Ecole Centrale Paris, he was appointed as professor at the École Polytechnique in 1838...

studied eigenvalue problems similar to those of Sturm; the discipline that grew out of their work is now called Sturm–Liouville theory. Schwarz

Hermann Schwarz

Karl Hermann Amandus Schwarz was a German mathematician, known for his work in complex analysis. He was born in Hermsdorf, Silesia and died in Berlin...

studied the first eigenvalue of Laplace's equation

Laplace's equation

In mathematics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace who first studied its properties. This is often written as:where ∆ = ∇² is the Laplace operator and \varphi is a scalar function...

on general domains towards the end of the 19th century, while Poincaré

Henri Poincaré

Jules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...

studied Poisson's equation

Poisson's equation

In mathematics, Poisson's equation is a partial differential equation of elliptic type with broad utility in electrostatics, mechanical engineering and theoretical physics...

a few years later.

At the start of the 20th century, Hilbert

David Hilbert

David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...

studied the eigenvalues of integral operators by viewing the operators as infinite matrices. He was the first to use the German

German language

word eigen to denote eigenvalues and eigenvectors in 1904, though he may have been following a related usage by Helmholtz. For some time, the standard term in English was "proper value", but the more distinctive term "eigenvalue" is standard today.

The first numerical algorithm for computing eigenvalues and eigenvectors appeared in 1929, when Von Mises

Richard Edler von Mises

Richard Edler von Mises was a scientist and mathematician who worked on solid mechanics, fluid mechanics, aerodynamics, aeronautics, statistics and probability theory. He held the position of Gordon-McKay Professor of Aerodynamics and Applied Mathematics at Harvard University...

published the power method. One of the most popular methods today, the QR algorithm

QR algorithm

, was proposed independently by John G.F. Francis

John G.F. Francis

John G.F. Francis is an English computer scientist, who in 1961 published the QR algorithm for computing the eigenvalues and eigenvectors of matrices, which has been named as one of the ten most important algorithms of the twentieth century. The algorithm was also proposed independently by Vera N...

and Vera Kublanovskaya

Vera Kublanovskaya

Vera Nikolaevna Kublanovskaya is a Russian mathematician noted for her work on developing computational methods for solving spectral problems of algebra. She proposed the QR algorithm for computing eigenvalues and eigenvectors in 1961, which has been named as one of the ten most important...

in 1961.

Left and right eigenvectors

The word eigenvector formally refers to the right eigenvector

. It is defined by the above eigenvalue equation

and is the most commonly used eigenvector. However, the left eigenvector

exists as well, and is defined by

Infinite-dimensional spaces and spectral theory

If the vector space is an infinite dimensional Banach space

Banach space

In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...

, the notion of eigenvalues can be generalized to the concept of spectrum

Spectrum (functional analysis)

In functional analysis, the concept of the spectrum of a bounded operator is a generalisation of the concept of eigenvalues for matrices. Specifically, a complex number λ is said to be in the spectrum of a bounded linear operator T if λI − T is not invertible, where I is the...

.
The spectrum is the set of scalars λ for which (T − λI)⁻¹ is not defined; that is, such that T − λI has no bounded

Bounded operator

In functional analysis, a branch of mathematics, a bounded linear operator is a linear transformation L between normed vector spaces X and Y for which the ratio of the norm of L to that of v is bounded by the same number, over all non-zero vectors v in X...

inverse.

Clearly if λ is an eigenvalue of T, λ is in the spectrum of T. In general, the converse is not true. There are operators on Hilbert

Hilbert space

The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...

or Banach space

Banach space

s that have no eigenvectors at all. This can be seen in the following example. The bilateral shift on the Hilbert space ℓ ²(Z) (that is, the space of all sequences of scalars … a₋₁, a₀, a₁, a₂, … such that

converges) has no eigenvalue but does have spectral values.

In infinite-dimensional spaces, the spectrum of a bounded operator

Bounded operator

is always nonempty. This is also true for an unbounded self adjoint operator. Via its spectral measures, the spectrum of any self adjoint operator, bounded or otherwise, can be decomposed into absolutely continuous, pure point, and singular parts. (See Decomposition of spectrum

Decomposition of spectrum (functional analysis)

In mathematics, especially functional analysis, the spectrum of an operator generalizes the notion of eigenvalues. Given an operator, it is sometimes useful to break up the spectrum into various parts...

.)

The hydrogen atom

Hydrogen atom

A hydrogen atom is an atom of the chemical element hydrogen. The electrically neutral atom contains a single positively-charged proton and a single negatively-charged electron bound to the nucleus by the Coulomb force...

is an example where both types of spectra appear. The eigenfunctions of the hydrogen atom Hamiltonian

Molecular Hamiltonian

In atomic, molecular, and optical physics as well as in quantum chemistry, molecular Hamiltonian is the name given to the Hamiltonian representing the energy of the electrons and nuclei in a molecule...

are called eigenstates and are grouped into two categories. The bound state

Bound state

In physics, a bound state describes a system where a particle is subject to a potential such that the particle has a tendency to remain localised in one or more regions of space...

s of the hydrogen atom correspond to the discrete part of the spectrum (they have a discrete set of eigenvalues that can be computed by Rydberg formula

Rydberg formula

The Rydberg formula is used in atomic physics to describe the wavelengths of spectral lines of many chemical elements. It was formulated by the Swedish physicist Johannes Rydberg, and presented on November 5, 1888.-History:...

) while the ionization

Ionization

Ionization is the process of converting an atom or molecule into an ion by adding or removing charged particles such as electrons or other ions. This is often confused with dissociation. A substance may dissociate without necessarily producing ions. As an example, the molecules of table sugar...

processes are described by the continuous part (the energy of the collision/ionization is not quantized).

Eigenfunctions

A common example of such maps on infinite dimensional spaces are the action of differential operator

Differential operator

In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...

s on function space

Function space

In mathematics, a function space is a set of functions of a given kind from a set X to a set Y. It is called a space because in many applications it is a topological space, a vector space, or both.-Examples:...

s. As an example, on the space of infinitely differentiable

Derivative

In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...

functions, the process of differentiation defines a linear operator since

where f(t) and g(t) are differentiable functions, and a and b are constants

Constant (mathematics)

In mathematics, a constant is a non-varying value, i.e. completely fixed or fixed in the context of use. The term usually occurs in opposition to variable In mathematics, a constant is a non-varying value, i.e. completely fixed or fixed in the context of use. The term usually occurs in opposition...

.

The eigenvalue equation for linear differential operators is then a set of one or more differential equation

Differential equation

A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...

s. The eigenvectors are commonly called eigenfunctions. The simplest case is the eigenvalue equation for differentiation of a real valued function by a single real variable. We seek a function (equivalent to an infinite-dimensional vector) that, when differentiated, yields a constant times the original function. In this case, the eigenvalue equation becomes the linear differential equation

Here λ is the eigenvalue associated with the function, f(x). This eigenvalue equation has a solution for any value of λ. If λ is zero, the solution is

where A is any constant; if λ is non-zero, the solution is the exponential function

Exponential function

In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...

If we expand our horizons to complex valued functions, the value of λ can be any complex number

Complex number

. The spectrum of d/dt is therefore the whole complex plane

Complex plane

In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...

. This is an example of a continuous spectrum

Continuous spectrum

The spectrum of a linear operator is commonly divided into three parts: point spectrum, continuous spectrum, and residual spectrum.If H is a topological vector space and A:H \to H is a linear map, the spectrum of A is the set of complex numbers \lambda such that A - \lambda I : H \to H is not...

Waves on a string

The displacement,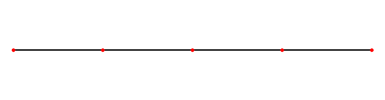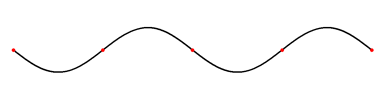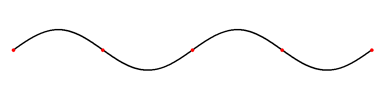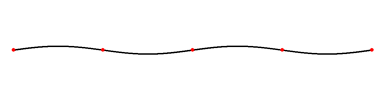

, of a stressed rope fixed at both ends, like the vibrating string

Vibrating string

A vibration in a string is a wave. Usually a vibrating string produces a sound whose frequency in most cases is constant. Therefore, since frequency characterizes the pitch, the sound produced is a constant note....

s of a string instrument

String instrument

A string instrument is a musical instrument that produces sound by means of vibrating strings. In the Hornbostel-Sachs scheme of musical instrument classification, used in organology, they are called chordophones...

, satisfies the wave equation

Wave equation

The wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...

which is a linear partial differential equation

Partial differential equation

In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...

, where c is the constant wave speed. The normal method of solving such an equation is separation of variables

Separation of variables

. If we assume that h can be written as the product of the form X(x)T(t), we can form a pair of ordinary differential equations:

and

Each of these is an eigenvalue equation (the unfamiliar form of the eigenvalue is chosen merely for convenience). For any values of the eigenvalues, the eigenfunctions are given by

and

If we impose boundary conditions (that the ends of the string are fixed with X(x) = 0 at x = 0 and x = L, for example) we can constrain the eigenvalues. For those boundary conditions

Boundary value problem

In mathematics, in the field of differential equations, a boundary value problem is a differential equation together with a set of additional restraints, called the boundary conditions...

, we find

, and so the phase angle

and

Thus, the constant

is constrained to take one of the values

, where n is any integer. Thus the clamped string supports a family of standing waves of the form

From the point of view of our musical instrument, the frequency

is the frequency of the nth harmonic

Harmonic

A harmonic of a wave is a component frequency of the signal that is an integer multiple of the fundamental frequency, i.e. if the fundamental frequency is f, the harmonics have frequencies 2f, 3f, 4f, . . . etc. The harmonics have the property that they are all periodic at the fundamental...

, which is called the (n-1)st overtone

Overtone

An overtone is any frequency higher than the fundamental frequency of a sound. The fundamental and the overtones together are called partials. Harmonics are partials whose frequencies are whole number multiples of the fundamental These overlapping terms are variously used when discussing the...

Associative algebras and representation theory

More algebraically, rather than generalizing the vector space to an infinite dimensional space, one can generalize the algebraic object that is acting on the space, replacing a single operator acting on a vector space with an algebra representation – an associative algebra

Associative algebra

In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...

acting on a module. The study of such actions is the field of representation theory

Representation theory

Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...

. To understand these representations, one breaks them into indecomposable representations, and, if possible, into irreducible representations; these correspond respectively to generalized eigenspaces and eigenspaces, or rather the indecomposable and irreducible components of these. While a single operator on a vector space can be understood in terms of eigenvectors – 1-dimensional invariant subspaces – in general in representation theory the building blocks (the irreducible representations) are higher-dimensional.

A closer analog of eigenvalues is given by the notion of a weight
Weight (representation theory)
In the mathematical field of representation theory, a weight of an algebra A over a field F is an algebra homomorphism from A to F – a linear functional – or equivalently, a one dimensional representation of A over F. It is the algebra analogue of a multiplicative character of a group...

, with the analogs of eigenvectors and eigenspaces being weight vectors and weight spaces. For an associative algebra A over a field F, the analog of an eigenvalue is a one-dimensional representation

(a map of algebras; a linear functional

Linear functional

In linear algebra, a linear functional or linear form is a linear map from a vector space to its field of scalars. In Rn, if vectors are represented as column vectors, then linear functionals are represented as row vectors, and their action on vectors is given by the dot product, or the...

that is also multiplicative), called the weight, rather than a single scalar. A map of algebras is used because if a vector is an eigenvector for two elements of an algebra, then it is also an eigenvector for any linear combination of these, and the eigenvalue is the corresponding linear combination of the eigenvalues, and likewise for multiplication. This is related to the classical eigenvalue as follows: a single operator T corresponds to the algebra F[T] (the polynomials in T), and a map of algebras

is determined by its value on the generator T; this value is the eigenvalue. A vector v on which the algebra acts by this weight (i.e., by scalar multiplication, with the scalar determined by the weight) is called a weight vector, and other concepts generalize similarly. The generalization of a diagonalizable matrix (having an eigenbasis) is a weight module.

Because a weight is a map to a field, which is commutative, the map factors through the abelianization of the algebra A – equivalently, it vanishes on the derived algebra – in terms of matrices, if v is a common eigenvector of operators T and U, then

(because in both cases it is just multiplication by scalars), so common eigenvectors of an algebra must be in the set on which the algebra acts commutatively (which is annihilated by the derived algebra). Thus of central interest are the free commutative algebras, namely the polynomial algebras. In this particularly simple and important case of the polynomial algebra

in a set of commuting matrices, a weight vector of this algebra is a simultaneous eigenvector of the matrices, while a weight of this algebra is simply a k-tuple of scalars

corresponding to the eigenvalue of each matrix, and hence geometrically to a point in k-space. These weights – in particularly their geometry – are of central importance in understanding the representation theory of Lie algebras, specifically the finite-dimensional representations of semisimple Lie algebras.

As an application of this geometry, given an algebra that is a quotient of a polynomial algebra on k generators, it corresponds geometrically to an algebraic variety

Algebraic variety

In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...

in k-dimensional space, and the weight must fall on the variety – i.e., it satisfies defining equations for the variety. This generalizes the fact that eigenvalues satisfy the characteristic polynomial of a matrix in one variable.

Schrödinger equation

An example of an eigenvalue equation where the transformation T is represented in terms of a differential operator is the time-independent Schrödinger equation

Schrödinger equation

The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....

in quantum mechanics

Quantum mechanics

where H, the Hamiltonian

Hamiltonian (quantum mechanics)

In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...

, is a second-order differential operator

Differential operator

and

, the wavefunction

Wavefunction

Not to be confused with the related concept of the Wave equationA wave function or wavefunction is a probability amplitude in quantum mechanics describing the quantum state of a particle and how it behaves. Typically, its values are complex numbers and, for a single particle, it is a function of...

, is one of its eigenfunctions corresponding to the eigenvalue E, interpreted as its energy

Energy

In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...

.

However, in the case where one is interested only in the bound state

Bound state

In physics, a bound state describes a system where a particle is subject to a potential such that the particle has a tendency to remain localised in one or more regions of space...

solutions of the Schrödinger equation, one looks for

within the space of square integrable

Square-integrable function

In mathematics, a quadratically integrable function, also called a square-integrable function, is a real- or complex-valued measurable function for which the integral of the square of the absolute value is finite...

functions. Since this space is a Hilbert space

Hilbert space

with a well-defined scalar product, one can introduce a basis set

Basis (linear algebra)

In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...

in which

and H can be represented as a one-dimensional array and a matrix respectively. This allows one to represent the Schrödinger equation in a matrix form.

Bra-ket notation

Bra-ket notation

Bra-ket notation is a standard notation for describing quantum states in the theory of quantum mechanics composed of angle brackets and vertical bars. It can also be used to denote abstract vectors and linear functionals in mathematics...

is often used in this context. A vector, which represents a state of the system, in the Hilbert space of square integrable functions is represented by

. In this notation, the Schrödinger equation is:

where

is an eigenstate of H. It is a self adjoint operator, the infinite dimensional analog of Hermitian matrices (see Observable
Observable
In physics, particularly in quantum physics, a system observable is a property of the system state that can be determined by some sequence of physical operations. For example, these operations might involve submitting the system to various electromagnetic fields and eventually reading a value off...

). As in the matrix case, in the equation above

is understood to be the vector obtained by application of the transformation H to

Molecular orbitals

In quantum mechanics

Quantum mechanics

, and in particular in atomic

Atomic physics

Atomic physics is the field of physics that studies atoms as an isolated system of electrons and an atomic nucleus. It is primarily concerned with the arrangement of electrons around the nucleus and...

and molecular physics

Molecular physics

Molecular physics is the study of the physical properties of molecules, the chemical bonds between atoms as well as the molecular dynamics. Its most important experimental techniques are the various types of spectroscopy...

, within the Hartree–Fock theory, the atomic

Atomic orbital

An atomic orbital is a mathematical function that describes the wave-like behavior of either one electron or a pair of electrons in an atom. This function can be used to calculate the probability of finding any electron of an atom in any specific region around the atom's nucleus...

and molecular orbital

Molecular orbital

In chemistry, a molecular orbital is a mathematical function describing the wave-like behavior of an electron in a molecule. This function can be used to calculate chemical and physical properties such as the probability of finding an electron in any specific region. The term "orbital" was first...

s can be defined by the eigenvectors of the Fock operator. The corresponding eigenvalues are interpreted as ionization potential

Ionization potential

The ionization energy of a chemical species, i.e. an atom or molecule, is the energy required to remove an electron from the species to a practically infinite distance. Large atoms or molecules have a low ionization energy, while small molecules tend to have higher ionization energies.The property...

s via Koopmans' theorem

Koopmans' theorem

Koopmans' theorem states that in closed-shell Hartree-Fock theory, the first ionization energy of a molecular system is equal to the negative of the orbital energy of the highest occupied molecular orbital...

. In this case, the term eigenvector is used in a somewhat more general meaning, since the Fock operator is explicitly dependent on the orbitals and their eigenvalues. If one wants to underline this aspect one speaks of nonlinear eigenvalue problem. Such equations are usually solved by an iteration

Iteration

Iteration means the act of repeating a process usually with the aim of approaching a desired goal or target or result. Each repetition of the process is also called an "iteration," and the results of one iteration are used as the starting point for the next iteration.-Mathematics:Iteration in...

procedure, called in this case self-consistent field method. In quantum chemistry

Quantum chemistry

Quantum chemistry is a branch of chemistry whose primary focus is the application of quantum mechanics in physical models and experiments of chemical systems...

, one often represents the Hartree–Fock equation in a non-orthogonal basis set

Basis set (chemistry)

A basis set in chemistry is a set of functions used to create the molecular orbitals, which are expanded as a linear combination of such functions with the weights or coefficients to be determined. Usually these functions are atomic orbitals, in that they are centered on atoms. Otherwise, the...

. This particular representation is a generalized eigenvalue problem called Roothaan equations

Roothaan equations

The Roothaan equations are a representation of the Hartree-Fock equation in a non orthonormal basis set which can be of Gaussian-type or Slater-type. It applies to closed-shell molecules or atoms where all molecular orbitals or atomic orbitals, respectively, are doubly occupied. This is generally...

Geology and glaciology

In geology

Geology

Geology is the science comprising the study of solid Earth, the rocks of which it is composed, and the processes by which it evolves. Geology gives insight into the history of the Earth, as it provides the primary evidence for plate tectonics, the evolutionary history of life, and past climates...

, especially in the study of glacial till, eigenvectors and eigenvalues are used as a method by which a mass of information of a clast fabric's constituents' orientation and dip can be summarized in a 3-D space by six numbers. In the field, a geologist may collect such data for hundreds or thousands of clasts in a soil sample, which can only be compared graphically such as in a Tri-Plot (Sneed and Folk) diagram, or as a Stereonet on a Wulff Net. The output for the orientation tensor is in the three orthogonal (perpendicular) axes of space. Eigenvectors output from programs such as Stereo32 are in the order E₁ ≥ E₂ ≥ E₃, with E₁ being the primary orientation of clast orientation/dip, E₂ being the secondary and E₃ being the tertiary, in terms of strength. The clast orientation is defined as the eigenvector, on a compass rose of 360°. Dip is measured as the eigenvalue, the modulus of the tensor: this is valued from 0° (no dip) to 90° (vertical). The relative values of E₁, E₂, and E₃ are dictated by the nature of the sediment's fabric. If E₁ = E₂ = E₃, the fabric is said to be isotropic. If E₁ = E₂ > E₃ the fabric is planar. If E₁ > E₂ > E₃ the fabric is linear. See 'A Practical Guide to the Study of Glacial Sediments' by Benn & Evans, 2004.

Principal components analysis

The eigendecomposition of a symmetric positive semidefinite (PSD) matrix yields an orthogonal basis

Orthogonal basis

In mathematics, particularly linear algebra, an orthogonal basis for an inner product space is a basis for whose vectors are mutually orthogonal...

of eigenvectors, each of which has a nonnegative eigenvalue. The orthogonal decomposition of a PSD matrix is used in multivariate analysis

Multivariate statistics

Multivariate statistics is a form of statistics encompassing the simultaneous observation and analysis of more than one statistical variable. The application of multivariate statistics is multivariate analysis...

, where the sample covariance matrices

Covariance matrix

In probability theory and statistics, a covariance matrix is a matrix whose element in the i, j position is the covariance between the i th and j th elements of a random vector...

are PSD. This orthogonal decomposition is called principal components analysis

Principal components analysis

Principal component analysis is a mathematical procedure that uses an orthogonal transformation to convert a set of observations of possibly correlated variables into a set of values of uncorrelated variables called principal components. The number of principal components is less than or equal to...

(PCA) in statistics. PCA studies linear relations among variables. PCA is performed on the covariance matrix

Covariance matrix

In probability theory and statistics, a covariance matrix is a matrix whose element in the i, j position is the covariance between the i th and j th elements of a random vector...

or the correlation matrix (in which each variable is scaled to have its sample variance equal to one). For the covariance or correlation matrix, the eigenvectors correspond to principal components

Principal components analysis

and the eigenvalues to the variance explained by the principal components. Principal component analysis of the correlation matrix provides an orthonormal eigen-basis

Orthogonal basis

In mathematics, particularly linear algebra, an orthogonal basis for an inner product space is a basis for whose vectors are mutually orthogonal...

for the space of the observed data: In this basis, the largest eigenvalues correspond to the principal-components that are associated with most of the covariability among a number of observed data.

Principal component analysis is used to study large

Data mining

Data mining , a relatively young and interdisciplinary field of computer science is the process of discovering new patterns from large data sets involving methods at the intersection of artificial intelligence, machine learning, statistics and database systems...

data set

Data set

A data set is a collection of data, usually presented in tabular form. Each column represents a particular variable. Each row corresponds to a given member of the data set in question. Its values for each of the variables, such as height and weight of an object or values of random numbers. Each...

s, such as those encountered in data mining

Data mining

, chemical research

Chemometrics

Chemometrics is the science of extracting information from chemical systems by data-driven means. It is a highly interfacial discipline, using methods frequently employed in core data-analytic disciplines such as multivariate statistics, applied mathematics, and computer science, in order to...

, psychology

Psychometrics

Psychometrics is the field of study concerned with the theory and technique of psychological measurement, which includes the measurement of knowledge, abilities, attitudes, personality traits, and educational measurement...

, and in marketing

Marketing

Marketing is the process used to determine what products or services may be of interest to customers, and the strategy to use in sales, communications and business development. It generates the strategy that underlies sales techniques, business communication, and business developments...

. PCA is popular especially in psychology, in the field of psychometrics

Psychometrics

. In Q-methodology

Q methodology

Q Methodology is a research method used in psychology and other social sciences to study people's "subjectivity" -- that is, their viewpoint. Q was developed by psychologist William Stephenson...

, the eigenvalues of the correlation matrix determine the Q-methodologist's judgment of practical significance (which differs from the statistical significance

Statistical significance

In statistics, a result is called statistically significant if it is unlikely to have occurred by chance. The phrase test of significance was coined by Ronald Fisher....

of hypothesis testing): The factors with eigenvalues greater than 1.00 are considered practically significant, that is, as explaining an important amount of the variability in the data, while eigenvalues less than 1.00 are considered practically insignificant, as explaining only a negligible portion of the data variability. More generally, principal component analysis can be used as a method of factor analysis

Factor analysis

Factor analysis is a statistical method used to describe variability among observed, correlated variables in terms of a potentially lower number of unobserved, uncorrelated variables called factors. In other words, it is possible, for example, that variations in three or four observed variables...

in structural equation modeling.

Vibration analysis

Eigenvalue problems occur naturally in the vibration analysis of mechanical structures with many degrees of freedom. The eigenvalues are used to determine the natural frequencies (or eigenfrequencies) of vibration, and the eigenvectors determine the shapes of these vibrational modes. In particular, undamped vibration is governed by

that is, acceleration is proportional to position (i.e., we expect x to be sinusoidal in time). In n dimensions, m becomes a mass matrix

Mass matrix

In computational mechanics, a mass matrix is a generalization of the concept of mass to generalized coordinates. For example, consider a two-body particle system in one dimension...

and k a stiffness matrix. Admissible solutions are then a linear combination of solutions to the generalized eigenvalue problem

where

is the eigenvalue and

is the angular frequency

Angular frequency

In physics, angular frequency ω is a scalar measure of rotation rate. Angular frequency is the magnitude of the vector quantity angular velocity...

. Note that the principal vibration modes are different from the principal compliance modes, which are the eigenvectors of k alone. Furthermore, damped vibration, governed by

leads to what is called a so-called quadratic eigenvalue problem,

.
This can be reduced to a generalized eigenvalue problem by clever algebra at the cost of solving a larger system.

The orthogonality properties of the eigenvectors allows decoupling of the differential equations so that the system can be represented as linear summation of the eigenvectors. The eigenvalue problem of complex structures is often solved using finite element analysis, but neatly generalize the solution to scalar-valued vibration problems.

Eigenfaces

In image processing

Image processing

In electrical engineering and computer science, image processing is any form of signal processing for which the input is an image, such as a photograph or video frame; the output of image processing may be either an image or, a set of characteristics or parameters related to the image...

, processed images of face

Face

The face is a central sense organ complex, for those animals that have one, normally on the ventral surface of the head, and can, depending on the definition in the human case, include the hair, forehead, eyebrow, eyelashes, eyes, nose, ears, cheeks, mouth, lips, philtrum, temple, teeth, skin, and...

s can be seen as vectors whose components are the brightness

Brightness

Brightness is an attribute of visual perception in which a source appears to be radiating or reflecting light. In other words, brightness is the perception elicited by the luminance of a visual target...

es of each pixel

Pixel

In digital imaging, a pixel, or pel, is a single point in a raster image, or the smallest addressable screen element in a display device; it is the smallest unit of picture that can be represented or controlled....

. The dimension of this vector space is the number of pixels. The eigenvectors of the covariance matrix

Covariance matrix

In probability theory and statistics, a covariance matrix is a matrix whose element in the i, j position is the covariance between the i th and j th elements of a random vector...

associated with a large set of normalized pictures of faces are called eigenface
Eigenface
Eigenfaces are a set of eigenvectors used in the computer vision problem of human face recognition. The approach of using eigenfaces for recognition was developed by Sirovich and Kirby and used by Matthew Turk and Alex Pentland in face classification. It is considered the first successful example...

s; this is an example of principal components analysis

Principal components analysis

. They are very useful for expressing any face image as a linear combination

Linear combination

In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...

of some of them. In the facial recognition

Facial recognition system

A facial recognition system is a computer application for automatically identifying or verifying a person from a digital image or a video frame from a video source...

branch of biometrics

Biometrics

Biometrics As Jain & Ross point out, "the term biometric authentication is perhaps more appropriate than biometrics since the latter has been historically used in the field of statistics to refer to the analysis of biological data [36]" . consists of methods...

, eigenfaces provide a means of applying data compression

Data compression

In computer science and information theory, data compression, source coding or bit-rate reduction is the process of encoding information using fewer bits than the original representation would use....

to faces for identification purposes. Research related to eigen vision systems determining hand gestures has also been made.

Similar to this concept, eigenvoices represent the general direction of variability in human pronunciations of a particular utterance, such as a word in a language. Based on a linear combination of such eigenvoices, a new voice pronunciation of the word can be constructed. These concepts have been found useful in automatic speech recognition systems, for speaker adaptation.

Tensor of inertia

In mechanics

Mechanics

Mechanics is the branch of physics concerned with the behavior of physical bodies when subjected to forces or displacements, and the subsequent effects of the bodies on their environment....

, the eigenvectors of the inertia tensor define the principal axes of a rigid body

Rigid body

. The tensor

Tensor

Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...

of inertia

Inertia

Inertia is the resistance of any physical object to a change in its state of motion or rest, or the tendency of an object to resist any change in its motion. It is proportional to an object's mass. The principle of inertia is one of the fundamental principles of classical physics which are used to...

is a key quantity required to determine the rotation of a rigid body around its center of mass

Center of mass

In physics, the center of mass or barycenter of a system is the average location of all of its mass. In the case of a rigid body, the position of the center of mass is fixed in relation to the body...

Stress tensor

In solid mechanics

Solid mechanics

Solid mechanics is the branch of mechanics, physics, and mathematics that concerns the behavior of solid matter under external actions . It is part of a broader study known as continuum mechanics. One of the most common practical applications of solid mechanics is the Euler-Bernoulli beam equation...

, the stress tensor

Stress tensor

Stress tensor may refer to:* Stress , in classical physics* Stress-energy tensor, in relativistic theories* Maxwell stress tensor, in electromagnetism...

is symmetric and so can be decomposed into a diagonal

Diagonal

A diagonal is a line joining two nonconsecutive vertices of a polygon or polyhedron. Informally, any sloping line is called diagonal. The word "diagonal" derives from the Greek διαγώνιος , from dia- and gonia ; it was used by both Strabo and Euclid to refer to a line connecting two vertices of a...

tensor with the eigenvalues on the diagonal and eigenvectors as a basis. Because it is diagonal, in this orientation, the stress tensor has no shear

Shear (mathematics)

In mathematics, shear mapping or transvection is a particular kind of linear mapping. Linear mapping is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication...

components; the components it does have are the principal components.

Eigenvalues of a graph

In spectral graph theory

Spectral graph theory

In mathematics, spectral graph theory is the study of properties of a graph in relationship to the characteristic polynomial, eigenvalues, and eigenvectors of matrices associated to the graph, such as its adjacency matrix or Laplacian matrix....

, an eigenvalue of a graph

Graph theory

In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...

is defined as an eigenvalue of the graph's adjacency matrix

Adjacency matrix

In mathematics and computer science, an adjacency matrix is a means of representing which vertices of a graph are adjacent to which other vertices...

A, or (increasingly) of the graph's
Laplacian matrix

Laplacian matrix

In the mathematical field of graph theory the Laplacian matrix, sometimes called admittance matrix or Kirchhoff matrix, is a matrix representation of a graph. Together with Kirchhoff's theorem it can be used to calculate the number of spanning trees for a given graph. The Laplacian matrix can be...

(see also Discrete Laplace operator

Discrete Laplace operator

In mathematics, the discrete Laplace operator is an analog of the continuous Laplace operator, defined so that it has meaning on a graph or a discrete grid...

), which is either T−A (sometimes called the Combinatorial Laplacian) or I−T^−1/2AT^−1/2 (sometimes called the Normalized Laplacian), where T is a diagonal matrix with T_v,v equal to the degree of vertex v, and in T^−1/2, the v^th diagonal entry is deg(v)^−1/2. The k^th principal eigenvector of a graph is defined as either the eigenvector corresponding to the k^th largest or k^th smallest eigenvalue of the Laplacian. The first principal eigenvector of the graph is also referred to merely as the principal eigenvector.

The principal eigenvector is used to measure the centrality of its vertices. An example is Google

Google

Google Inc. is an American multinational public corporation invested in Internet search, cloud computing, and advertising technologies. Google hosts and develops a number of Internet-based services and products, and generates profit primarily from advertising through its AdWords program...

's PageRank

PageRank

PageRank is a link analysis algorithm, named after Larry Page and used by the Google Internet search engine, that assigns a numerical weighting to each element of a hyperlinked set of documents, such as the World Wide Web, with the purpose of "measuring" its relative importance within the set...

algorithm. The principal eigenvector of a modified adjacency matrix

Adjacency matrix

In mathematics and computer science, an adjacency matrix is a means of representing which vertices of a graph are adjacent to which other vertices...

of the World Wide Web graph gives the page ranks as its components. This vector corresponds to the stationary distribution

Stationary distribution

Stationary distribution may refer to:* The limiting distribution in a Markov chain* The marginal distribution of a stationary process or stationary time series* The set of joint probability distributions of a stationary process or stationary time series...

of the Markov chain

Markov chain

A Markov chain, named after Andrey Markov, is a mathematical system that undergoes transitions from one state to another, between a finite or countable number of possible states. It is a random process characterized as memoryless: the next state depends only on the current state and not on the...

represented by the row-normalized adjacency matrix; however, the adjacency matrix must first be modified to ensure a stationary distribution exists. The second smallest eigenvector can be used to partition the graph into clusters, via spectral clustering. Other methods are also available for clustering.

Basic reproduction number

See Basic reproduction number
Basic reproduction number
In epidemiology, the basic reproduction number of an infection is the mean number of secondary cases caused by an individual infected soon after disease introduction into a population with no pre-existing immunity to the disease in the absence of interventions to control...

The basic reproduction number (

) is a fundamental number in the study of how infectious diseases spread. If one infectious person is put into a population of completely susceptible people, then

is the average number of people that one infectious person will infect. The generation time of an infection is the time,

, from one person become infected to the next person becoming infected. In a heterogenous population, the next generation matrix defines how many people in the population will become infected after time

has passed.

is then the largest eigenvalue of the next generation matrix. This result is due to Heesterbeek, at the University of Utrecht.

External links

What are Eigen Values? — non-technical introduction from PhysLink.com's "Ask the Experts"
Eigen Values and Eigen Vectors Numerical Examples – Tutorial and Interactive Program from Revoledu.
Introduction to Eigen Vectors and Eigen Values – lecture from Khan Academy

Theory

Eigenvector — Wolfram MathWorld
MathWorld
MathWorld is an online mathematics reference work, created and largely written by Eric W. Weisstein. It is sponsored by and licensed to Wolfram Research, Inc. and was partially funded by the National Science Foundation's National Science Digital Library grant to the University of Illinois at...
Eigen Vector Examination working applet
Same Eigen Vector Examination as above in a Flash demo with sound
Computation of Eigenvalues
Numerical solution of eigenvalue problems Edited by Zhaojun Bai, James Demmel
James Demmel
James Weldon Demmel is an American mathematician and computer scientist, the Dr. Richard Carl Dehmel Distinguished Professor of Mathematics and Computer Science at the University of California, Berkeley....

, Jack Dongarra, Axel Ruhe, and Henk van der Vorst
Henk van der Vorst
Hendrik "Henk" Albertus van der Vorst is a Dutch mathematician and Emeritus Professor of Numerical Analysis at Utrecht University...
Eigenvalues and Eigenvectors on the Ask Dr. Math forums: http://mathforum.org/library/drmath/view/55483.html, http://mathforum.org/library/drmath/view/51989.html

Online calculators

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.

Prerequisites and motivation

Example

Formal definition

Characteristic polynomial

Eigenspace

Algebraic and geometric multiplicities

Worked example

Eigendecomposition

Further properties

Examples in the plane

Shear

Uniform scaling and reflection

Unequal scaling

Rotation

Calculation

History

Left and right eigenvectors

Infinite-dimensional spaces and spectral theory

Eigenfunctions

Waves on a string

Associative algebras and representation theory

Schrödinger equation

Molecular orbitals

Geology and glaciology

Principal components analysis

Vibration analysis

Eigenfaces

Tensor of inertia

Stress tensor

Eigenvalues of a graph

Basic reproduction number

See also

External links