
Infimum
Encyclopedia

Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the infimum (plural infima) of a subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
S of some partially ordered set
Partially ordered set
In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
T is the greatest element
Greatest element
In mathematics, especially in order theory, the greatest element of a subset S of a partially ordered set is an element of S which is greater than or equal to any other element of S. The term least element is defined dually...
of T that is less than or equal to all elements of S. Consequently the term greatest lower bound (also abbreviated as glb or GLB) is also commonly used. Infima of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s are a common special case that is especially important in analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
. However, the general definition remains valid in the more abstract setting of order theory
Order theory
Order theory is a branch of mathematics which investigates our intuitive notion of order using binary relations. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article introduces the field and gives some basic definitions...
where arbitrary partially ordered set
Partially ordered set
In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
s are considered.
If the infimum exists, it is unique. If S contains a least element
Greatest element
In mathematics, especially in order theory, the greatest element of a subset S of a partially ordered set is an element of S which is greater than or equal to any other element of S. The term least element is defined dually...
, then that element is the infimum; otherwise, the infimum does not belong to S (or does not exist). For instance, the positive real numbers do not have a least element, and their infimum is 0, which is not a positive real number.
The infimum is in a precise sense dual
Duality (order theory)
In the mathematical area of order theory, every partially ordered set P gives rise to a dual partially ordered set which is often denoted by Pop or Pd. This dual order Pop is defined to be the set with the inverse order, i.e. x ≤ y holds in Pop if and only if y ≤ x holds in P...
to the concept of a supremum
Supremum
In mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
.
Infima of real numbers
In analysisMathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
the infimum or greatest lower bound of a subset S of real numbers is denoted by inf(S) and is defined to be the biggest real number that is smaller than or equal to every number in S. If no such number exists (because S is not bounded below), then we define inf(S) = −∞. If S is empty
Empty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
, we define inf(S) = ∞ (see extended real number line
Extended real number line
In mathematics, the affinely extended real number system is obtained from the real number system R by adding two elements: +∞ and −∞ . The projective extended real number system adds a single object, ∞ and makes no distinction between "positive" or "negative" infinity...
).
An important property of the real numbers is that every set of real numbers has an infimum (any bounded nonempty subset of the real numbers has an infimum in the non-extended real numbers).
Examples:
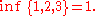
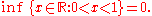
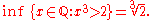
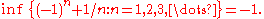
If a set has a smallest element, as in the first example, then the smallest element is the infimum for the set. (If the infimum is contained in the set, then it is also known as the minimum). As the last three examples show, the infimum of a set does not have to belong to the set.
The notions of infimum and supremum
Supremum
In mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
are dual in the sense that
 ,
,where

See also: limit inferior.
Infima in partially ordered sets
The definition of infima easily generalizes to subsets of arbitrary partially ordered setPartially ordered set
In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
s and as such plays a vital role in order theory
Order theory
Order theory is a branch of mathematics which investigates our intuitive notion of order using binary relations. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article introduces the field and gives some basic definitions...
. In this context, especially in lattice theory
Lattice (order)
In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
, greatest lower bounds are also called meets.
Formally, the infimum of a subset S of a partially ordered set (P, ≤) is an element a of P such that
- a ≤ x for all x in S, (a is a lower bound) and
- for all y in P, if for all x in S, y ≤ x, then y ≤ a (a larger than any other lower bound).
Any element with these properties is necessarily unique, but in general no such element needs to exist. Consequently, orders for which certain infima are known to exist become especially interesting. More information on the various classes of partially ordered sets that arise from such considerations are found in the article on completeness properties
Completeness (order theory)
In the mathematical area of order theory, completeness properties assert the existence of certain infima or suprema of a given partially ordered set . A special use of the term refers to complete partial orders or complete lattices...
.
The dual
Duality (order theory)
In the mathematical area of order theory, every partially ordered set P gives rise to a dual partially ordered set which is often denoted by Pop or Pd. This dual order Pop is defined to be the set with the inverse order, i.e. x ≤ y holds in Pop if and only if y ≤ x holds in P...
concept of infimum is given by the notion of a supremum
Supremum
In mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
or least upper bound. By the duality principle of order theory, every statement about suprema is thus readily transformed into a statement about infima. For this reason, all further results, details, and examples can be taken from the article on suprema
Supremum
In mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
.
See also
- SupremumSupremumIn mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
- Essential suprema and infima
- Limit superior and limit inferiorLimit superior and limit inferiorIn mathematics, the limit inferior and limit superior of a sequence can be thought of as limiting bounds on the sequence...
(infimum limit)

