
Poincaré metric
Encyclopedia
In mathematics
, the Poincaré metric, named after Henri Poincaré
, is the metric tensor
describing a two-dimensional surface of constant negative curvature
. It is the natural metric commonly used in a variety of calculations in hyperbolic geometry
or Riemann surface
s.
There are three equivalent representations commonly used in two-dimensional hyperbolic geometry
. One is the Poincaré half-plane model
, defining a model of hyperbolic space on the upper half-plane. The Poincaré disk model
defines a model for hyperbolic space on the unit disk. The disk and the upper half plane are related by a conformal map
, and isometries
are given by Mobius transformations. A third representation is on the punctured disk, where relations for q-analog
ues are sometimes expressed. These various forms are reviewed below.

where λ is a real, positive function of z and . The length of a curve γ in the complex plane is thus given by
. The length of a curve γ in the complex plane is thus given by
The area of a subset of the complex plane is given by
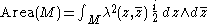
where is the exterior product used to construct the volume form
is the exterior product used to construct the volume form
. The determinant of the metric is equal to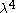 , so the square root of the determinant is
, so the square root of the determinant is  . The Euclidean volume form on the plane is
. The Euclidean volume form on the plane is  and so one has
and so one has

A function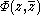 is said to be the potential of the metric if
is said to be the potential of the metric if
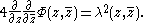
The Laplace–Beltrami operator is given by

The Gaussian curvature
of the metric is given by

This curvature is one-half of the Ricci scalar curvature.
Isometries preserve angles and arc-lengths. On Riemann surfaces, isometries are identical to changes of coordinate: that is, both the Laplace–Beltrami operator and the curvature are invariant under isometries. Thus, for example, let S be a Riemann surface with metric and T be a Riemann surface with metric
and T be a Riemann surface with metric  . Then a map
. Then a map

with is an isometry if and only if it is conformal and if
is an isometry if and only if it is conformal and if
 .
.
Here, the requirement that the map is conformal is nothing more than the statement

that is,

is given on the upper half-plane H as

where we write
This metric tensor is invariant under the action of SL(2,R). That is, if we write

for then we can work out that
then we can work out that

and

The infinitesimal transforms as

and so

thus making it clear that the metric tensor is invariant under SL(2,R).
The invariant volume element
is given by

The metric is given by


for .
.
Another interesting form of the metric can be given in terms of the cross-ratio
. Given any four points and
and  in the compactified complex plane
in the compactified complex plane
 , the cross-ratio is defined by
, the cross-ratio is defined by

Then the metric is given by

Here, and
and  are the endpoints, on the real number line, of the geodesic joining
are the endpoints, on the real number line, of the geodesic joining 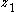 and
and  . These are numbered so that
. These are numbered so that  lies in between
lies in between 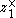 and
and  .
.
The geodesics for this metric tensor are circular arcs perpendicular to the real axis (half-circles whose origin is on the real axis) and straight vertical lines ending on the real axis.
to the unit disk with the Möbius transformation
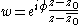
where w is the point on the unit disk that corresponds to the point z in the upper half plane. In this mapping, the constant z0 can be any point in the upper half plane; it will be mapped to the center of the disk. The real axis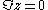 maps to the edge of the unit disk
maps to the edge of the unit disk 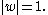 The constant real number
The constant real number 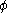 can be used to rotate the disk by an arbitrary fixed amount.
can be used to rotate the disk by an arbitrary fixed amount.
The canonical mapping is
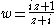
which takes i to the center of the disk, and 0 to the bottom of the disk.
is given on the open unit disk by
by

The volume element is given by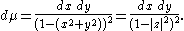
The Poincaré metric is given by
for
The geodesics for this metric tensor are circular arcs whose endpoints are orthogonal to the boundary of the disk.

 A second common mapping of the upper half-plane to a disk is the q-mapping
A second common mapping of the upper half-plane to a disk is the q-mapping

where q is the nome and τ is the half-period ratio. In the notation of the previous sections, τ is the coordinate in the upper half-plane . The mapping is to the punctured disk, because the value q=0 is not in the image
. The mapping is to the punctured disk, because the value q=0 is not in the image
of the map.
The Poincaré metric on the upper half-plane induces a metric on the q-disk

The potential of the metric is
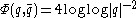
on harmonic
functions. This is an extension of the Schwarz lemma
, called the Schwarz-Alhfors-Pick theorem.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Poincaré metric, named after Henri Poincaré
Henri Poincaré
Jules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...
, is the metric tensor
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
describing a two-dimensional surface of constant negative curvature
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
. It is the natural metric commonly used in a variety of calculations in hyperbolic geometry
Hyperbolic geometry
In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
or Riemann surface
Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
s.
There are three equivalent representations commonly used in two-dimensional hyperbolic geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
. One is the Poincaré half-plane model
Poincaré half-plane model
In non-Euclidean geometry, the Poincaré half-plane model is the upper half-plane , together with a metric, the Poincaré metric, that makes it a model of two-dimensional hyperbolic geometry....
, defining a model of hyperbolic space on the upper half-plane. The Poincaré disk model
Poincaré disk model
In geometry, the Poincaré disk model, also called the conformal disk model, is a model of n-dimensional hyperbolic geometry in which the points of the geometry are in an n-dimensional disk, or unit ball, and the straight lines of the hyperbolic geometry are segments of circles contained in the disk...
defines a model for hyperbolic space on the unit disk. The disk and the upper half plane are related by a conformal map
Conformal map
In mathematics, a conformal map is a function which preserves angles. In the most common case the function is between domains in the complex plane.More formally, a map,...
, and isometries
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
are given by Mobius transformations. A third representation is on the punctured disk, where relations for q-analog
Q-analog
Roughly speaking, in mathematics, specifically in the areas of combinatorics and special functions, a q-analog of a theorem, identity or expression is a generalization involving a new parameter q that returns the original theorem, identity or expression in the limit as q → 1...
ues are sometimes expressed. These various forms are reviewed below.
Overview of metrics on Riemann surfaces
A metric on the complex plane may be generally expressed in the form
where λ is a real, positive function of z and
 . The length of a curve γ in the complex plane is thus given by
. The length of a curve γ in the complex plane is thus given by
The area of a subset of the complex plane is given by
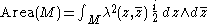
where
 is the exterior product used to construct the volume form
is the exterior product used to construct the volume formVolume form
In mathematics, a volume form on a differentiable manifold is a nowhere-vanishing differential form of top degree. Thus on a manifold M of dimension n, a volume form is an n-form, a section of the line bundle Ωn = Λn, that is nowhere equal to zero. A manifold has a volume...
. The determinant of the metric is equal to
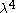 , so the square root of the determinant is
, so the square root of the determinant is  . The Euclidean volume form on the plane is
. The Euclidean volume form on the plane is  and so one has
and so one has
A function
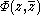 is said to be the potential of the metric if
is said to be the potential of the metric if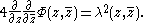
The Laplace–Beltrami operator is given by

The Gaussian curvature
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
of the metric is given by

This curvature is one-half of the Ricci scalar curvature.
Isometries preserve angles and arc-lengths. On Riemann surfaces, isometries are identical to changes of coordinate: that is, both the Laplace–Beltrami operator and the curvature are invariant under isometries. Thus, for example, let S be a Riemann surface with metric
 and T be a Riemann surface with metric
and T be a Riemann surface with metric  . Then a map
. Then a map
with
 is an isometry if and only if it is conformal and if
is an isometry if and only if it is conformal and if .
.Here, the requirement that the map is conformal is nothing more than the statement

that is,

Metric and volume element on the Poincaré plane
The Poincaré metric tensor in the Poincaré half-plane modelPoincaré half-plane model
In non-Euclidean geometry, the Poincaré half-plane model is the upper half-plane , together with a metric, the Poincaré metric, that makes it a model of two-dimensional hyperbolic geometry....
is given on the upper half-plane H as

where we write

This metric tensor is invariant under the action of SL(2,R). That is, if we write

for
 then we can work out that
then we can work out that
and

The infinitesimal transforms as

and so

thus making it clear that the metric tensor is invariant under SL(2,R).
The invariant volume element
Volume element
In mathematics, a volume element provides a means for integrating a function with respect to volume in various coordinate systems such as spherical coordinates and cylindrical coordinates...
is given by

The metric is given by


for
 .
.Another interesting form of the metric can be given in terms of the cross-ratio
Cross-ratio
In geometry, the cross-ratio, also called double ratio and anharmonic ratio, is a special number associated with an ordered quadruple of collinear points, particularly points on a projective line...
. Given any four points
 and
and  in the compactified complex plane
in the compactified complex planeRiemann sphere
In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
 , the cross-ratio is defined by
, the cross-ratio is defined by
Then the metric is given by

Here,
 and
and  are the endpoints, on the real number line, of the geodesic joining
are the endpoints, on the real number line, of the geodesic joining 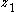 and
and  . These are numbered so that
. These are numbered so that  lies in between
lies in between 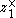 and
and  .
.The geodesics for this metric tensor are circular arcs perpendicular to the real axis (half-circles whose origin is on the real axis) and straight vertical lines ending on the real axis.
Conformal map of plane to disk
The upper half plane can be mapped conformallyConformal map
In mathematics, a conformal map is a function which preserves angles. In the most common case the function is between domains in the complex plane.More formally, a map,...
to the unit disk with the Möbius transformation
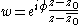
where w is the point on the unit disk that corresponds to the point z in the upper half plane. In this mapping, the constant z0 can be any point in the upper half plane; it will be mapped to the center of the disk. The real axis
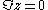 maps to the edge of the unit disk
maps to the edge of the unit disk 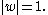 The constant real number
The constant real number 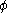 can be used to rotate the disk by an arbitrary fixed amount.
can be used to rotate the disk by an arbitrary fixed amount.The canonical mapping is
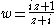
which takes i to the center of the disk, and 0 to the bottom of the disk.
Metric and volume element on the Poincaré disk
The Poincaré metric tensor in the Poincaré disk modelPoincaré disk model
In geometry, the Poincaré disk model, also called the conformal disk model, is a model of n-dimensional hyperbolic geometry in which the points of the geometry are in an n-dimensional disk, or unit ball, and the straight lines of the hyperbolic geometry are segments of circles contained in the disk...
is given on the open unit disk
 by
by
The volume element is given by
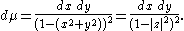
The Poincaré metric is given by

for

The geodesics for this metric tensor are circular arcs whose endpoints are orthogonal to the boundary of the disk.
The punctured disk model


Q-analog
Roughly speaking, in mathematics, specifically in the areas of combinatorics and special functions, a q-analog of a theorem, identity or expression is a generalization involving a new parameter q that returns the original theorem, identity or expression in the limit as q → 1...

where q is the nome and τ is the half-period ratio. In the notation of the previous sections, τ is the coordinate in the upper half-plane
 . The mapping is to the punctured disk, because the value q=0 is not in the image
. The mapping is to the punctured disk, because the value q=0 is not in the imageCodomain
In mathematics, the codomain or target set of a function is the set into which all of the output of the function is constrained to fall. It is the set in the notation...
of the map.
The Poincaré metric on the upper half-plane induces a metric on the q-disk

The potential of the metric is
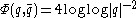
Schwarz lemma
The Poincaré metric is distance-decreasingContraction mapping
In mathematics, a contraction mapping, or contraction, on a metric space is a function f from M to itself, with the property that there is some nonnegative real number k...
on harmonic
Laplace operator
In mathematics the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a function on Euclidean space. It is usually denoted by the symbols ∇·∇, ∇2 or Δ...
functions. This is an extension of the Schwarz lemma
Schwarz lemma
In mathematics, the Schwarz lemma, named after Hermann Amandus Schwarz, is a result in complex analysis about holomorphic functions from the open unit disk to itself. The lemma is less celebrated than stronger theorems, such as the Riemann mapping theorem, which it helps to prove...
, called the Schwarz-Alhfors-Pick theorem.
See also
- Fuchsian groupFuchsian groupIn mathematics, a Fuchsian group is a discrete subgroup of PSL. The group PSL can be regarded as a group of isometries of the hyperbolic plane, or conformal transformations of the unit disc, or conformal transformations of the upper half plane, so a Fuchsian group can be regarded as a group acting...
- Fuchsian modelFuchsian modelIn mathematics, a Fuchsian model is a construction of a hyperbolic Riemann surface R as a quotient of the upper half-plane H. By the uniformization theorem, every Riemann surface is either elliptic, parabolic or hyperbolic. Every hyperbolic Riemann surface has a non-trivial fundamental group \pi_1...
- Kleinian groupKleinian groupIn mathematics, a Kleinian group is a discrete subgroup of PSL. The group PSL of 2 by 2 complex matrices of determinant 1 modulo its center has several natural representations: as conformal transformations of the Riemann sphere, and as orientation-preserving isometries of 3-dimensional hyperbolic...
- Kleinian model
- Poincaré disk modelPoincaré disk modelIn geometry, the Poincaré disk model, also called the conformal disk model, is a model of n-dimensional hyperbolic geometry in which the points of the geometry are in an n-dimensional disk, or unit ball, and the straight lines of the hyperbolic geometry are segments of circles contained in the disk...
- Poincaré half-plane modelPoincaré half-plane modelIn non-Euclidean geometry, the Poincaré half-plane model is the upper half-plane , together with a metric, the Poincaré metric, that makes it a model of two-dimensional hyperbolic geometry....
- Prime geodesicPrime geodesicIn mathematics, a prime geodesic on a hyperbolic surface is a primitive closed geodesic, i.e. a geodesic which is a closed curve that traces out its image exactly once...

