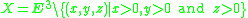_space.gif)
CAT(k) space
Encyclopedia
In mathematics
, a CAT(k) space is a specific type of metric space
. Intuitively, triangle
s in a CAT(k) space are "slimmer" than corresponding "model triangles" in a standard space of constant curvature
k. In a CAT(k) space, the curvature is bounded from above by k. A notable special case is k = 0: complete
CAT(0) spaces are known as Hadamard spaces after the French
mathematician
Jacques Hadamard
.
Originally, Alexandrov
called these spaces "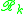 domain".
domain".
The terminology "CAT(k)" was coined by Mikhail Gromov in 1987 and is an acronym for Élie Cartan
, Aleksandr Danilovich Aleksandrov
and Victor Andreevich Toponogov
(although Toponogov was never doing curvature bounded above).
 For a real number
For a real number
k, let Mk denote the unique simply connected
surface
(real 2-dimensional Riemannian manifold
) with constant curvature k. Denote by Dk the diameter
of Mk, which is +∞ if k ≤ 0 and π/√k for k > 0.
Let (X, d) be a geodesic metric space, i.e. a metric space for which every two points x, y ∈ X can be joined by a geodesic segment, an arc length
parametrized continuous curve
γ : [a, b] → X, γ(a) = x, γ(b) = y, whose length
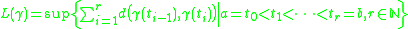
is precisely d(x, y). Let Δ be a triangle in X with geodesic segments as its sides. Δ is said to satisfy the CAT(k) inequality if there is a comparison triangle Δ′ in the model space Mk, with sides of the same length as the sides of Δ, such that distances between points on Δ are less than or equal to the distances between corresponding points on Δ′.
The geodesic metric space (X, d) is said to be a CAT(k) space if every geodesic triangle Δ in X with perimeter
less than 2Dk satisfies the CAT(k) inequality. A (not-necessarily-geodesic) metric space (X, d) is said to be a space with curvature ≤ k if every point of X has a geodesically convex
CAT(k) neighbourhood
. A space with curvature ≤ 0 may be said to have non-positive curvature
.
s. A Hadamard space is contractible
(it has the homotopy type of a single point) and, between any two points of a Hadamard space, there is a unique geodesic segment connecting them. Most importantly, distance functions in Hadamard spaces are convex
: if σ1, σ2 are two geodesics in X defined on the same interval
of time I, then the function I → R given by
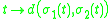
is convex in t.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a CAT(k) space is a specific type of metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
. Intuitively, triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
s in a CAT(k) space are "slimmer" than corresponding "model triangles" in a standard space of constant curvature
Constant curvature
In mathematics, constant curvature in differential geometry is a concept most commonly applied to surfaces. For those the scalar curvature is a single number determining the local geometry, and its constancy has the obvious meaning that it is the same at all points...
k. In a CAT(k) space, the curvature is bounded from above by k. A notable special case is k = 0: complete
Complete space
In mathematical analysis, a metric space M is called complete if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in M converges in M....
CAT(0) spaces are known as Hadamard spaces after the French
France
The French Republic , The French Republic , The French Republic , (commonly known as France , is a unitary semi-presidential republic in Western Europe with several overseas territories and islands located on other continents and in the Indian, Pacific, and Atlantic oceans. Metropolitan France...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Jacques Hadamard
Jacques Hadamard
Jacques Salomon Hadamard FRS was a French mathematician who made major contributions in number theory, complex function theory, differential geometry and partial differential equations.-Biography:...
.
Originally, Alexandrov
Aleksandr Danilovich Aleksandrov
Aleksandr Danilovich Aleksandrov , and Alexandrov ) , was a Soviet/Russian mathematician, physicist, philosopher and mountaineer.- Scientific career :...
called these spaces "
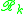 domain".
domain".The terminology "CAT(k)" was coined by Mikhail Gromov in 1987 and is an acronym for Élie Cartan
Élie Cartan
Élie Joseph Cartan was an influential French mathematician, who did fundamental work in the theory of Lie groups and their geometric applications...
, Aleksandr Danilovich Aleksandrov
Aleksandr Danilovich Aleksandrov
Aleksandr Danilovich Aleksandrov , and Alexandrov ) , was a Soviet/Russian mathematician, physicist, philosopher and mountaineer.- Scientific career :...
and Victor Andreevich Toponogov
Victor Andreevich Toponogov
Victor Andreevich Toponogov was a Russian mathematician, noted for his contributions to differential geometry and so-called Riemannian geometry "in the large"....
(although Toponogov was never doing curvature bounded above).
Definitions

Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
k, let Mk denote the unique simply connected
Simply connected space
In topology, a topological space is called simply connected if it is path-connected and every path between two points can be continuously transformed, staying within the space, into any other path while preserving the two endpoints in question .If a space is not simply connected, it is convenient...
surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
(real 2-dimensional Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
) with constant curvature k. Denote by Dk the diameter
Diameter
In geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints are on the circle. The diameters are the longest chords of the circle...
of Mk, which is +∞ if k ≤ 0 and π/√k for k > 0.
Let (X, d) be a geodesic metric space, i.e. a metric space for which every two points x, y ∈ X can be joined by a geodesic segment, an arc length
Arc length
Determining the length of an irregular arc segment is also called rectification of a curve. Historically, many methods were used for specific curves...
parametrized continuous curve
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
γ : [a, b] → X, γ(a) = x, γ(b) = y, whose length
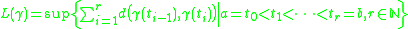
is precisely d(x, y). Let Δ be a triangle in X with geodesic segments as its sides. Δ is said to satisfy the CAT(k) inequality if there is a comparison triangle Δ′ in the model space Mk, with sides of the same length as the sides of Δ, such that distances between points on Δ are less than or equal to the distances between corresponding points on Δ′.
The geodesic metric space (X, d) is said to be a CAT(k) space if every geodesic triangle Δ in X with perimeter
Perimeter
A perimeter is a path that surrounds an area. The word comes from the Greek peri and meter . The term may be used either for the path or its length - it can be thought of as the length of the outline of a shape. The perimeter of a circular area is called circumference.- Practical uses :Calculating...
less than 2Dk satisfies the CAT(k) inequality. A (not-necessarily-geodesic) metric space (X, d) is said to be a space with curvature ≤ k if every point of X has a geodesically convex
Geodesic convexity
In mathematics — specifically, in Riemannian geometry — geodesic convexity is a natural generalization of convexity for sets and functions to Riemannian manifolds...
CAT(k) neighbourhood
Neighbourhood (mathematics)
In topology and related areas of mathematics, a neighbourhood is one of the basic concepts in a topological space. Intuitively speaking, a neighbourhood of a point is a set containing the point where you can move that point some amount without leaving the set.This concept is closely related to the...
. A space with curvature ≤ 0 may be said to have non-positive curvature
Non-positive curvature
In mathematics, spaces of non-positive curvature occur in many contexts and form a generalization of hyperbolic geometry. In the category of Riemannian manifolds, one can consider the sectional curvature of the manifold and require that this curvature be everywhere less than or equal to zero...
.
Examples
- Any CAT(k) space (X, d) is also a CAT(ℓ) space for all ℓ > k. In fact, the converse holds: if (X, d) is a CAT(ℓ) space for all ℓ > k, then it is a CAT(k) space.
- n-dimensional Euclidean spaceEuclidean spaceIn mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
En with its usual metric is a CAT(0) space. More generally, any real inner product spaceInner product spaceIn mathematics, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors...
(not necessarily complete) is a CAT(0) space; conversely, if a real normed vector spaceNormed vector spaceIn mathematics, with 2- or 3-dimensional vectors with real-valued entries, the idea of the "length" of a vector is intuitive and can easily be extended to any real vector space Rn. The following properties of "vector length" are crucial....
is a CAT(k) space for some real k, then it is an inner product space. - n-dimensional hyperbolic spaceHyperbolic spaceIn mathematics, hyperbolic space is a type of non-Euclidean geometry. Whereas spherical geometry has a constant positive curvature, hyperbolic geometry has a negative curvature: every point in hyperbolic space is a saddle point...
Hn with its usual metric is a CAT(−1) space, and hence a CAT(0) space as well. - The n-dimensional unit sphereUnit sphereIn mathematics, a unit sphere is the set of points of distance 1 from a fixed central point, where a generalized concept of distance may be used; a closed unit ball is the set of points of distance less than or equal to 1 from a fixed central point...
Sn is a CAT(1) space. - More generally, the standard space Mk is a CAT(k) space. So, for example, regardless of dimension, the sphere of radius r (and constant curvature 1/√r) is a CAT(1/√r) space. Note that the diameter of the sphere is πr (as measured on the surface of the sphere) not 2r (as measured by going through the centre of the sphere).
- The punctured plane Π = E2 \ {0} is not a CAT(0) space since it is not geodesically convex (for example, the points (0, 1) and (0, −1) cannot be joined by a geodesic in Π with arc length 2), but every point of Π does have a CAT(0) geodesically convex neighbourhood, so Π is a space of curvature ≤ 0.
- The closed subspace X of E3 given by
- equipped with the induced length metric is not a CAT(k) space for any k.
- Any product of CAT(0) spaces is CAT(0). (This does not hold for negative arguments.)
Hadamard spaces
As a special case, a complete CAT(0) space is also known as a Hadamard space; this is by analogy with the situation for Hadamard manifoldHadamard manifold
In mathematics, a Hadamard manifold, named after Jacques Hadamard — sometimes called a Cartan–Hadamard manifold, after Élie Cartan — is a Riemannian manifold that is complete and simply-connected, and has everywhere non-positive sectional curvature.-Examples:* The real line R with its...
s. A Hadamard space is contractible
Contractible space
In mathematics, a topological space X is contractible if the identity map on X is null-homotopic, i.e. if it is homotopic to some constant map. Intuitively, a contractible space is one that can be continuously shrunk to a point....
(it has the homotopy type of a single point) and, between any two points of a Hadamard space, there is a unique geodesic segment connecting them. Most importantly, distance functions in Hadamard spaces are convex
Convex function
In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
: if σ1, σ2 are two geodesics in X defined on the same interval
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
of time I, then the function I → R given by
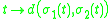
is convex in t.
Properties of CAT(k) spaces
Let (X, d) be a CAT(k) space. Then the following properties hold:- Given any two points x, y ∈ X (with d(x, y) < Dk if k > 0), there is a unique geodesic segment that joins x to y; moreover, this segment varies continuously as a function of its endpoints.
- Every local geodesic in X with length at most Dk is a geodesic.
- The d-balls in X of radius less than ½Dk are (geodesically) convex.
- The d-balls in X of radius less than Dk are contractible.
- Approximate mid-points are close to mid-points in the following sense: for every λ < Dk and every ε > 0, there exists a δ = δ(k, λ, ε) > 0 such that, if m is the mid-point of a geodesic segment from x to y with d(x, y) ≤ λ and
- then d(m, m′) < ε.
- It follows from these properties that, for k ≤ 0, the universal cover of every CAT(k) space is contractible; in particular, the higher homotopy groupHomotopy groupIn mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, which records information about loops in a space...
s of such a space are trivialTrivial groupIn mathematics, a trivial group is a group consisting of a single element. All such groups are isomorphic so one often speaks of the trivial group. The single element of the trivial group is the identity element so it usually denoted as such, 0, 1 or e depending on the context...
. As the example of the n-sphere Sn shows, there is, in general, no hope for a CAT(k) space to be contractible if k is strictly positive.