
Upper half-plane
Encyclopedia
In mathematics
, the upper half-plane H is the set of complex number
s with positive imaginary part y:
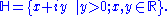
The term is associated with a common visualization of complex numbers with points in the plane endowed with Cartesian coordinates, with the Y-axis pointing upwards: the "upper half-plane" corresponds to the half-plane above the X-axis.
It is the domain
of many functions of interest in complex analysis
, especially modular form
s. The lower half-plane, defined by y < 0, is equally good, but less used by convention. The open unit disk D (the set of all complex numbers of absolute value
less than one) is equivalent by a conformal mapping (see "Poincaré metric
"), meaning that it is usually possible to pass between H and D.
It also plays an important role in hyperbolic geometry
, where the Poincaré half-plane model
provides a way of examining hyperbolic motion
s. The Poincaré metric provides a hyperbolic metric
on the space.
The uniformization theorem
for surface
s states that the upper half-plane is the universal covering space of surfaces with constant negative Gaussian curvature
.
Hn, the maximally symmetric, simply connected, n-dimensional Riemannian manifold
with constant sectional curvature
−1. In this terminology, the upper half-plane is H2 since it has real dimension
2.
In number theory
, the theory of Hilbert modular forms is concerned with the study of certain functions on the direct product Hn of n copies of the upper half-plane. Yet another space interesting to number theorists is the Siegel upper half-space Hn, which is the domain
of Siegel modular form
s.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the upper half-plane H is the set of complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s with positive imaginary part y:
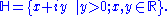
The term is associated with a common visualization of complex numbers with points in the plane endowed with Cartesian coordinates, with the Y-axis pointing upwards: the "upper half-plane" corresponds to the half-plane above the X-axis.
It is the domain
Domain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
of many functions of interest in complex analysis
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
, especially modular form
Modular form
In mathematics, a modular form is a analytic function on the upper half-plane satisfying a certain kind of functional equation and growth condition. The theory of modular forms therefore belongs to complex analysis but the main importance of the theory has traditionally been in its connections...
s. The lower half-plane, defined by y < 0, is equally good, but less used by convention. The open unit disk D (the set of all complex numbers of absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
less than one) is equivalent by a conformal mapping (see "Poincaré metric
Poincaré metric
In mathematics, the Poincaré metric, named after Henri Poincaré, is the metric tensor describing a two-dimensional surface of constant negative curvature. It is the natural metric commonly used in a variety of calculations in hyperbolic geometry or Riemann surfaces.There are three equivalent...
"), meaning that it is usually possible to pass between H and D.
It also plays an important role in hyperbolic geometry
Hyperbolic geometry
In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
, where the Poincaré half-plane model
Poincaré half-plane model
In non-Euclidean geometry, the Poincaré half-plane model is the upper half-plane , together with a metric, the Poincaré metric, that makes it a model of two-dimensional hyperbolic geometry....
provides a way of examining hyperbolic motion
Hyperbolic motion
In geometry, hyperbolic motions are isometric automorphisms of a hyperbolic space. Under composition of mappings, the hyperbolic motions form a continuous group. This group is said to characterize the hyperbolic space. Such an approach to geometry was cultivated by Felix Klein in his Erlangen program...
s. The Poincaré metric provides a hyperbolic metric
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
on the space.
The uniformization theorem
Uniformization theorem
In mathematics, the uniformization theorem says that any simply connected Riemann surface is conformally equivalent to one of the three domains: the open unit disk, the complex plane, or the Riemann sphere. In particular it admits a Riemannian metric of constant curvature...
for surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
s states that the upper half-plane is the universal covering space of surfaces with constant negative Gaussian curvature
Gaussian curvature
In differential geometry, the Gaussian curvature or Gauss curvature of a point on a surface is the product of the principal curvatures, κ1 and κ2, of the given point. It is an intrinsic measure of curvature, i.e., its value depends only on how distances are measured on the surface, not on the way...
.
Generalizations
One natural generalization in differential geometry is hyperbolic n-spaceHyperbolic space
In mathematics, hyperbolic space is a type of non-Euclidean geometry. Whereas spherical geometry has a constant positive curvature, hyperbolic geometry has a negative curvature: every point in hyperbolic space is a saddle point...
Hn, the maximally symmetric, simply connected, n-dimensional Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
with constant sectional curvature
Sectional curvature
In Riemannian geometry, the sectional curvature is one of the ways to describe the curvature of Riemannian manifolds. The sectional curvature K depends on a two-dimensional plane σp in the tangent space at p...
−1. In this terminology, the upper half-plane is H2 since it has real dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
2.
In number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, the theory of Hilbert modular forms is concerned with the study of certain functions on the direct product Hn of n copies of the upper half-plane. Yet another space interesting to number theorists is the Siegel upper half-space Hn, which is the domain
Domain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
of Siegel modular form
Siegel modular form
In mathematics, Siegel modular forms are a major type of automorphic form. These stand in relation to the conventional elliptic modular forms as abelian varieties do in relation to elliptic curves; the complex manifolds constructed as in the theory are basic models for what a moduli space for...
s.
See also
- Cusp neighborhoodCusp neighborhoodIn mathematics, a cusp neighborhood is defined as a set of points near a cusp.-Cusp neighborhood for a Riemann surface:The cusp neighborhood for a hyperbolic Riemann surface can be defined in terms of its Fuchsian model....
- Extended complex upper-half plane
- Fuchsian groupFuchsian groupIn mathematics, a Fuchsian group is a discrete subgroup of PSL. The group PSL can be regarded as a group of isometries of the hyperbolic plane, or conformal transformations of the unit disc, or conformal transformations of the upper half plane, so a Fuchsian group can be regarded as a group acting...
- Fundamental domainFundamental domainIn geometry, the fundamental domain of a symmetry group of an object is a part or pattern, as small or irredundant as possible, which determines the whole object based on the symmetry. More rigorously, given a topological space and a group acting on it, the images of a single point under the group...
- Hyperbolic geometryHyperbolic geometryIn mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
- Kleinian groupKleinian groupIn mathematics, a Kleinian group is a discrete subgroup of PSL. The group PSL of 2 by 2 complex matrices of determinant 1 modulo its center has several natural representations: as conformal transformations of the Riemann sphere, and as orientation-preserving isometries of 3-dimensional hyperbolic...
- Modular groupModular groupIn mathematics, the modular group Γ is a fundamental object of study in number theory, geometry, algebra, and many other areas of advanced mathematics...
- Riemann surfaceRiemann surfaceIn mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
- Schwarz-Ahlfors-Pick theorem

