
Willmore conjecture
Encyclopedia
In differential geometry in mathematics
the Willmore conjecture is a conjecture
about the Willmore energy
of a torus
, named after the English
mathematician
Tom Willmore
.
immersion of a compact
, orientable surface
(of dimension
two). Giving M the Riemannian metric induced by v, let H : M → R be the mean curvature
(the arithmetic mean
of the principal curvature
s κ1 and κ2 at each point). In this notation, the Willmore energy W(M) of M is given by
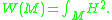
It is not hard to prove that the Willmore energy satisfies W(M) ≥ 4π, with equality if and only if
M is an embedded round sphere
. Calculation of W(M) for a few examples suggests that there should be a better bound for surfaces with genus g(M) > 0. In particular, calculation of W(M) for tori with various symmetries led Willmore to propose in 1965 the following conjecture, which now bears his name: for any smooth immersed torus M in R3, W(M) ≥ 2π2.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
the Willmore conjecture is a conjecture
Conjecture
A conjecture is a proposition that is unproven but is thought to be true and has not been disproven. Karl Popper pioneered the use of the term "conjecture" in scientific philosophy. Conjecture is contrasted by hypothesis , which is a testable statement based on accepted grounds...
about the Willmore energy
Willmore energy
In differential geometry, the Willmore energy is a quantitative measure of how much a given surface deviates from a round sphere. Mathematically, the Willmore energy of a smooth closed surface embedded in three-dimensional Euclidean space is defined to be the integral of the mean curvature squared...
of a torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
, named after the English
England
England is a country that is part of the United Kingdom. It shares land borders with Scotland to the north and Wales to the west; the Irish Sea is to the north west, the Celtic Sea to the south west, with the North Sea to the east and the English Channel to the south separating it from continental...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Tom Willmore
Tom Willmore
Thomas James Willmore was an English geometer. He is best known for his work on Riemannian 3-space and harmonic spaces.Willmore studied at King's College London...
.
Statement of the conjecture
Let v : M → R3 be a smoothSmooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
immersion of a compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
, orientable surface
Orientability
In mathematics, orientability is a property of surfaces in Euclidean space measuring whether or not it is possible to make a consistent choice of surface normal vector at every point. A choice of surface normal allows one to use the right-hand rule to define a "clockwise" direction of loops in the...
(of dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
two). Giving M the Riemannian metric induced by v, let H : M → R be the mean curvature
Mean curvature
In mathematics, the mean curvature H of a surface S is an extrinsic measure of curvature that comes from differential geometry and that locally describes the curvature of an embedded surface in some ambient space such as Euclidean space....
(the arithmetic mean
Arithmetic mean
In mathematics and statistics, the arithmetic mean, often referred to as simply the mean or average when the context is clear, is a method to derive the central tendency of a sample space...
of the principal curvature
Principal curvature
In differential geometry, the two principal curvatures at a given point of a surface are the eigenvalues of the shape operator at the point. They measure how the surface bends by different amounts in different directions at that point.-Discussion:...
s κ1 and κ2 at each point). In this notation, the Willmore energy W(M) of M is given by
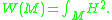
It is not hard to prove that the Willmore energy satisfies W(M) ≥ 4π, with equality if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
M is an embedded round sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
. Calculation of W(M) for a few examples suggests that there should be a better bound for surfaces with genus g(M) > 0. In particular, calculation of W(M) for tori with various symmetries led Willmore to propose in 1965 the following conjecture, which now bears his name: for any smooth immersed torus M in R3, W(M) ≥ 2π2.

