Carl Gustav Jakob Jacobi
Encyclopedia
Carl Gustav Jacob Jacobi (December 10, 1804 – February 18, 1851) was a German
mathematician
, widely considered to be the most inspiring teacher of his time and is considered one of the greatest mathematicians of his generation.
. From 1816 to 1821 Jacobi went to the Victoria-Gymnasium, where he went to the senior classes right from the beginning, but still had to stay for several years. He studied at Berlin University, where he obtained the degree of Doctor of Philosophy
in 1825, his thesis being an analytical discussion of the theory of fraction
s. In 1827 he became a professor
and in 1829, a Tenured professor of Mathematics
at Königsberg University, and held the chair until 1842.
Jacobi suffered a breakdown
from overwork in 1843. He then visited Italy
for a few months to regain his health. On his return he moved to Berlin
, where he lived as a royal pensioner until his death. During the Revolution of 1848 Jacobi was politically involved and unsuccessfully presented his parliamentary candidature on behalf of a Liberal
club. This led, after the suppression of the revolution, to his royal grant being cut off – but his fame and reputation were such that it was soon resumed. In 1836, he had been elected a foreign member of the Royal Swedish Academy of Sciences
.
Jacobi's grave is preserved at a cemetery in the Kreuzberg
section of Berlin, the Friedhof I der Dreifaltigkeits-Kirchengemeinde (61 Baruther Street). His grave is close to that of Johann Encke, the astronomer. The crater Jacobi
on the Moon
is named after him.
s and their relation to the elliptic theta function. This was developed in his great treatise Fundamenta nova theoriae functionum ellipticarum (1829), and in later papers in Crelle's Journal
. Theta functions are of great importance in mathematical physics because of their role in the inverse problem for periodic and quasi-periodic flows. The equations of motion are integrable
in terms of Jacobi's elliptic functions
in the well-known cases of the pendulum
, the Euler top, the symmetric Lagrange
top in a gravitational field
and the Kepler problem (planetary motion in a central gravitational field).
He also made fundamental contributions in the study of differential equations and to rational mechanics, notably the Hamilton–Jacobi theory
.
It was in algebraic development that Jacobi’s peculiar power mainly lay, and he made important contributions of this kind to many areas of mathematics, as shown by his long list of papers in Crelle’s Journal and elsewhere from 1826 onwards. One of his maxims was: 'Invert, always invert' ('man muss immer umkehren'), expressing his belief that the solution of many hard problems can be clarified by re-expressing them in inverse form.
In his 1835 paper, Jacobi proved the following basic result classifying periodic (including elliptic) functions:
If a univariate single-value function is multiply periodic
, then such a function cannot have more than two periods, and the ratio of the periods cannot be a real number
.
He discovered many of the fundamental properties of theta functions, including the functional equation and the Jacobi triple product formula,
as well as many other results on q-series and hypergeometric series
.
The solution of the Jacobi inversion problem for the hyperelliptic Abel map by Weierstrass in 1854 required the introduction of the hyperelliptic theta function and later the general Riemann theta function for algebraic curves of arbitrary genus. The complex torus associated to a genus
algebraic curve, obtained by quotienting 
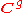by the lattice of periods is referred to as the Jacobian variety
. This method of inversion, and its subsequent extension by Weierstrass and Riemann to arbitrary algebraic curves, may be seen as a higher genus generalization of the relation between elliptic integrals and the Jacobi, or Weierstrass elliptic functions
Jacobi was the first to apply elliptic functions to number theory
, for example proving of Fermat's
two-square theorem and Lagrange's
four-square theorem
, and similar results for 6 and 8 squares.
His other work in number theory continued the work of C. F. Gauss: new proofs of quadratic reciprocity
and introduction of the Jacobi symbol
; contributions to higher reciprocity laws, investigations of continued fractions, and the invention of Jacobi sum
s.
He was also one of the early founders of the theory of determinants; in particular, he invented the Jacobian determinant formed from the n² differential coefficients of n given functions of n independent variables, and which has played an important part in many analytical investigations. In 1841 he reintroduced the partial derivative
∂ notation of Legendre
, which was to become standard.
Students of vector fields and Lie theory
often encounter the Jacobi identity
, the analog of associativity for the Lie bracket
operation.
Planetary theory and other particular dynamical problems likewise occupied his attention from time to time. While contributing to celestial mechanics
, he introduced the Jacobi integral
(1836) for a sidereal coordinate system. His theory of the last multiplier is treated in Vorlesungen über Dynamik, edited by Alfred Clebsch
(1866).
He reduced the general quintic equation
to the form: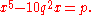
He left a vast store of manuscripts, portions of which have been published at intervals in Crelle's Journal. His other works include Commentatio de transformatione integralis duplicis indefiniti in formam simpliciorem (1832), Canon arithmeticus (1839), and Opuscula mathematica (1846–1857). His Gesammelte Werke (1881–1891) were published by the Berlin Academy.
Germany
Germany , officially the Federal Republic of Germany , is a federal parliamentary republic in Europe. The country consists of 16 states while the capital and largest city is Berlin. Germany covers an area of 357,021 km2 and has a largely temperate seasonal climate...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
, widely considered to be the most inspiring teacher of his time and is considered one of the greatest mathematicians of his generation.
Biography
Jacobi was born of Jewish parentage in PotsdamPotsdam
Potsdam is the capital city of the German federal state of Brandenburg and part of the Berlin/Brandenburg Metropolitan Region. It is situated on the River Havel, southwest of Berlin city centre....
. From 1816 to 1821 Jacobi went to the Victoria-Gymnasium, where he went to the senior classes right from the beginning, but still had to stay for several years. He studied at Berlin University, where he obtained the degree of Doctor of Philosophy
Doctor of Philosophy
Doctor of Philosophy, abbreviated as Ph.D., PhD, D.Phil., or DPhil , in English-speaking countries, is a postgraduate academic degree awarded by universities...
in 1825, his thesis being an analytical discussion of the theory of fraction
Fraction (mathematics)
A fraction represents a part of a whole or, more generally, any number of equal parts. When spoken in everyday English, we specify how many parts of a certain size there are, for example, one-half, five-eighths and three-quarters.A common or "vulgar" fraction, such as 1/2, 5/8, 3/4, etc., consists...
s. In 1827 he became a professor
Professor
A professor is a scholarly teacher; the precise meaning of the term varies by country. Literally, professor derives from Latin as a "person who professes" being usually an expert in arts or sciences; a teacher of high rank...
and in 1829, a Tenured professor of Mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
at Königsberg University, and held the chair until 1842.
Jacobi suffered a breakdown
Mental breakdown
Mental breakdown is a non-medical term used to describe an acute, time-limited phase of a specific disorder that presents primarily with features of depression or anxiety.-Definition:...
from overwork in 1843. He then visited Italy
Italy
Italy , officially the Italian Republic languages]] under the European Charter for Regional or Minority Languages. In each of these, Italy's official name is as follows:;;;;;;;;), is a unitary parliamentary republic in South-Central Europe. To the north it borders France, Switzerland, Austria and...
for a few months to regain his health. On his return he moved to Berlin
Berlin
Berlin is the capital city of Germany and is one of the 16 states of Germany. With a population of 3.45 million people, Berlin is Germany's largest city. It is the second most populous city proper and the seventh most populous urban area in the European Union...
, where he lived as a royal pensioner until his death. During the Revolution of 1848 Jacobi was politically involved and unsuccessfully presented his parliamentary candidature on behalf of a Liberal
Liberalism
Liberalism is the belief in the importance of liberty and equal rights. Liberals espouse a wide array of views depending on their understanding of these principles, but generally, liberals support ideas such as constitutionalism, liberal democracy, free and fair elections, human rights,...
club. This led, after the suppression of the revolution, to his royal grant being cut off – but his fame and reputation were such that it was soon resumed. In 1836, he had been elected a foreign member of the Royal Swedish Academy of Sciences
Royal Swedish Academy of Sciences
The Royal Swedish Academy of Sciences or Kungliga Vetenskapsakademien is one of the Royal Academies of Sweden. The Academy is an independent, non-governmental scientific organization which acts to promote the sciences, primarily the natural sciences and mathematics.The Academy was founded on 2...
.
Jacobi's grave is preserved at a cemetery in the Kreuzberg
Kreuzberg
Kreuzberg, a part of the combined Friedrichshain-Kreuzberg borough located south of Mitte since 2001, is one of the best-known areas of Berlin...
section of Berlin, the Friedhof I der Dreifaltigkeits-Kirchengemeinde (61 Baruther Street). His grave is close to that of Johann Encke, the astronomer. The crater Jacobi
Jacobi (crater)
Jacobi is a lunar crater that is located in the southern highlands on the near side of the Moon. It lies southeast of the crater Lilius, with Cuvier to the north-northwest and Baco to the northeast. The crater is 68 kilometers in diameter and 3.3 kilometers in depth...
on the Moon
Moon
The Moon is Earth's only known natural satellite,There are a number of near-Earth asteroids including 3753 Cruithne that are co-orbital with Earth: their orbits bring them close to Earth for periods of time but then alter in the long term . These are quasi-satellites and not true moons. For more...
is named after him.
Scientific contributions
One of Jacobi's greatest accomplishments was his theory of elliptic functionElliptic function
In complex analysis, an elliptic function is a function defined on the complex plane that is periodic in two directions and at the same time is meromorphic...
s and their relation to the elliptic theta function. This was developed in his great treatise Fundamenta nova theoriae functionum ellipticarum (1829), and in later papers in Crelle's Journal
Crelle's Journal
Crelle's Journal, or just Crelle, is the common name for a mathematics journal, the Journal für die reine und angewandte Mathematik .- History :...
. Theta functions are of great importance in mathematical physics because of their role in the inverse problem for periodic and quasi-periodic flows. The equations of motion are integrable
Jacobi integral
In celestial mechanics, Jacobi's integral is the only known conserved quantity for the restricted three-body problem problem [1]; unlike in the two-body problem, the energy and momentum of the system are not conserved separately and a general analytical solution is not possible...
in terms of Jacobi's elliptic functions
Jacobi's elliptic functions
In mathematics, the Jacobi elliptic functions are a set of basic elliptic functions, and auxiliary theta functions, that have historical importance with also many features that show up important structure, and have direct relevance to some applications...
in the well-known cases of the pendulum
Pendulum
A pendulum is a weight suspended from a pivot so that it can swing freely. When a pendulum is displaced from its resting equilibrium position, it is subject to a restoring force due to gravity that will accelerate it back toward the equilibrium position...
, the Euler top, the symmetric Lagrange
Lagrange
La Grange literally means the barn in French. Lagrange may refer to:- People :* Charles Varlet de La Grange , French actor* Georges Lagrange , translator to and writer in Esperanto...
top in a gravitational field
Gravitational field
The gravitational field is a model used in physics to explain the existence of gravity. In its original concept, gravity was a force between point masses...
and the Kepler problem (planetary motion in a central gravitational field).
He also made fundamental contributions in the study of differential equations and to rational mechanics, notably the Hamilton–Jacobi theory
Hamilton–Jacobi equation
In mathematics, the Hamilton–Jacobi equation is a necessary condition describing extremal geometry in generalizations of problems from the calculus of variations. In physics, the Hamilton–Jacobi equation is a reformulation of classical mechanics and, thus, equivalent to other formulations such as...
.
It was in algebraic development that Jacobi’s peculiar power mainly lay, and he made important contributions of this kind to many areas of mathematics, as shown by his long list of papers in Crelle’s Journal and elsewhere from 1826 onwards. One of his maxims was: 'Invert, always invert' ('man muss immer umkehren'), expressing his belief that the solution of many hard problems can be clarified by re-expressing them in inverse form.
In his 1835 paper, Jacobi proved the following basic result classifying periodic (including elliptic) functions:
If a univariate single-value function is multiply periodic
Periodic function
In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...
, then such a function cannot have more than two periods, and the ratio of the periods cannot be a real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
.
He discovered many of the fundamental properties of theta functions, including the functional equation and the Jacobi triple product formula,
as well as many other results on q-series and hypergeometric series
Hypergeometric series
In mathematics, a generalized hypergeometric series is a series in which the ratio of successive coefficients indexed by n is a rational function of n. The series, if convergent, defines a generalized hypergeometric function, which may then be defined over a wider domain of the argument by...
.
The solution of the Jacobi inversion problem for the hyperelliptic Abel map by Weierstrass in 1854 required the introduction of the hyperelliptic theta function and later the general Riemann theta function for algebraic curves of arbitrary genus. The complex torus associated to a genus
algebraic curve, obtained by quotienting 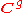by the lattice of periods is referred to as the Jacobian varietyJacobian variety
In mathematics, the Jacobian variety J of a non-singular algebraic curve C of genus g is the moduli space of degree 0 line bundles...
. This method of inversion, and its subsequent extension by Weierstrass and Riemann to arbitrary algebraic curves, may be seen as a higher genus generalization of the relation between elliptic integrals and the Jacobi, or Weierstrass elliptic functions
Jacobi was the first to apply elliptic functions to number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, for example proving of Fermat's
Pierre de Fermat
Pierre de Fermat was a French lawyer at the Parlement of Toulouse, France, and an amateur mathematician who is given credit for early developments that led to infinitesimal calculus, including his adequality...
two-square theorem and Lagrange's
Lagrange
La Grange literally means the barn in French. Lagrange may refer to:- People :* Charles Varlet de La Grange , French actor* Georges Lagrange , translator to and writer in Esperanto...
four-square theorem
Lagrange's four-square theorem
Lagrange's four-square theorem, also known as Bachet's conjecture, states that any natural number can be represented as the sum of four integer squaresp = a_0^2 + a_1^2 + a_2^2 + a_3^2\ where the four numbers are integers...
, and similar results for 6 and 8 squares.
His other work in number theory continued the work of C. F. Gauss: new proofs of quadratic reciprocity
Quadratic reciprocity
In number theory, the law of quadratic reciprocity is a theorem about modular arithmetic which gives conditions for the solvability of quadratic equations modulo prime numbers...
and introduction of the Jacobi symbol
Jacobi symbol
The Jacobi symbol is a generalization of the Legendre symbol. Introduced by Jacobi in 1837, it is of theoretical interest in modular arithmetic and other branches of number theory, but its main use is in computational number theory, especially primality testing and integer factorization; these in...
; contributions to higher reciprocity laws, investigations of continued fractions, and the invention of Jacobi sum
Jacobi sum
In mathematics, a Jacobi sum is a type of character sum formed with Dirichlet characters. Simple examples would be Jacobi sums J for Dirichlet characters \chi, \psi modulo a prime number p, defined by...
s.
He was also one of the early founders of the theory of determinants; in particular, he invented the Jacobian determinant formed from the n² differential coefficients of n given functions of n independent variables, and which has played an important part in many analytical investigations. In 1841 he reintroduced the partial derivative
Partial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
∂ notation of Legendre
Adrien-Marie Legendre
Adrien-Marie Legendre was a French mathematician.The Moon crater Legendre is named after him.- Life :...
, which was to become standard.
Students of vector fields and Lie theory
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
often encounter the Jacobi identity
Jacobi identity
In mathematics the Jacobi identity is a property that a binary operation can satisfy which determines how the order of evaluation behaves for the given operation. Unlike for associative operations, order of evaluation is significant for operations satisfying Jacobi identity...
, the analog of associativity for the Lie bracket
Lie bracket
Lie bracket can refer to:*A bilinear binary operation defined on elements of a Lie algebra*Lie bracket of vector fields...
operation.
Planetary theory and other particular dynamical problems likewise occupied his attention from time to time. While contributing to celestial mechanics
Celestial mechanics
Celestial mechanics is the branch of astronomy that deals with the motions of celestial objects. The field applies principles of physics, historically classical mechanics, to astronomical objects such as stars and planets to produce ephemeris data. Orbital mechanics is a subfield which focuses on...
, he introduced the Jacobi integral
Jacobi integral
In celestial mechanics, Jacobi's integral is the only known conserved quantity for the restricted three-body problem problem [1]; unlike in the two-body problem, the energy and momentum of the system are not conserved separately and a general analytical solution is not possible...
(1836) for a sidereal coordinate system. His theory of the last multiplier is treated in Vorlesungen über Dynamik, edited by Alfred Clebsch
Alfred Clebsch
Rudolf Friedrich Alfred Clebsch was a German mathematician who made important contributions to algebraic geometry and invariant theory. He attended the University of Königsberg and was habilitated at Berlin. He subsequently taught in Berlin and Karlsruhe...
(1866).
He reduced the general quintic equation
Quintic equation
In mathematics, a quintic function is a function of the formg=ax^5+bx^4+cx^3+dx^2+ex+f,\,where a, b, c, d, e and f are members of a field, typically the rational numbers, the real numbers or the complex numbers, and a is nonzero...
to the form:
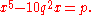
He left a vast store of manuscripts, portions of which have been published at intervals in Crelle's Journal. His other works include Commentatio de transformatione integralis duplicis indefiniti in formam simpliciorem (1832), Canon arithmeticus (1839), and Opuscula mathematica (1846–1857). His Gesammelte Werke (1881–1891) were published by the Berlin Academy.
See also
- Abel-Jacobi theorem, a statement about the Jacobian varietyJacobian varietyIn mathematics, the Jacobian variety J of a non-singular algebraic curve C of genus g is the moduli space of degree 0 line bundles...
of a curve - Jacobi's formulaJacobi's formulaIn matrix calculus, Jacobi's formula expresses the derivative of the determinant of a matrix A in terms of the adjugate of A and the derivative of A...
- Jacobi fieldJacobi fieldIn Riemannian geometry, a Jacobi field is a vector field along a geodesic \gamma in a Riemannian manifold describing the difference between the geodesic and an "infinitesimally close" geodesic. In other words, the Jacobi fields along a geodesic form the tangent space to the geodesic in the space...
- Jacobi polynomialsJacobi polynomialsIn mathematics, Jacobi polynomials are a class of classical orthogonal polynomials. They are orthogonal with respect to the weight ^\alpha ^\beta on the interval [-1, 1]...
- Carathéodory–Jacobi–Lie theorem
- Jacobi methodJacobi methodIn numerical linear algebra, the Jacobi method is an algorithm for determining the solutions of a system of linear equations with largest absolute values in each row and column dominated by the diagonal element. Each diagonal element is solved for, and an approximate value plugged in. The process...
- Jacobi eigenvalue algorithmJacobi eigenvalue algorithmIn numerical linear algebra, the Jacobi eigenvalue algorithm is an iterative method for the calculation of the eigenvalues and eigenvectors of a real symmetric matrix...
- Jacobi rotation
- Jacobi form
- Jacobian matrix and determinant