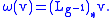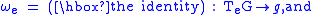Maurer-Cartan form
Encyclopedia
In mathematics
, the Maurer–Cartan form for a Lie group
G is a distinguished differential one-form
on G that carries the basic infinitesimal information about the structure of G. It was much used by Élie Cartan
as a basic ingredient of his method of moving frames, and bears his name together with that of Ludwig Maurer
.
As a one-form, the Maurer–Cartan form is peculiar in that it takes its values in the Lie algebra
associated to the Lie group G. The Lie algebra is identified with the tangent space
of G at the identity, denoted TeG. The Maurer–Cartan form ω is thus a one-form defined globally on G which is a linear mapping of the tangent space TgG at each g ∈ G into TeG. It is given as the pushforward of a vector in TgG along the left-translation in the group: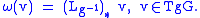
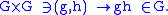
A question of importance to Cartan and his contemporaries was how to identify a principal homogeneous space
of G. That is, a manifold
P identical to the group G, but without a fixed choice of unit element. This motivation came, in part, from Felix Klein
's Erlangen programme where one was interested in a notion of symmetry
on a space, where the symmetries of the space were transformations forming a Lie group. The geometries of interest were homogeneous space
s G/H, but usually without a fixed choice of origin corresponding to the coset
eH.
A principal homogeneous space of G is a manifold P abstractly characterized by having a free and transitive action
of G on P. The Maurer–Cartan form gives an appropriate infinitesimal characterization of the principal homogeneous space. It is a one-form defined on P satisfying an integrability condition known as the Maurer–Cartan equation. Using this integrability condition, it is possible to define the exponential map
of the Lie algebra and in this way obtain, locally, a group action on P.
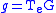be the tangent space of a Lie group 
at the identity (its Lie algebra
).
acts on itself by left translation
such that for a given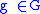
we have
and this induces a map of the tangent bundle
to itself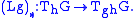
A left-invariant vector field
is a section
of 
such that
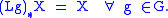
The Maurer–Cartan form
is a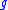 
-valued one-form on 
defined on vectors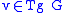 
by the formula
is embedded in 
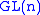by a matrix valued mapping 
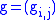, then one can write 
explicitly as
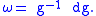
In this sense, the Maurer–Cartan form is always the left logarithmic derivative
of the identity map of
.
. It is the unique g = TeG valued 1-form on G satisfying
where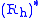
is the pullback of forms along the right-translation in the group and Ad(h−1) is the adjoint action on the Lie algebra.
is a left-invariant vector field on 
, then 
is constant on 
. Furthermore, if 
and 
are both left-invariant, then
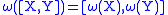
where the bracket on the left-hand side is the Lie bracket of vector fields
, and the bracket on the right-hand side is the bracket on the Lie algebra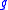
. (This may be used as the definition of the bracket on 
.) These facts may be used to establish an isomorphism of Lie algebras
By the definition of the exterior derivative
, if
and 
are arbitrary vector fields then
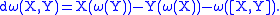
Here ω(Y) is the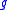
-valued function obtained by duality from pairing the one-form ω with the vector field Y, and X(ω(Y)) is the Lie derivative
of this function along X. Similarly Y(ω(X)) is the Lie derivative along Y of the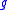
-valued function ω(X).
In particular, if
and 
are left-invariant, then
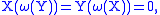
so
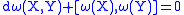
but the left-hand side is simply a 2-form, so the equation does not rely on the fact that
and 
are left-invariant. The conclusion follows that the equation is true for any pair of vector fields 
and 
. This is known as the Maurer–Cartan equation. It is often written as
Since Ei is left-invariant, applying the Maurer–Cartan form to it simply returns the value of Ei at the identity. Thus ω(Ei) = Ei(e) ∈ g. Thus, the Maurer–Cartan form can be written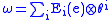
(1).
Suppose that the Lie brackets of the vector fields Ei are given by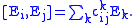
The quantities cijk are constant, and called the structure constants of the Lie algebra (relative to the basis Ei). A simple calculation, using the definition of the exterior derivative d, yields
so that by duality
(2).
This equation is also often called the Maurer–Cartan equation. To relate it to the previous definition, which only involved the Maurer–Cartan form ω, take the exterior derivative of (1):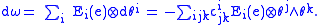
The frame components are given by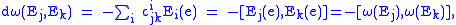
which establishes the equivalence of the two forms of the Maurer–Cartan equation.
associated to a homogeneous space
. If H is a closed subgroup of G, then G/H is a smooth manifold of dimension dim G - dim H. The quotient map G → G/H induces the structure of an H-principal bundle over G/H. The Maurer–Cartan form on the Lie group G yields a flat Cartan connection
for this principal bundle. In particular, if H = {e}, then this Cartan connection is an ordinary connection form
, and we have
which is the condition for the vanishing of the curvature.
In the method of moving frames, one sometimes considers a local section of the tautological bundle, say s : G/H → G. (If working on a submanifold
of the homogeneous space, then s need only be a local section over the submanifold.) The pullback of the Maurer–Cartan form along s defines a non-degenerate g-valued 1-form θ = s*ω over the base. The Maurer–Cartan equation implies that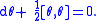
Morever, if sU and sV are a pair of local sections defined, respectively, over open sets U and V, then they are related by an element of H in each fibre of the bundle:
The differential of h gives a compatibility condition relating the two sections on the overlap region: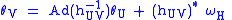
where ωH is the Maurer–Cartan form on the group H.
A system of non-degenerate g-valued 1-forms θU defined on open sets in a manifold M, satisfying the Maurer–Cartan structural equations and the compatibility conditions endows the manifold M locally with the structure of the homogeneous space G/H. In other words, there is locally a diffeomorphism
of M into the homogeneous space, such that θU is the pullback of the Maurer–Cartan form along some section of the tautological bundle. This is a consequence of the existence of primitives of the Darboux derivative
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Maurer–Cartan form for a Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
G is a distinguished differential one-form
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
on G that carries the basic infinitesimal information about the structure of G. It was much used by Élie Cartan
Élie Cartan
Élie Joseph Cartan was an influential French mathematician, who did fundamental work in the theory of Lie groups and their geometric applications...
as a basic ingredient of his method of moving frames, and bears his name together with that of Ludwig Maurer
Ludwig Maurer
Ludwig Maurer was a German mathematician professor on the Tübingen University. He was the eldest son of Konrad von Maurer and Valerie von Faulhaber . His 1887 dissertation at the University of Strassburg was on the theory of linear substitutions, known today as matrix groups...
.
As a one-form, the Maurer–Cartan form is peculiar in that it takes its values in the Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
associated to the Lie group G. The Lie algebra is identified with the tangent space
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
of G at the identity, denoted TeG. The Maurer–Cartan form ω is thus a one-form defined globally on G which is a linear mapping of the tangent space TgG at each g ∈ G into TeG. It is given as the pushforward of a vector in TgG along the left-translation in the group:
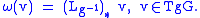
Motivation and interpretation
A Lie group acts on itself by multiplication under the mapping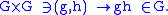A question of importance to Cartan and his contemporaries was how to identify a principal homogeneous space
Principal homogeneous space
In mathematics, a principal homogeneous space, or torsor, for a group G is a homogeneous space X for G such that the stabilizer subgroup of any point is trivial...
of G. That is, a manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
P identical to the group G, but without a fixed choice of unit element. This motivation came, in part, from Felix Klein
Felix Klein
Christian Felix Klein was a German mathematician, known for his work in group theory, function theory, non-Euclidean geometry, and on the connections between geometry and group theory...
's Erlangen programme where one was interested in a notion of symmetry
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
on a space, where the symmetries of the space were transformations forming a Lie group. The geometries of interest were homogeneous space
Homogeneous space
In mathematics, particularly in the theories of Lie groups, algebraic groups and topological groups, a homogeneous space for a group G is a non-empty manifold or topological space X on which G acts continuously by symmetry in a transitive way. A special case of this is when the topological group,...
s G/H, but usually without a fixed choice of origin corresponding to the coset
Coset
In mathematics, if G is a group, and H is a subgroup of G, and g is an element of G, thenA coset is a left or right coset of some subgroup in G...
eH.
A principal homogeneous space of G is a manifold P abstractly characterized by having a free and transitive action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
of G on P. The Maurer–Cartan form gives an appropriate infinitesimal characterization of the principal homogeneous space. It is a one-form defined on P satisfying an integrability condition known as the Maurer–Cartan equation. Using this integrability condition, it is possible to define the exponential map
Exponential map
In differential geometry, the exponential map is a generalization of the ordinary exponential function of mathematical analysis to all differentiable manifolds with an affine connection....
of the Lie algebra and in this way obtain, locally, a group action on P.
Intrinsic construction
Let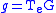 be the tangent space of a Lie group at the identity (its Lie algebraLie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
).
acts on itself by left translationsuch that for a given
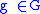we haveand this induces a map of the tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
to itself
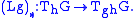
A left-invariant vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
is a section
of such that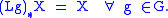The Maurer–Cartan form
is a 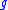-valued one-form on defined on vectors 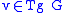by the formula
Extrinsic construction
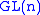If is embedded in by a matrix valued mapping 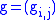, then one can write explicitly as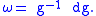In this sense, the Maurer–Cartan form is always the left logarithmic derivative
Logarithmic derivative
In mathematics, specifically in calculus and complex analysis, the logarithmic derivative of a function f is defined by the formulawhere f ′ is the derivative of f....
of the identity map of
.Characterization as a connection
The Maurer–-Cartan form can also be characterized abstractly as a kind of principal connectionConnection (principal bundle)
In mathematics, a connection is a device that defines a notion of parallel transport on the bundle; that is, a way to "connect" or identify fibers over nearby points...
. It is the unique g = TeG valued 1-form on G satisfying
where
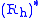is the pullback of forms along the right-translation in the group and Ad(h−1) is the adjoint action on the Lie algebra.Properties
If is a left-invariant vector field on , then is constant on . Furthermore, if and are both left-invariant, then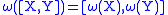where the bracket on the left-hand side is the Lie bracket of vector fields
Lie bracket of vector fields
In the mathematical field of differential topology, the Lie bracket of vector fields, Jacobi–Lie bracket, or commutator of vector fields is a bilinear differential operator which assigns, to any two vector fields X and Y on a smooth manifold M, a third vector field denoted [X, Y]...
, and the bracket on the right-hand side is the bracket on the Lie algebra
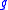. (This may be used as the definition of the bracket on .) These facts may be used to establish an isomorphism of Lie algebrasBy the definition of the exterior derivative
Exterior derivative
In differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
, if
and are arbitrary vector fields then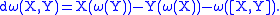Here ω(Y) is the
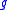-valued function obtained by duality from pairing the one-form ω with the vector field Y, and X(ω(Y)) is the Lie derivativeLie derivative
In mathematics, the Lie derivative , named after Sophus Lie by Władysław Ślebodziński, evaluates the change of a vector field or more generally a tensor field, along the flow of another vector field...
of this function along X. Similarly Y(ω(X)) is the Lie derivative along Y of the
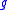-valued function ω(X).In particular, if
and are left-invariant, then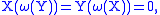so
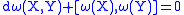
but the left-hand side is simply a 2-form, so the equation does not rely on the fact that
and are left-invariant. The conclusion follows that the equation is true for any pair of vector fields and . This is known as the Maurer–Cartan equation. It is often written asMaurer–Cartan frame
One can also view the Maurer–Cartan form as being constructed from a Maurer–Cartan frame. Let Ei be a basis of sections of TG consisting of left-invariant vector fields, and θj be the dual basis of sections of T*G such that θj(Ei) = δij, the Kronecker delta. Then Ei is a Maurer–Cartan frame, and θi is a Maurer–Cartan coframe.Since Ei is left-invariant, applying the Maurer–Cartan form to it simply returns the value of Ei at the identity. Thus ω(Ei) = Ei(e) ∈ g. Thus, the Maurer–Cartan form can be written
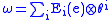(1).Suppose that the Lie brackets of the vector fields Ei are given by
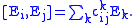
The quantities cijk are constant, and called the structure constants of the Lie algebra (relative to the basis Ei). A simple calculation, using the definition of the exterior derivative d, yields
so that by duality
(2).This equation is also often called the Maurer–Cartan equation. To relate it to the previous definition, which only involved the Maurer–Cartan form ω, take the exterior derivative of (1):
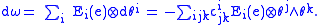
The frame components are given by
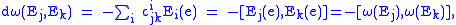
which establishes the equivalence of the two forms of the Maurer–Cartan equation.
Maurer–Cartan form on a homogeneous space
Maurer–Cartan forms play an important role in Cartan's method of moving frames. In this context, one may view the Maurer–Cartan form as a 1-form defined on the tautological principal bundlePrincipal bundle
In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
associated to a homogeneous space
Homogeneous space
In mathematics, particularly in the theories of Lie groups, algebraic groups and topological groups, a homogeneous space for a group G is a non-empty manifold or topological space X on which G acts continuously by symmetry in a transitive way. A special case of this is when the topological group,...
. If H is a closed subgroup of G, then G/H is a smooth manifold of dimension dim G - dim H. The quotient map G → G/H induces the structure of an H-principal bundle over G/H. The Maurer–Cartan form on the Lie group G yields a flat Cartan connection
Cartan connection
In the mathematical field of differential geometry, a Cartan connection is a flexible generalization of the notion of an affine connection. It may also be regarded as a specialization of the general concept of a principal connection, in which the geometry of the principal bundle is tied to the...
for this principal bundle. In particular, if H = {e}, then this Cartan connection is an ordinary connection form
Connection form
In mathematics, and specifically differential geometry, a connection form is a manner of organizing the data of a connection using the language of moving frames and differential forms....
, and we have
which is the condition for the vanishing of the curvature.
In the method of moving frames, one sometimes considers a local section of the tautological bundle, say s : G/H → G. (If working on a submanifold
Submanifold
In mathematics, a submanifold of a manifold M is a subset S which itself has the structure of a manifold, and for which the inclusion map S → M satisfies certain properties. There are different types of submanifolds depending on exactly which properties are required...
of the homogeneous space, then s need only be a local section over the submanifold.) The pullback of the Maurer–Cartan form along s defines a non-degenerate g-valued 1-form θ = s*ω over the base. The Maurer–Cartan equation implies that
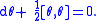
Morever, if sU and sV are a pair of local sections defined, respectively, over open sets U and V, then they are related by an element of H in each fibre of the bundle:
The differential of h gives a compatibility condition relating the two sections on the overlap region:
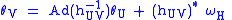
where ωH is the Maurer–Cartan form on the group H.
A system of non-degenerate g-valued 1-forms θU defined on open sets in a manifold M, satisfying the Maurer–Cartan structural equations and the compatibility conditions endows the manifold M locally with the structure of the homogeneous space G/H. In other words, there is locally a diffeomorphism
Diffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
of M into the homogeneous space, such that θU is the pullback of the Maurer–Cartan form along some section of the tautological bundle. This is a consequence of the existence of primitives of the Darboux derivative
Darboux derivative
The Darboux derivative of a map between a manifold and a Lie group is a variant of the standard derivative. In a certain sense, it is arguably a more natural generalization of the single-variable derivative...
.