
Congruence (geometry)
Encyclopedia
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, two figures are congruent if they have the same shape
Shape
The shape of an object located in some space is a geometrical description of the part of that space occupied by the object, as determined by its external boundary – abstracting from location and orientation in space, size, and other properties such as colour, content, and material...
and size. This means that either object can be repositioned so as to coincide precisely with the other object. More formally, two sets of points
Point (geometry)
In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
are called congruent if, and only if, one can be transformed into the other by an isometry
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
, i.e., a combination of translation
Translation (geometry)
In Euclidean geometry, a translation moves every point a constant distance in a specified direction. A translation can be described as a rigid motion, other rigid motions include rotations and reflections. A translation can also be interpreted as the addition of a constant vector to every point, or...
s, rotation
Rotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
s and reflection
Reflection (mathematics)
In mathematics, a reflection is a mapping from a Euclidean space to itself that is an isometry with a hyperplane as set of fixed points; this set is called the axis or plane of reflection. The image of a figure by a reflection is its mirror image in the axis or plane of reflection...
s.
The related concept of similarity
Similarity (geometry)
Two geometrical objects are called similar if they both have the same shape. More precisely, either one is congruent to the result of a uniform scaling of the other...
applies if the objects differ in size but not in shape.
Definition of congruence in analytic geometry
In a Euclidean systemEuclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
, congruence is fundamental; it is the counterpart of equality for numbers. In analytic geometry
Analytic geometry
Analytic geometry, or analytical geometry has two different meanings in mathematics. The modern and advanced meaning refers to the geometry of analytic varieties...
, congruence may be defined intuitively thus: two mappings of figures onto one Cartesian coordinate system are congruent if and only if, for any two points in the first mapping, the Euclidean distance
Euclidean distance
In mathematics, the Euclidean distance or Euclidean metric is the "ordinary" distance between two points that one would measure with a ruler, and is given by the Pythagorean formula. By using this formula as distance, Euclidean space becomes a metric space...
between them is equal to the Euclidean distance between the corresponding points in the second mapping.
A more formal definition: two subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
s A and B of Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rn are called congruent if there exists an isometry
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
f : Rn → Rn (an element of the Euclidean group
Euclidean group
In mathematics, the Euclidean group E, sometimes called ISO or similar, is the symmetry group of n-dimensional Euclidean space...
E(n)) with f(A) = B. Congruence is an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
.
Congruence of triangles
- See also Solution of trianglesSolution of trianglesIn trigonometry, to solve a triangle is to find the three angles and the lengths of the three sides of the triangle when given some, but not all of that information...
.
Two triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
s are congruent if their corresponding side
Side
Side was an ancient Greek city in Anatolia, in the region of Pamphylia, in what is now Antalya province, on the southern Mediterranean coast of Turkey...
s are equal in length and their corresponding angle
Angle
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
s are equal in size.
If triangle ABC is congruent to triangle DEF, the relationship can be written mathematically as:

In many cases it is sufficient to establish the equality of three corresponding parts and use one of the following results to deduce the congruence of the two triangles.
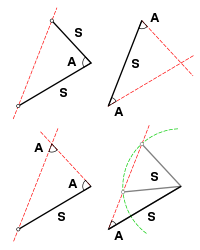
Determining congruence
Sufficient evidence for congruence between two triangles in Euclidean spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
can be shown through the following comparisons:
- SAS (Side-Angle-Side): If two pairs of sides of two triangles are equal in length, and the included angleIncluded angleThe concept of included angle is discussed at:* Congruence of triangles* Solution of triangles...
s are equal in measurement, then the triangles are congruent. - SSS (Side-Side-Side): If three pairs of sides of two triangles are equal in length, then the triangles are congruent.
- ASA (Angle-Side-Angle): If two pairs of angles of two triangles are equal in measurement, and the included sides are equal in length, then the triangles are congruent.
The ASA Postulate was contributed by Thales of Miletus (Greek). In most systems of axioms, the three criteria—SAS, SSS and ASA—are established as theoremTheoremIn mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
s. In the School Mathematics Study GroupSchool Mathematics Study GroupThe School Mathematics Study Group was an American academic think tank focused on the subject of reform in mathematics education. Directed by Edward G...
system SAS is taken as one (#15) of 22 postulates. - AAS (Angle-Angle-Side): If two pairs of angles of two triangles are equal in measurement, and a pair of corresponding non-included sides are equal in length, then the triangles are congruent. (In British usage, ASA and AAS are usually combined into a single condition AAcorrS - any two angles and a corresponding side.)
- RHS (Right-angle-Hypotenuse-Side): If two right-angled triangles have their hypotenuses equal in length, and a pair of shorter sides are equal in length, then the triangles are congruent.
Side-Side-Angle
The SSA condition (Side-Side-Angle) which specifies two sides and a non-included angle (also known as ASS, or Angle-Side-Side) does not by itself prove congruence. In order to show congruence, additional information is required such as the measure of the corresponding angles and in some cases the lengths of the two pairs of corresponding sides. There are four possible cases:If two triangles satisfy the SSA condition and the corresponding angles are either obtuse or right, then the two triangles are congruent. In this situation, the length of the side opposite the angle will be greater than the length of the adjacent side. Where the angle is a right angle, also known as the Hypotenuse-Leg (HL) postulate or the Right-angle-Hypotenuse-Side (RHS) condition, the third side can be calculated using the Pythagoras' Theorem thus allowing the SSS postulate to be applied.
If two triangles satisfy the SSA condition and the corresponding angles are acute and the length of the side opposite the angle is greater than or equal to the length of the adjacent side, then the two triangles are congruent.
If two triangles satisfy the SSA condition and the corresponding angles are acute and the length of the side opposite the angle is equal to the length of the adjacent side multiplied by the sine of the angle, then the two triangles are congruent.
If two triangles satisfy the SSA condition and the corresponding angles are acute and the length of the side opposite the angle is greater than the length of the adjacent side multiplied by the sine of the angle (but less than the length of the adjacent side), then the two triangles cannot be shown to be congruent. This is the ambiguous case and two different triangles can be formed from the given information.
Angle-Angle-Angle
In Euclidean geometry, AAA (Angle-Angle-Angle) (or just AA, since in Euclidean geometry the angles of a triangle add up to 180°) does not provide information regarding the size of the two triangles and hence proves only similaritySimilarity (geometry)
Two geometrical objects are called similar if they both have the same shape. More precisely, either one is congruent to the result of a uniform scaling of the other...
and not congruence in Euclidean space.
However, in spherical geometry
Spherical geometry
Spherical geometry is the geometry of the two-dimensional surface of a sphere. It is an example of a geometry which is not Euclidean. Two practical applications of the principles of spherical geometry are to navigation and astronomy....
and hyperbolic geometry
Hyperbolic geometry
In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
(where the sum of the angles of a triangle varies with size) AAA is sufficient for congruence on a given curvature of surface.
External links
- The SSS at Cut-the-KnotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
- The SSA at Cut-the-KnotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
- Interactive animations demonstrating Congruent angles, Congruent line segments, Congruent triangles, Congruent polygons

