
First Hurwitz triplet
Encyclopedia
In the mathematical theory of Riemann surface
s, the first Hurwitz triplet is a triple of distinct Hurwitz surface
s with the identical automorphism group of the lowest possible genus, namely 14 (genera 3 and 7 admit a unique Hurwitz surface, respectively the Klein quartic
and the Macbeath surface
). The explanation for this phenomenon is arithmetic. Namely, in the ring of integers of the appropriate number field, the rational prime 13 splits as a product of three distinct prime ideals. The principal congruence subgroup
s defined by the triplet of primes produce Fuchsian group
s corresponding to the triplet of Riemann surfaces.
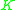 be the real subfield of
be the real subfield of 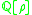 where
where 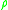 is a 7th-primitive root of unity
is a 7th-primitive root of unity
.
The ring of integers
of K is , where
, where 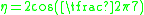 . Let
. Let 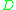 be the quaternion algebra
be the quaternion algebra
, or symbol algebra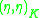 . Also Let
. Also Let 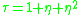 and
and 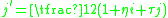 . Let
. Let  . Then
. Then 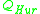 is a maximal order of
is a maximal order of 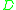 (see Hurwitz quaternion order
(see Hurwitz quaternion order
), described explicitly by Noam Elkies
[1].
In order to construct the first Hurwitz triplet, consider the prime decomposition of 13 in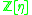 , namely
, namely
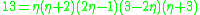 ,
,
where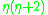 is invertible. Also consider the prime ideals generated by the non-invertible factors. The principal congruence subgroup defined by such a prime ideal I is by definition the group
is invertible. Also consider the prime ideals generated by the non-invertible factors. The principal congruence subgroup defined by such a prime ideal I is by definition the group
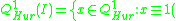 mod
mod 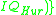 ,
,
namely, the group of elements of reduced norm 1 in equivalent to 1 modulo the ideal
equivalent to 1 modulo the ideal 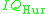 . The corresponding Fuchsian group is obtained as the image of the principal congruence subgroup under a representation to PSL(2,R).
. The corresponding Fuchsian group is obtained as the image of the principal congruence subgroup under a representation to PSL(2,R).
Each of the three Riemann surfaces in the first Hurwitz triplet can be formed as a Fuchsian model
, the quotient of the hyperbolic plane
by one of these three Fuchsian groups.
states that
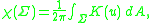
where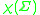 is the Euler characteristic
is the Euler characteristic
of the surface and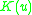 is the Gaussian curvature
is the Gaussian curvature
. In the case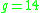 we have
we have
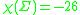 and
and 
thus we obtain that the area of these surfaces is
 .
.
The lower bound on the systole as specified in [2], namely
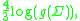
is 3.5187.
Some specific details about each of the surfaces are presented in the following tables (the number of systolic loops is taken from [3]).The term Systolic Trace refers to the least reduced trace of an element in the corresponding subgroup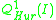 . The systolic ratio is the ratio of the square of the systole to the area.
. The systolic ratio is the ratio of the square of the systole to the area.
Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
s, the first Hurwitz triplet is a triple of distinct Hurwitz surface
Hurwitz surface
In Riemann surface theory and hyperbolic geometry, a Hurwitz surface, named after Adolf Hurwitz, is a compact Riemann surface with preciselyautomorphisms, where g is the genus of the surface. This number is maximal by virtue of Hurwitz's theorem on automorphisms...
s with the identical automorphism group of the lowest possible genus, namely 14 (genera 3 and 7 admit a unique Hurwitz surface, respectively the Klein quartic
Klein quartic
In hyperbolic geometry, the Klein quartic, named after Felix Klein, is a compact Riemann surface of genus 3 with the highest possible order automorphism group for this genus, namely order 168 orientation-preserving automorphisms, and 336 automorphisms if orientation may be reversed...
and the Macbeath surface
Macbeath surface
In Riemann surface theory and hyperbolic geometry, the Macbeath surface, also called Macbeath's curve or the Fricke–Macbeath curve, is the genus-7 Hurwitz surface....
). The explanation for this phenomenon is arithmetic. Namely, in the ring of integers of the appropriate number field, the rational prime 13 splits as a product of three distinct prime ideals. The principal congruence subgroup
Congruence subgroup
In mathematics, a congruence subgroup of a matrix group with integer entries is a subgroup defined by congruence conditions on the entries. A very simple example would be invertible 2x2 integer matrices of determinant 1, such that the off-diagonal entries are even.An importance class of congruence...
s defined by the triplet of primes produce Fuchsian group
Fuchsian group
In mathematics, a Fuchsian group is a discrete subgroup of PSL. The group PSL can be regarded as a group of isometries of the hyperbolic plane, or conformal transformations of the unit disc, or conformal transformations of the upper half plane, so a Fuchsian group can be regarded as a group acting...
s corresponding to the triplet of Riemann surfaces.
Arithmetic construction
Let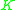 be the real subfield of
be the real subfield of 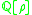 where
where 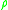 is a 7th-primitive root of unity
is a 7th-primitive root of unityRoot of unity
In mathematics, a root of unity, or de Moivre number, is any complex number that equals 1 when raised to some integer power n. Roots of unity are used in many branches of mathematics, and are especially important in number theory, the theory of group characters, field theory, and the discrete...
.
The ring of integers
Ring of integers
In mathematics, the ring of integers is the set of integers making an algebraic structure Z with the operations of integer addition, negation, and multiplication...
of K is
 , where
, where 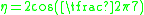 . Let
. Let 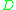 be the quaternion algebra
be the quaternion algebraQuaternion algebra
In mathematics, a quaternion algebra over a field F is a central simple algebra A over F that has dimension 4 over F. Every quaternion algebra becomes the matrix algebra by extending scalars , i.e...
, or symbol algebra
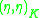 . Also Let
. Also Let 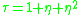 and
and 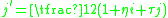 . Let
. Let  . Then
. Then 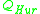 is a maximal order of
is a maximal order of 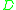 (see Hurwitz quaternion order
(see Hurwitz quaternion orderHurwitz quaternion order
The Hurwitz quaternion order is a specific order in a quaternion algebra over a suitable number field. The order is of particular importance in Riemann surface theory, in connection with surfaces with maximal symmetry, namely the Hurwitz surfaces. The Hurwitz quaternion order was studied in 1967...
), described explicitly by Noam Elkies
Noam Elkies
Noam David Elkies is an American mathematician and chess master.At age 14, Elkies received a gold medal with a perfect score at the International Mathematical Olympiad, the youngest ever to do so...
[1].
In order to construct the first Hurwitz triplet, consider the prime decomposition of 13 in
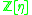 , namely
, namely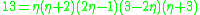 ,
,where
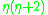 is invertible. Also consider the prime ideals generated by the non-invertible factors. The principal congruence subgroup defined by such a prime ideal I is by definition the group
is invertible. Also consider the prime ideals generated by the non-invertible factors. The principal congruence subgroup defined by such a prime ideal I is by definition the group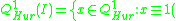 mod
mod 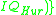 ,
,namely, the group of elements of reduced norm 1 in
 equivalent to 1 modulo the ideal
equivalent to 1 modulo the ideal 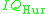 . The corresponding Fuchsian group is obtained as the image of the principal congruence subgroup under a representation to PSL(2,R).
. The corresponding Fuchsian group is obtained as the image of the principal congruence subgroup under a representation to PSL(2,R).Each of the three Riemann surfaces in the first Hurwitz triplet can be formed as a Fuchsian model
Fuchsian model
In mathematics, a Fuchsian model is a construction of a hyperbolic Riemann surface R as a quotient of the upper half-plane H. By the uniformization theorem, every Riemann surface is either elliptic, parabolic or hyperbolic. Every hyperbolic Riemann surface has a non-trivial fundamental group \pi_1...
, the quotient of the hyperbolic plane
Hyperbolic manifold
In mathematics, a hyperbolic n-manifold is a complete Riemannian n-manifold of constant sectional curvature -1.Every complete, connected, simply-connected manifold of constant negative curvature −1 is isometric to the real hyperbolic space Hn. As a result, the universal cover of any closed manifold...
by one of these three Fuchsian groups.
Bound for systolic length and the systolic ratio
The Gauss–Bonnet theoremGauss–Bonnet theorem
The Gauss–Bonnet theorem or Gauss–Bonnet formula in differential geometry is an important statement about surfaces which connects their geometry to their topology...
states that
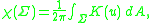
where
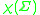 is the Euler characteristic
is the Euler characteristicEuler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
of the surface and
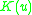 is the Gaussian curvature
is the Gaussian curvatureGaussian curvature
In differential geometry, the Gaussian curvature or Gauss curvature of a point on a surface is the product of the principal curvatures, κ1 and κ2, of the given point. It is an intrinsic measure of curvature, i.e., its value depends only on how distances are measured on the surface, not on the way...
. In the case
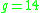 we have
we have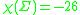 and
and 
thus we obtain that the area of these surfaces is
 .
.The lower bound on the systole as specified in [2], namely
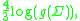
is 3.5187.
Some specific details about each of the surfaces are presented in the following tables (the number of systolic loops is taken from [3]).The term Systolic Trace refers to the least reduced trace of an element in the corresponding subgroup
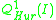 . The systolic ratio is the ratio of the square of the systole to the area.
. The systolic ratio is the ratio of the square of the systole to the area.
| Ideal | 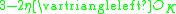 |
| Systole | 5.9039 |
| Systolic Trace | 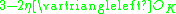 |
| Systolic Ratio | 0.2133 |
| Number of Systolic Loops |
| Ideal | 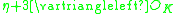 |
| Systole | 6.3933 |
| Systolic Trace | 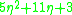 |
| Systolic Ratio | 0.2502 |
| Number of Systolic Loops |
| Ideal | 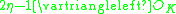 |
| Systole | 6.8879 |
| Systolic Trace |  |
| Systolic Ratio | 0.2904 |
| Number of Systolic Loops |

