
Smooth structure
Encyclopedia
In mathematics
, a smooth structure on a manifold
allows for an unambiguous notion of smooth function
. In particular, a smooth structure allows one to perform mathematical analysis
on the manifold.
A smooth structure on a manifold M is a collection of smoothly equivalent smooth atlases. Here, a smooth atlas for a topological manifold M is an atlas
for M such that each transition function
is a smooth map, and two smooth atlases for M are smoothly equivalent provided their union
is again a smooth atlas for M. This gives a natural equivalence relation
on the set of smooth atlases.
showed in 1956 that the 7-dimensional sphere admits a smooth structure that is distinct from the standard smooth structure. A sphere equipped with a nonstandard smooth structure is called an exotic sphere
.
Thus, we may regard a smooth structure as a maximal atlas and vice versa.
In general, computations with the maximal atlas of a manifold are rather unwieldy. For most applications, it suffices to choose a smaller atlas.
For example, if the manifold is compact
, then one can find an atlas with only finitely many charts.
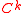 or (real-)analytic structure
or (real-)analytic structure
on the manifold rather than a smooth one. Similarly, we can define a complex structure
by requiring the transition maps to be holomorphic.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a smooth structure on a manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
allows for an unambiguous notion of smooth function
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
. In particular, a smooth structure allows one to perform mathematical analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
on the manifold.
A smooth structure on a manifold M is a collection of smoothly equivalent smooth atlases. Here, a smooth atlas for a topological manifold M is an atlas
Atlas (topology)
In mathematics, particularly topology, one describesa manifold using an atlas. An atlas consists of individualcharts that, roughly speaking, describe individual regionsof the manifold. If the manifold is the surface of the Earth,...
for M such that each transition function
Transition function
In mathematics, a transition function has several different meanings:* In topology, a transition function is a homeomorphism from one coordinate chart to another...
is a smooth map, and two smooth atlases for M are smoothly equivalent provided their union
Union (set theory)
In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
is again a smooth atlas for M. This gives a natural equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
on the set of smooth atlases.
Exotic spheres
John MilnorJohn Milnor
John Willard Milnor is an American mathematician known for his work in differential topology, K-theory and dynamical systems. He won the Fields Medal in 1962, the Wolf Prize in 1989, and the Abel Prize in 2011. Milnor is a distinguished professor at Stony Brook University...
showed in 1956 that the 7-dimensional sphere admits a smooth structure that is distinct from the standard smooth structure. A sphere equipped with a nonstandard smooth structure is called an exotic sphere
Exotic sphere
In differential topology, a mathematical discipline, an exotic sphere is a differentiable manifold M that is homeomorphic but not diffeomorphic to the standard Euclidean n-sphere...
.
Maximal smooth atlases
By taking the union of all atlases belonging to a smooth structure, we obtain a maximal smooth atlas. This atlas contains every chart that is compatible with the smooth structure. There is a natural one to one correspondence between smooth structures and maximal smooth atlases.Thus, we may regard a smooth structure as a maximal atlas and vice versa.
In general, computations with the maximal atlas of a manifold are rather unwieldy. For most applications, it suffices to choose a smaller atlas.
For example, if the manifold is compact
Compact
Compact as used in politics may refer broadly to a pact or treaty; in more specific cases it may refer to:* Interstate compact* Compact government, a type of colonial rule utilized in British North America...
, then one can find an atlas with only finitely many charts.
Related structures
The smoothness requirements on the transition functions can be weakened, so that we only require the transition maps to be k-times continuously differentiable; or strengthened, so that we require the transition maps to real-analytic. Accordingly, this gives a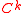 or (real-)analytic structure
or (real-)analytic structureAnalytic manifold
In mathematics, an analytic manifold is a topological manifold with analytic transition maps. Every complex manifold is an analytic manifold....
on the manifold rather than a smooth one. Similarly, we can define a complex structure
Complex manifold
In differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....
by requiring the transition maps to be holomorphic.

