
Quasiconformal mapping
Encyclopedia
In mathematical complex analysis
, a quasiconformal mapping, introduced by and named by , is a homeomorphism between plane domains which to first order takes small circles to small ellipses of bounded eccentricity.
Intuitively, let ƒ:D → D′ be an orientation
-preserving homeomorphism
between open set
s in the plane. If f is continuously differentiable, then it is K-quasiconformal if the derivative of at every point maps circles to ellipses with eccentricity bounded by K.
at every point maps circles to ellipses with eccentricity bounded by K.
partial derivative
s, then ƒ is quasiconformal provided it satisfies the Beltrami equation
for some complex valued Lebesgue measurable μ satisfying sup |μ| < 1 . This equation admits a geometrical interpretation. Equip D with the metric tensor
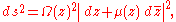
where Ω(z) > 0. Then ƒ satisfies precisely when it is a conformal transformation from D equipped with this metric to the domain D′ equipped with the standard Euclidean metric. The function ƒ is then called μ-conformal. More generally, the continuous differentiability of ƒ can be replaced by the weaker condition that ƒ be in the Sobolev space
W1,2(D) of functions whose first-order distributional derivatives are in L2(D)
. In this case, ƒ is required to be a weak solution
of . When μ is zero almost everywhere, any homeomorphism in W1,2(D) that is a weak solution of is conformal.
Without appeal to an auxiliary metric, consider the effect of the pullback under ƒ of the usual Euclidean metric. The resulting metric is then given by

which, relative to the background Euclidean metric , has eigenvalues
, has eigenvalues
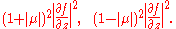
The eigenvalues represent, respectively, the squared length of the major and minor axis of the ellipse obtained by pulling back along f the unit circle in the tangent plane.
Accordingly, the dilatation of ƒ at a point z is defined by
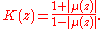
The (essential) supremum
of K(z) is given by

and is called the dilatation of ƒ.
A definition based on the notion of extremal length
is as follows. If there is a finite K such that for every collection Γ of curves in D the extremal length of Γ is at most K times the extremal length of { ƒ o γ : γ ∈ Γ }. Then ƒ is K-quasiconformal.
If ƒ is K-quasiconformal for some finite K, then ƒ is quasiconformal.
The map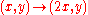 is 2-quasiconformal.
is 2-quasiconformal.
The map is quasiconformal if
is quasiconformal if  (here
(here  is a complex number). This is an example of a quasiconformal homeomorphism that is not smooth. If
is a complex number). This is an example of a quasiconformal homeomorphism that is not smooth. If  , this is simply the identity map.
, this is simply the identity map.
If is
is  quasiconformal and
quasiconformal and 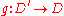 is
is 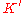 quasiconformal, then
quasiconformal, then  is
is 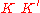 quasiconformal.
quasiconformal.
The inverse of a K-quasiconformal homeomorphism is K-quasiconformal.
The space of K-quasiconformal mappings from the complex plane to itself mapping three distinct points to three given points is compact.
, proved by . The theorem generalizes the Riemann mapping theorem from conformal to quasiconformal homeomorphisms, and is stated as follows. Suppose that D is a simply connected domain in C that is not equal to C, and suppose that is Lebesgue measurable and satisfies
is Lebesgue measurable and satisfies  . Then there is a quasiconformal homeomorphism ƒ from D to the unit disk which is in the Sobolev space W1,2(D) and satisfies the corresponding Beltrami equation in the distributional sense
. Then there is a quasiconformal homeomorphism ƒ from D to the unit disk which is in the Sobolev space W1,2(D) and satisfies the corresponding Beltrami equation in the distributional sense
. As with Riemann's mapping theorem, this ƒ is unique up to 3 real parameters.
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
, a quasiconformal mapping, introduced by and named by , is a homeomorphism between plane domains which to first order takes small circles to small ellipses of bounded eccentricity.
Intuitively, let ƒ:D → D′ be an orientation
Orientation (mathematics)
In mathematics, orientation is a notion that in two dimensions allows one to say when a cycle goes around clockwise or counterclockwise, and in three dimensions when a figure is left-handed or right-handed. In linear algebra, the notion of orientation makes sense in arbitrary dimensions...
-preserving homeomorphism
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
between open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
s in the plane. If f is continuously differentiable, then it is K-quasiconformal if the derivative of
 at every point maps circles to ellipses with eccentricity bounded by K.
at every point maps circles to ellipses with eccentricity bounded by K.Definition
Suppose ƒ:D → D′ where D and D′ are two domains in C. There are a variety of equivalent definitions, depending on the required smoothness of ƒ. If ƒ is assumed to have continuousContinuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
partial derivative
Partial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
s, then ƒ is quasiconformal provided it satisfies the Beltrami equation
for some complex valued Lebesgue measurable μ satisfying sup |μ| < 1 . This equation admits a geometrical interpretation. Equip D with the metric tensor
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
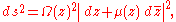
where Ω(z) > 0. Then ƒ satisfies precisely when it is a conformal transformation from D equipped with this metric to the domain D′ equipped with the standard Euclidean metric. The function ƒ is then called μ-conformal. More generally, the continuous differentiability of ƒ can be replaced by the weaker condition that ƒ be in the Sobolev space
Sobolev space
In mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...
W1,2(D) of functions whose first-order distributional derivatives are in L2(D)
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
. In this case, ƒ is required to be a weak solution
Weak solution
In mathematics, a weak solution to an ordinary or partial differential equation is a function for which the derivatives may not all exist but which is nonetheless deemed to satisfy the equation in some precisely defined sense. There are many different definitions of weak solution, appropriate for...
of . When μ is zero almost everywhere, any homeomorphism in W1,2(D) that is a weak solution of is conformal.
Without appeal to an auxiliary metric, consider the effect of the pullback under ƒ of the usual Euclidean metric. The resulting metric is then given by

which, relative to the background Euclidean metric
 , has eigenvalues
, has eigenvalues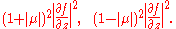
The eigenvalues represent, respectively, the squared length of the major and minor axis of the ellipse obtained by pulling back along f the unit circle in the tangent plane.
Accordingly, the dilatation of ƒ at a point z is defined by
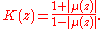
The (essential) supremum
Supremum
In mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
of K(z) is given by

and is called the dilatation of ƒ.
A definition based on the notion of extremal length
Extremal length
In the mathematical theory of conformal and quasiconformal mappings, the extremal length of a collection of curves \Gamma is a conformal invariant of \Gamma. More specifically, suppose thatD is an open set in the complex plane and \Gamma is a collection...
is as follows. If there is a finite K such that for every collection Γ of curves in D the extremal length of Γ is at most K times the extremal length of { ƒ o γ : γ ∈ Γ }. Then ƒ is K-quasiconformal.
If ƒ is K-quasiconformal for some finite K, then ƒ is quasiconformal.
A few facts about quasiconformal mappings
Conformal homeomophisms are 1-quasiconformal and conversely, a 1-quasiconformal homeomorphism is conformal.The map
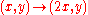 is 2-quasiconformal.
is 2-quasiconformal.The map
 is quasiconformal if
is quasiconformal if  (here
(here  is a complex number). This is an example of a quasiconformal homeomorphism that is not smooth. If
is a complex number). This is an example of a quasiconformal homeomorphism that is not smooth. If  , this is simply the identity map.
, this is simply the identity map.If
 is
is  quasiconformal and
quasiconformal and 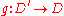 is
is 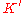 quasiconformal, then
quasiconformal, then  is
is 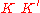 quasiconformal.
quasiconformal.The inverse of a K-quasiconformal homeomorphism is K-quasiconformal.
The space of K-quasiconformal mappings from the complex plane to itself mapping three distinct points to three given points is compact.
Measurable Riemann mapping theorem
Of central importance in the theory of quasiconformal mappings in two dimensions is the measurable Riemann mapping theoremMeasurable Riemann mapping theorem
In the mathematical theory of quasiconformal mappings in two dimensions, the measurable Riemann mapping theorem, proved by , generalizes the Riemann mapping theorem from conformal to quasiconformal homeomorphisms, and is stated as follows...
, proved by . The theorem generalizes the Riemann mapping theorem from conformal to quasiconformal homeomorphisms, and is stated as follows. Suppose that D is a simply connected domain in C that is not equal to C, and suppose that
 is Lebesgue measurable and satisfies
is Lebesgue measurable and satisfies  . Then there is a quasiconformal homeomorphism ƒ from D to the unit disk which is in the Sobolev space W1,2(D) and satisfies the corresponding Beltrami equation in the distributional sense
. Then there is a quasiconformal homeomorphism ƒ from D to the unit disk which is in the Sobolev space W1,2(D) and satisfies the corresponding Beltrami equation in the distributional senseWeak solution
In mathematics, a weak solution to an ordinary or partial differential equation is a function for which the derivatives may not all exist but which is nonetheless deemed to satisfy the equation in some precisely defined sense. There are many different definitions of weak solution, appropriate for...
. As with Riemann's mapping theorem, this ƒ is unique up to 3 real parameters.

