
Lattice (discrete subgroup)
Encyclopedia
In Lie theory
and related areas of mathematics
, a lattice in a locally compact topological group
is a discrete subgroup with the property that the quotient space
has finite invariant measure
. In the special case of subgroups of Rn, this amounts to the usual geometric notion of a lattice
, and both the algebraic structure of lattices and the geometry of the totality of all lattices are relatively well understood. Deep results of Borel
, Harish-Chandra
, Mostow
, Tamagawa
, M.S. Raghunathan, Margulis
, Zimmer obtained from the 1950s through the 1970s provided examples and generalized much of the theory to the setting of nilpotent
Lie group
s and semisimple algebraic group
s over a local field
. In the 1990s, Bass
and Lubotzky
initiated the study of tree lattices, which remains an active research area.
μ. A discrete subgroup Γ is called a lattice in G if the quotient space G/Γ has finite invariant measure, that is, if G is a unimodular group and the volume μ(G/Γ) is finite. The lattice is uniform (or cocompact) if the quotient space is compact
, and nonuniform otherwise.
SL(2,R), and by the closely related modular group
. This construction admits a far-reaching generalization to a class of lattices in all semisimple algebraic group
s over a local field
F called arithmetic lattices
. For example, let F = R be the field of real numbers. Roughly speaking, the Lie group
G(R) is formed by all matrices with entries in R satisfying certain algebraic conditions, and by restricting the entries to the integer
s Z, one obtains a lattice G(Z). Conversely, Grigory Margulis
proved that under certain assumptions on G, any lattice in it essentially arises in this way. This remarkable statement is known as Arithmeticity of lattices or Margulis Arithmeticity Theorem.
Lie theory
Lie theory is an area of mathematics, developed initially by Sophus Lie.Early expressions of Lie theory are found in books composed by Lie with Friedrich Engel and Georg Scheffers from 1888 to 1896....
and related areas of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a lattice in a locally compact topological group
Topological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
is a discrete subgroup with the property that the quotient space
Quotient space
In topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...
has finite invariant measure
Invariant measure
In mathematics, an invariant measure is a measure that is preserved by some function. Ergodic theory is the study of invariant measures in dynamical systems...
. In the special case of subgroups of Rn, this amounts to the usual geometric notion of a lattice
Lattice (group)
In mathematics, especially in geometry and group theory, a lattice in Rn is a discrete subgroup of Rn which spans the real vector space Rn. Every lattice in Rn can be generated from a basis for the vector space by forming all linear combinations with integer coefficients...
, and both the algebraic structure of lattices and the geometry of the totality of all lattices are relatively well understood. Deep results of Borel
Armand Borel
Armand Borel was a Swiss mathematician, born in La Chaux-de-Fonds, and was a permanent professor at the Institute for Advanced Study in Princeton, New Jersey, United States from 1957 to 1993...
, Harish-Chandra
Harish-Chandra
Harish-Chandra was an Indian mathematician, who did fundamental work in representation theory, especially Harmonic analysis on semisimple Lie groups. -Life:...
, Mostow
George Mostow
George Mostow is an American mathematician, a member of the National Academy of Sciences, Henry Ford II Professor of Mathematics at Yale University, the 49th President of the American Mathematical Society ,...
, Tamagawa
Tsuneo Tamagawa
Tsuneo Tamagawa is a mathematician. He works on the arithmetic of classical groups.He has been on the Yale University faculty since 1963, and became emeritus in 1996.-References:*...
, M.S. Raghunathan, Margulis
Grigory Margulis
Gregori Aleksandrovich Margulis is a Russian mathematician known for his far-reaching work on lattices in Lie groups, and the introduction of methods from ergodic theory into diophantine approximation. He was awarded a Fields Medal in 1978 and a Wolf Prize in Mathematics in 2005, becoming the...
, Zimmer obtained from the 1950s through the 1970s provided examples and generalized much of the theory to the setting of nilpotent
Nilpotent group
In mathematics, more specifically in the field of group theory, a nilpotent group is a group that is "almost abelian". This idea is motivated by the fact that nilpotent groups are solvable, and for finite nilpotent groups, two elements having relatively prime orders must commute...
Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s and semisimple algebraic group
Semisimple algebraic group
In mathematics, especially in the areas of abstract algebra and algebraic geometry studying linear algebraic groups, a semisimple algebraic group is a type of matrix group which behaves much like a semisimple Lie algebra or semisimple ring.- Definition :...
s over a local field
Local field
In mathematics, a local field is a special type of field that is a locally compact topological field with respect to a non-discrete topology.Given such a field, an absolute value can be defined on it. There are two basic types of local field: those in which the absolute value is archimedean and...
. In the 1990s, Bass
Hyman Bass
Hyman Bass is an American mathematician, known for work in algebra and in mathematics education. From 1959-1998 he was Professor in the Mathematics Department at Columbia University, where he is now professor emeritus...
and Lubotzky
Alexander Lubotzky
Professor Alexander Lubotzky is an Israeli academic and former politician. A former head of the Mathematics Institute at the Hebrew University of Jerusalem, he served as a member of the Knesset for The Third Way party between 1996 and 1999.-Education:...
initiated the study of tree lattices, which remains an active research area.
Definition
Let G be a locally compact topological group with the Haar measureHaar measure
In mathematical analysis, the Haar measure is a way to assign an "invariant volume" to subsets of locally compact topological groups and subsequently define an integral for functions on those groups....
μ. A discrete subgroup Γ is called a lattice in G if the quotient space G/Γ has finite invariant measure, that is, if G is a unimodular group and the volume μ(G/Γ) is finite. The lattice is uniform (or cocompact) if the quotient space is compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
, and nonuniform otherwise.
Arithmetic lattices
An archetypical example of a nonuniform lattice is given by the group SL(2,Z), which is a lattice in the special linear groupSpecial linear group
In mathematics, the special linear group of degree n over a field F is the set of n×n matrices with determinant 1, with the group operations of ordinary matrix multiplication and matrix inversion....
SL(2,R), and by the closely related modular group
Modular group
In mathematics, the modular group Γ is a fundamental object of study in number theory, geometry, algebra, and many other areas of advanced mathematics...
. This construction admits a far-reaching generalization to a class of lattices in all semisimple algebraic group
Semisimple algebraic group
In mathematics, especially in the areas of abstract algebra and algebraic geometry studying linear algebraic groups, a semisimple algebraic group is a type of matrix group which behaves much like a semisimple Lie algebra or semisimple ring.- Definition :...
s over a local field
Local field
In mathematics, a local field is a special type of field that is a locally compact topological field with respect to a non-discrete topology.Given such a field, an absolute value can be defined on it. There are two basic types of local field: those in which the absolute value is archimedean and...
F called arithmetic lattices
Arithmetic group
In mathematics, an arithmetic group in a linear algebraic group G defined over a number field K is a subgroup Γ of G that is commensurable with G, where O is the ring of integers of K. Here two subgroups A and B of a group are commensurable when their intersection has finite index in each of them...
. For example, let F = R be the field of real numbers. Roughly speaking, the Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
G(R) is formed by all matrices with entries in R satisfying certain algebraic conditions, and by restricting the entries to the integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s Z, one obtains a lattice G(Z). Conversely, Grigory Margulis
Grigory Margulis
Gregori Aleksandrovich Margulis is a Russian mathematician known for his far-reaching work on lattices in Lie groups, and the introduction of methods from ergodic theory into diophantine approximation. He was awarded a Fields Medal in 1978 and a Wolf Prize in Mathematics in 2005, becoming the...
proved that under certain assumptions on G, any lattice in it essentially arises in this way. This remarkable statement is known as Arithmeticity of lattices or Margulis Arithmeticity Theorem.
S-arithmetic lattices
Arithmetic lattices admit an important generalization, known as the S-arithmetic lattices. The first example is given by the diagonally embedded subgroup-
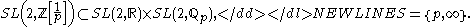
This is a lattice in the product of algebraic groups over different local fields, both real and p-adicP-adic numberIn mathematics, and chiefly number theory, the p-adic number system for any prime number p extends the ordinary arithmetic of the rational numbers in a way different from the extension of the rational number system to the real and complex number systems...
. It is formed by the unimodular matrices of order 2 with entries in the localizationLocalization of a ringIn abstract algebra, localization is a systematic method of adding multiplicative inverses to a ring. Given a ring R and a subset S, one wants to construct some ring R* and ring homomorphism from R to R*, such that the image of S consists of units in R*...
of the ring of integers at the prime p. The set S is a finite set of places of Q which includes all archimedean places and the locally compact group is the direct product of the groups of points of a fixed linear algebraic group G defined over Q (or a more general global fieldGlobal fieldIn mathematics, the term global field refers to either of the following:*an algebraic number field, i.e., a finite extension of Q, or*a global function field, i.e., the function field of an algebraic curve over a finite field, equivalently, a finite extension of Fq, the field of rational functions...
) over the completions of Q at the places from S. To form the discrete subgroup, instead of matrices with integer entries, one considers matrices with entries in the localizationLocalization of a ringIn abstract algebra, localization is a systematic method of adding multiplicative inverses to a ring. Given a ring R and a subset S, one wants to construct some ring R* and ring homomorphism from R to R*, such that the image of S consists of units in R*...
over the primes (nonarchimedean places) in S. Under fairly general assumptions, this construction indeed produces a lattice. The class of S-arithmetic lattices is much wider than the class of arithmetic lattices, but they share many common features.
Adelic case
A lattice of fundamental importance for the theory of automorphic formAutomorphic formIn mathematics, the general notion of automorphic form is the extension to analytic functions, perhaps of several complex variables, of the theory of modular forms...
s is given by the group G(K) of K-points of a semisimple (or reductive) linear algebraic group G defined over a global field K. This group diagonally embeds into the adelic algebraic groupAdelic algebraic groupIn abstract algebra, an adelic algebraic group is a topological group defined by an algebraic group G over a number field K, and the adele ring A = A of K. It consists of the points of G having values in A; the definition of the appropriate topology is straightforward only in case G is a linear...
G(A), where A is the ring of adelesAdele ringIn algebraic number theory and topological algebra, the adele ring is a topological ring which is built on the field of rational numbers . It involves all the completions of the field....
of K, and is a lattice there. Unlike arithmetic lattices, G(K) is not finitely generated.
Rigidity
Another group of phenomena concerning lattices in semisimple algebraic groups is collectively known as rigidity. The Mostow rigidity theoremMostow rigidity theoremIn mathematics, Mostow's rigidity theorem, or strong rigidity theorem, or Mostow–Prasad rigidity theorem, essentially states that the geometry of a finite-volume hyperbolic manifold of dimension greater than two is determined by the fundamental group and hence unique...
showed that the algebraic structure of a lattice in simple Lie group G of split rank at least two determines G. Thus any isomorphism of lattices in two such groups is essentially induced by an isomorphism between the groups themselves. SuperrigiditySuperrigidityIn mathematics, in the theory of discrete groups, superrigidity is a concept designed to show how a linear representation ρ of a discrete group Γ inside an algebraic group G can, under some circumstances, be as good as a representation of G itself...
provides a generalization dealing with homomorphisms from a lattice in an algebraic group G into another algebraic group H.
Tree lattices
Let X be a locally finite tree. Then the automorphism group G of X is a locally compact topological group, in which the basis of the topology is given by the stabilizers of finite sets of vertices. Vertex stabilizers Gx are thus compact open subgroups, and a subgroup Γ of G is discrete if Γx is finite for some (and hence, for any) vertex x. The subgroup Γ is an X-lattice if the suitably defined
volume of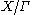 is finite, and a uniform X-lattice if this quotient is a finite graph. In case
is finite, and a uniform X-lattice if this quotient is a finite graph. In case 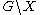 is finite, this is equivalent to Γ being a lattice (respectively, a uniform lattice) in G.
is finite, this is equivalent to Γ being a lattice (respectively, a uniform lattice) in G.

