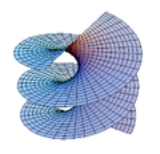
The helicoid, after the plane and the catenoid

Catenoid

A catenoid is a three-dimensional surface made by rotating a catenary curve about its directrix. Not counting the plane, it is the first minimal surface to be discovered. It was found and proved to be minimal by Leonhard Euler in 1744. Early work on the subject was published also by Jean Baptiste...

, is the third minimal surface

Minimal surface

In mathematics, a minimal surface is a surface with a mean curvature of zero.These include, but are not limited to, surfaces of minimum area subject to various constraints....

 to be known. It was first discovered by Jean Baptiste Meusnier

Jean Baptiste Meusnier

Jean Baptiste Marie Charles Meusnier de la Place was a French mathematician, engineer and Revolutionary general. He is best known for Meusnier's theorem on the curvature of surfaces, which he formulated while he was at the École Royale du Génie . He also discovered the helicoid...

 in 1776. Its name

Nomenclature

Nomenclature is a term that applies to either a list of names or terms, or to the system of principles, procedures and terms related to naming - which is the assigning of a word or phrase to a particular object or property...

 derives from its similarity to the helix

Helix

A helix is a type of smooth space curve, i.e. a curve in three-dimensional space. It has the property that the tangent line at any point makes a constant angle with a fixed line called the axis. Examples of helixes are coil springs and the handrails of spiral staircases. A "filled-in" helix – for...

: for every point

Point (geometry)

In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...

 on the helicoid there is a helix contained in the helicoid which passes through that point. Since it is considered that the planar range extends through negative and positive infinity, close observation shows the appearance of two parallel or mirror planes in the sense that if the slope of one plane is traced, the co-plane can be seen to be bypassed or skipped, though in actuality the co-plane is also traced from the opposite perspective.

The helicoid is also a ruled surface

Ruled surface

In geometry, a surface S is ruled if through every point of S there is a straight line that lies on S. The most familiar examples are the plane and the curved surface of a cylinder or cone...

 (and a right conoid

Right conoid

In geometry, a right conoid is a ruled surface generated by a family of straight lines that all intersect perpendicularly a fixed straight line, called the axis of the right conoid....

), meaning that it is a trace of a line.