Catenoid
Encyclopedia
A catenoid is a three-dimension
al surface
made by rotating a catenary
curve
about its directrix. Not counting the plane, it is the first minimal surface
to be discovered. It was found and proved to be minimal by Leonhard Euler
in 1744. Early work on the subject was published also by Jean Baptiste Meusnier
. There are only two surfaces of revolution
which are also minimal surfaces: the plane and the catenoid.
The catenoid may be defined by the following parametric equations:
In cylindrical coordinates:
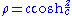
A physical model of a catenoid can be formed by dipping two circle
s into a soap solution and slowly drawing the circles apart.
One can bend a catenoid into the shape of a helicoid
without stretching. In other words, one can make a continuous
and isometric
deformation of a catenoid to a helicoid
such that every member of the deformation family is minimal
(having a mean curvature
of zero). A parametrization
of such a deformation is given by the system
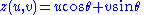
where
corresponds to a right-handed helicoid,
corresponds to a catenoid, and
corresponds to a left-handed helicoid.
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
al surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
made by rotating a catenary
Catenary
In physics and geometry, the catenary is the curve that an idealised hanging chain or cable assumes when supported at its ends and acted on only by its own weight. The curve is the graph of the hyperbolic cosine function, and has a U-like shape, superficially similar in appearance to a parabola...
curve
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
about its directrix. Not counting the plane, it is the first minimal surface
Minimal surface
In mathematics, a minimal surface is a surface with a mean curvature of zero.These include, but are not limited to, surfaces of minimum area subject to various constraints....
to be discovered. It was found and proved to be minimal by Leonhard Euler
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
in 1744. Early work on the subject was published also by Jean Baptiste Meusnier
Jean Baptiste Meusnier
Jean Baptiste Marie Charles Meusnier de la Place was a French mathematician, engineer and Revolutionary general. He is best known for Meusnier's theorem on the curvature of surfaces, which he formulated while he was at the École Royale du Génie . He also discovered the helicoid...
. There are only two surfaces of revolution
Surface of revolution
A surface of revolution is a surface in Euclidean space created by rotating a curve around a straight line in its plane ....
which are also minimal surfaces: the plane and the catenoid.
The catenoid may be defined by the following parametric equations:
- where u and v are real parameters and c is a non-zero real constant.
In cylindrical coordinates:
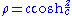
- Where c is a real constant.
A physical model of a catenoid can be formed by dipping two circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
s into a soap solution and slowly drawing the circles apart.
Helicoid transformation
Helicoid
The helicoid, after the plane and the catenoid, is the third minimal surface to be known. It was first discovered by Jean Baptiste Meusnier in 1776. Its name derives from its similarity to the helix: for every point on the helicoid there is a helix contained in the helicoid which passes through...
without stretching. In other words, one can make a continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
and isometric
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
deformation of a catenoid to a helicoid
Helicoid
The helicoid, after the plane and the catenoid, is the third minimal surface to be known. It was first discovered by Jean Baptiste Meusnier in 1776. Its name derives from its similarity to the helix: for every point on the helicoid there is a helix contained in the helicoid which passes through...
such that every member of the deformation family is minimal
Minimal surface
In mathematics, a minimal surface is a surface with a mean curvature of zero.These include, but are not limited to, surfaces of minimum area subject to various constraints....
(having a mean curvature
Mean curvature
In mathematics, the mean curvature H of a surface S is an extrinsic measure of curvature that comes from differential geometry and that locally describes the curvature of an embedded surface in some ambient space such as Euclidean space....
of zero). A parametrization
Parametric equation
In mathematics, parametric equation is a method of defining a relation using parameters. A simple kinematic example is when one uses a time parameter to determine the position, velocity, and other information about a body in motion....
of such a deformation is given by the system
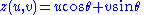
- for
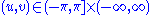, with deformation parameter 
,
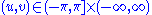where
corresponds to a right-handed helicoid, corresponds to a catenoid, and corresponds to a left-handed helicoid.