
Geodesic
Encyclopedia
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a geodesic (icon or ˌ ) is a generalization of the notion of a "straight line
Line (mathematics)
The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
" to "curved space
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
s". In the presence of a Riemannian metric, geodesics are defined to be (locally) the shortest path between points in the space. In the presence of an affine connection
Affine connection
In the branch of mathematics called differential geometry, an affine connection is a geometrical object on a smooth manifold which connects nearby tangent spaces, and so permits tangent vector fields to be differentiated as if they were functions on the manifold with values in a fixed vector space...
, geodesics are defined to be curves whose tangent vector
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
s remain parallel if they are transported
Parallel transport
In geometry, parallel transport is a way of transporting geometrical data along smooth curves in a manifold. If the manifold is equipped with an affine connection , then this connection allows one to transport vectors of the manifold along curves so that they stay parallel with respect to the...
along it.
The term "geodesic" comes from geodesy
Geodesy
Geodesy , also named geodetics, a branch of earth sciences, is the scientific discipline that deals with the measurement and representation of the Earth, including its gravitational field, in a three-dimensional time-varying space. Geodesists also study geodynamical phenomena such as crustal...
, the science of measuring the size and shape of Earth
Earth
Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
; in the original sense, a geodesic was the shortest route between two points on the Earth's surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
, namely, a segment
Line segment
In geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...
of a great circle
Great circle
A great circle, also known as a Riemannian circle, of a sphere is the intersection of the sphere and a plane which passes through the center point of the sphere, as opposed to a general circle of a sphere where the plane is not required to pass through the center...
. The term has been generalized to include measurements in much more general mathematical spaces; for example, in graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, one might consider a geodesic between two vertices/nodes of a graph.
Geodesics are of particular importance in general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, as they describe the motion of inertial test particles.
Introduction
The shortest path between two points in a curved space can be found by writing the equationEquation
An equation is a mathematical statement that asserts the equality of two expressions. In modern notation, this is written by placing the expressions on either side of an equals sign , for examplex + 3 = 5\,asserts that x+3 is equal to 5...
for the length of a curve
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
(a function f from an open interval of R to the manifold), and then minimizing this length using the calculus of variations
Calculus of variations
Calculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
. This has some minor technical problems, because there is an infinite dimensional space of different ways to parameterize the shortest path. It is simpler to demand not only that the curve locally minimize length but also that it is parameterized "with constant velocity", meaning that the distance from f(s) to f(t) along the geodesic is proportional to |s−t|. Equivalently, a different quantity may be defined, termed the energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
of the curve; minimizing the energy leads to the same equations for a geodesic (here "constant velocity" is a consequence of minimisation). Intuitively, one can understand this second formulation by noting that an elastic band stretched between two points will contract its length, and in so doing will minimize its energy. The resulting shape of the band is a geodesic.
In Riemannian geometry geodesics are not the same as "shortest curves" between two points, though the two concepts are closely related. The difference is that geodesics are only locally the shortest distance between points, and are parameterized with "constant velocity". Going the "long way round" on a great circle between two points on a sphere is a geodesic but not the shortest path between the points. The map t → t2 from the unit interval to itself gives the shortest path between 0 and 1, but is not a geodesic because the velocity of the corresponding motion of a point is not constant.
Geodesics are commonly seen in the study of Riemannian geometry
Riemannian geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
and more generally metric geometry. In general relativity, geodesics describe the motion of point particle
Point particle
A point particle is an idealization of particles heavily used in physics. Its defining feature is that it lacks spatial extension: being zero-dimensional, it does not take up space...
s under the influence of gravity alone. In particular, the path taken by a falling rock, an orbiting satellite
Satellite
In the context of spaceflight, a satellite is an object which has been placed into orbit by human endeavour. Such objects are sometimes called artificial satellites to distinguish them from natural satellites such as the Moon....
, or the shape of a planetary orbit
Planetary orbit
In physics, an orbit is the gravitationally curved path of an object around a point in space, for example the orbit of a planet around the center of a star system, such as the Solar System...
are all geodesics in curved space-time. More generally, the topic of sub-Riemannian geometry deals with the paths that objects may take when they are not free, and their movement is constrained in various ways.
This article presents the mathematical formalism involved in defining, finding, and proving the existence of geodesics, in the case of Riemannian
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
and pseudo-Riemannian manifold
Pseudo-Riemannian manifold
In differential geometry, a pseudo-Riemannian manifold is a generalization of a Riemannian manifold. It is one of many mathematical objects named after Bernhard Riemann. The key difference between a Riemannian manifold and a pseudo-Riemannian manifold is that on a pseudo-Riemannian manifold the...
s. The article geodesic (general relativity)
Geodesic (general relativity)
In general relativity, a geodesic generalizes the notion of a "straight line" to curved spacetime. Importantly, the world line of a particle free from all external, non-gravitational, force is a particular type of geodesic...
discusses the special case of general relativity in greater detail.
Examples
The most familiar examples are the straight lines in Euclidean geometryEuclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
.
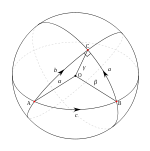
On a sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
, the images of geodesics are the great circle
Great circle
A great circle, also known as a Riemannian circle, of a sphere is the intersection of the sphere and a plane which passes through the center point of the sphere, as opposed to a general circle of a sphere where the plane is not required to pass through the center...
s.
The shortest path from point A to point B on a sphere is given by the shorter arc of the great circle passing through A and B. If A and B are antipodal point
Antipodal point
In mathematics, the antipodal point of a point on the surface of a sphere is the point which is diametrically opposite to it — so situated that a line drawn from the one to the other passes through the centre of the sphere and forms a true diameter....
s (like the North pole and the South pole), then there are infinitely many shortest paths between them.
Metric geometry
In metric geometry, a geodesic is a curve which is everywhere locally a distanceDistance
Distance is a numerical description of how far apart objects are. In physics or everyday discussion, distance may refer to a physical length, or an estimation based on other criteria . In mathematics, a distance function or metric is a generalization of the concept of physical distance...
minimizer. More precisely, a curve
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
γ: I → M from an interval I of the reals to the metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
M is a geodesic if there is a constant
Mathematical constant
A mathematical constant is a special number, usually a real number, that is "significantly interesting in some way". Constants arise in many different areas of mathematics, with constants such as and occurring in such diverse contexts as geometry, number theory and calculus.What it means for a...
v ≥ 0 such that for any t ∈ I there is a neighborhood J of t in I such that for any we have

This generalizes the notion of geodesic for Riemannian manifolds. However, in metric geometry the geodesic considered is often equipped with natural parameterization, i.e. in the above identity v = 1 and
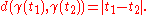
If the last equality is satisfied for all t1, t2 ∈I, the geodesic is called a minimizing geodesic or shortest path.
In general, a metric space may have no geodesics, except constant curves. At the other extreme, any two points in a length metric space are joined by a minimizing sequence of rectifiable paths, although this minimizing sequence need not converge to a geodesic.
Riemannian geometry
In a Riemannian manifoldRiemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
M with metric tensor
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
g, the length of a continuously differentiable curve γ : [a,b] → M is defined by

The distance d(p, q) between two points p and q of M is defined as the infimum
Infimum
In mathematics, the infimum of a subset S of some partially ordered set T is the greatest element of T that is less than or equal to all elements of S. Consequently the term greatest lower bound is also commonly used...
of the length taken over all continuous, piecewise continuously differentiable curves γ : [a,b] → M such that γ(a) = p and γ(b) = q. With this definition of distance, geodesics in a Riemannian manifold are then the locally distance-minimizing paths, in the above sense.
The minimizing curves of L in a small enough open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
of M can be obtained by techniques of calculus of variations
Calculus of variations
Calculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
. Typically, one introduces the following action
Action (physics)
In physics, action is an attribute of the dynamics of a physical system. It is a mathematical functional which takes the trajectory, also called path or history, of the system as its argument and has a real number as its result. Action has the dimension of energy × time, and its unit is...
or energy functional
Energy functional
Energy functional is total energy of a certain system, as a function of the system's state.In the energy methods of simulating the dynamics of complex structures, a state of the system is often described as an element of an appropriate function space. To be in this state, the system pays a certain...
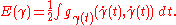
It is then enough to minimize the functional E, owing to the Cauchy–Schwarz inequality
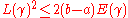
with equality if and only if |dγ/dt| is constant.
The Euler–Lagrange equations of motion for the functional E are then given in local coordinates by

where
 are the Christoffel symbols
are the Christoffel symbolsChristoffel symbols
In mathematics and physics, the Christoffel symbols, named for Elwin Bruno Christoffel , are numerical arrays of real numbers that describe, in coordinates, the effects of parallel transport in curved surfaces and, more generally, manifolds. As such, they are coordinate-space expressions for the...
of the metric. This is the geodesic equation, discussed below.
Calculus of variations
Techniques of the classical calculus of variationsCalculus of variations
Calculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
can be applied to examine the energy functional E. The first variation
First variation
In applied mathematics and the calculus of variations, the first variation of a functional J is defined as the linear functional \delta J mapping the function h to...
of energy is defined in local coordinates by
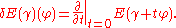
The critical point
Critical point (mathematics)
In calculus, a critical point of a function of a real variable is any value in the domain where either the function is not differentiable or its derivative is 0. The value of the function at a critical point is a critical value of the function...
s of the first variation are precisely the geodesics. The second variation is defined by

In an appropriate sense, zeros of the second variation along a geodesic γ arise along Jacobi field
Jacobi field
In Riemannian geometry, a Jacobi field is a vector field along a geodesic \gamma in a Riemannian manifold describing the difference between the geodesic and an "infinitesimally close" geodesic. In other words, the Jacobi fields along a geodesic form the tangent space to the geodesic in the space...
s. Jacobi fields are thus regarded as variations through geodesics.
By applying variational techniques from classical mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
, one can also regard geodesics as Hamiltonian flows
Geodesics as Hamiltonian flows
In mathematics, the geodesic equations are second-order non-linear differential equations, and are commonly presented in the form of Euler–Lagrange equations of motion. However, they can also be presented as a set of coupled first-order equations, in the form of Hamilton's equations...
. They are solutions of the associated Hamilton–Jacobi equation
Hamilton–Jacobi equation
In mathematics, the Hamilton–Jacobi equation is a necessary condition describing extremal geometry in generalizations of problems from the calculus of variations. In physics, the Hamilton–Jacobi equation is a reformulation of classical mechanics and, thus, equivalent to other formulations such as...
s, with (pseudo-)Riemannian metric taken as Hamiltonian
Hamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
.
Affine geodesics
A geodesic on a smooth manifold M with an affine connectionAffine connection
In the branch of mathematics called differential geometry, an affine connection is a geometrical object on a smooth manifold which connects nearby tangent spaces, and so permits tangent vector fields to be differentiated as if they were functions on the manifold with values in a fixed vector space...
∇ is defined as a curve
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
γ(t) such that parallel transport
Parallel transport
In geometry, parallel transport is a way of transporting geometrical data along smooth curves in a manifold. If the manifold is equipped with an affine connection , then this connection allows one to transport vectors of the manifold along curves so that they stay parallel with respect to the...
along the curve preserves the tangent vector to the curve, so
at each point along the curve, where
 is the derivative with respect to
is the derivative with respect to  . More precisely, in order to define the covariant derivative of
. More precisely, in order to define the covariant derivative of  it is necessary first to extend
it is necessary first to extend  to a continuously differentiable vector field
to a continuously differentiable vector fieldVector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
in an open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
. However, the resulting value of is independent of the choice of extension.
Using local coordinates
Local coordinates
Local coordinates are measurement indices into a local coordinate system or a local coordinate space. A simple example is using house numbers to locate a house on a street; the street is a local coordinate system within a larger system composed of city townships, states, countries, etc.Local...
on M, we can write the geodesic equation (using the summation convention) as
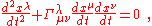
where
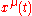 are the coordinates of the curve γ(t) and
are the coordinates of the curve γ(t) and 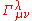 are the Christoffel symbols of the connection ∇. This is just an ordinary differential equation
are the Christoffel symbols of the connection ∇. This is just an ordinary differential equationOrdinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
for the coordinates. It has a unique solution, given an initial position and an initial velocity. Therefore, from the point of view of classical mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
, geodesics can be thought of as trajectories of free particle
Free particle
In physics, a free particle is a particle that, in some sense, is not bound. In classical physics, this means the particle is present in a "field-free" space.-Classical Free Particle:The classical free particle is characterized simply by a fixed velocity...
s in a manifold. Indeed, the equation
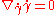 means that the acceleration of the curve has no components in the direction of the surface (and therefore it is perpendicular to the tangent plane of the surface at each point of the curve). So, the motion is completely determined by the bending of the surface. This is also the idea of the general relativity where particles move on geodesics and the bending is caused by the gravity.
means that the acceleration of the curve has no components in the direction of the surface (and therefore it is perpendicular to the tangent plane of the surface at each point of the curve). So, the motion is completely determined by the bending of the surface. This is also the idea of the general relativity where particles move on geodesics and the bending is caused by the gravity.Existence and uniqueness
The local existence and uniqueness theorem for geodesics states that geodesics on a smooth manifold with an affine connection exist, and are unique. More precisely:- For any point p in M and for any vector V in TpM (the tangent spaceTangent spaceIn mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
to M at p) there exists a unique geodesic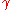 : I → M such that
: I → M such that
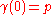 and
and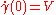 ,
,
- where I is a maximal open interval in R containing 0.
In general, I may not be all of R as for example for an open disc in R2.
The proof of this theorem follows from the theory of ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
s, by noticing that the geodesic equation is a second-order ODE. Existence and uniqueness then follow from the Picard–Lindelöf theorem for the solutions of ODEs with prescribed initial conditions. γ depends smoothly
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
on both p and V.
Geodesic flow
Geodesic flowFlow (mathematics)
In mathematics, a flow formalizes the idea of the motion of particles in a fluid. Flows are ubiquitous in science, including engineering and physics. The notion of flow is basic to the study of ordinary differential equations. Informally, a flow may be viewed as a continuous motion of points over...
is a local R-action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
on tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
TM of a manifold M defined in the following way
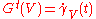
where t ∈ R, V ∈ TM and
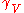 denotes the geodesic with initial data
denotes the geodesic with initial data  . Thus, Gt(V) = exp(tV) is the exponential map
. Thus, Gt(V) = exp(tV) is the exponential mapExponential map
In differential geometry, the exponential map is a generalization of the ordinary exponential function of mathematical analysis to all differentiable manifolds with an affine connection....
of the vector tV. A closed orbit of the geodesic flow corresponds to a closed geodesic
Closed geodesic
In differential geometry and dynamical systems, a closed geodesic on a Riemannian manifold M is the projection of a closed orbit of the geodesic flow on M.-Examples:On the unit sphere, every great circle is an example of a closed geodesic...
on M.
On a (pseudo-)Riemannian manifold, the geodesic flow is identified with a Hamiltonian flow on the cotangent bundle. The Hamiltonian
Hamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
is then given by the inverse of the (pseudo-)Riemannian metric, evaluated against the canonical one-form. In particular the flow preserves the (pseudo-)Riemannian metric
 , i.e.
, i.e.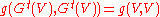 .
.In particular, when V is a unit vector,
 remains unit speed throughout, so the geodesic flow is tangent to the unit tangent bundle
remains unit speed throughout, so the geodesic flow is tangent to the unit tangent bundleUnit tangent bundle
In Riemannian geometry, a branch of mathematics, the unit tangent bundle of a Riemannian manifold , denoted by UT or simply UTM, is the unit sphere bundle for the tangent bundle T...
. Liouville's theorem
Liouville's theorem (Hamiltonian)
In physics, Liouville's theorem, named after the French mathematician Joseph Liouville, is a key theorem in classical statistical and Hamiltonian mechanics...
implies invariance of a kinematic measure on the unit tangent bundle.
Geodesic spray
The geodesic flow defines a family of curves in the tangent bundleTangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
. The derivatives of these curves define a vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
on the total space of the tangent bundle, known as the geodesic spray
Spray (mathematics)
In differential geometry, a spray is a vector field H on the tangent bundle TM that encodes a quasilinear second order system of ordinary differential equations on the base manifold M. Usually a spray is required to be homogeneous in the sense that its integral curves t→ΦHt∈TM obey the rule...
.
More precisely, an affine connection gives rise to a splitting of the double tangent bundle
Double tangent bundle
In mathematics, particularly differential topology, the double tangent bundle or the second tangent bundle refers to the tangent bundle of the total space TM of the tangent bundle of a smooth manifold M...
TTM into horizontal
Horizontal bundle
In mathematics, in the field of differential topology, givena smooth fiber bundle over a smooth manifold M, then the vertical bundle VE of E is the subbundle of the tangent bundle TE consisting of the vectors which are tangent to the fibers of E over M...
and vertical bundle
Vertical bundle
The vertical bundle of a smooth fiber bundle is the subbundle of the tangent bundle that consists of all vectors which are tangent to the fibers...
s:

The geodesic spray is the unique horizontal vector field W satisfying
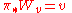
at each point v ∈ TM; here π∗ : TTM → TM denotes the pushforward (differential) along the projection π : TM → M associated to the tangent bundle.
More generally, the same construction allows one to construct a vector field for any Ehresmann connection
Ehresmann connection
In differential geometry, an Ehresmann connection is a version of the notion of a connection, which makes sense on any smooth fibre bundle...
on the tangent bundle. For the resulting vector field to be a spray (on the deleted tangent bundle TM \ {0}) it is enough that the connection be equivariant under positive rescalings: it need not be linear. That is, (cf. Ehresmann connection#Vector bundles and covariant derivatives) it is enough that the horizontal distribution satisfy
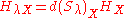
for every X ∈ TM \ {0} and λ > 0. Here d(Sλ) is the pushforward along the scalar homothety
 A particular case of a non-linear connection arising in this manner is that associated to a Finsler manifold
A particular case of a non-linear connection arising in this manner is that associated to a Finsler manifoldFinsler manifold
In mathematics, particularly differential geometry, a Finsler manifold is a differentiable manifold together with the structure of an intrinsic quasimetric space in which the length of any rectifiable curve is given by the length functional...
.
Affine and projective geodesics
Equation is invariant under affine reparameterizations; that is, parameterizations of the form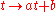
where a and b are constant real numbers. Thus apart from specifying a certain class of embedded curves, the geodesic equation also determines a preferred class of parameterizations on each of the curves. Accordingly, solutions of are called geodesics with affine parameter.
An affine connection is determined by its family of affinely parameterized geodesics, up to torsion
Torsion tensor
In differential geometry, the notion of torsion is a manner of characterizing a twist or screw of a moving frame around a curve. The torsion of a curve, as it appears in the Frenet-Serret formulas, for instance, quantifies the twist of a curve about its tangent vector as the curve evolves In the...
. The torsion itself does not, in fact, affect the family of geodesics, since the geodesic equation depends only on the symmetric part of the connection. More precisely, if
 are two connections such that the difference tensor
are two connections such that the difference tensor
is skew-symmetric, then
 and
and  have the same geodesics, with the same affine parameterizations. Furthermore, there is a unique connection having the same geodesics as
have the same geodesics, with the same affine parameterizations. Furthermore, there is a unique connection having the same geodesics as  , but with vanishing torsion.
, but with vanishing torsion.Geodesics without a particular parameterization are described by a projective connection
Projective connection
In differential geometry, a projective connection is a type of Cartan connection on a differentiable manifold.The structure of a projective connection is modeled on the geometry of projective space, rather than the affine space corresponding to an affine connection. Much like affine connections,...
.
External links
- Caltech Tutorial on Relativity — A nice, simple explanation of geodesics with accompanying animation.

