Double coset
Encyclopedia
In mathematics
, an (H,K) double coset in G, where G is a group
and H and K are subgroup
s of G, is an equivalence class for the equivalence relation
defined on G by
Then each double coset is of form HxK, and G is partitioned into its (H,K) double cosets; each of them is a union of ordinary right coset
s Hy of H in G and left cosets zK of K in G. In another aspect, these are in fact orbits for the group action of H×K on G with H acting by left multiplication and K by inverse right multiplication. The space of double cosets can be written
Given two double cosets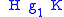
and 
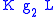, we decompose each into right cosets 
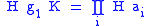and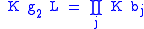 
. If we write 
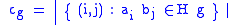, then we can define the product of 
with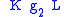 
as the formal sum
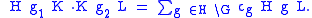
An important case is when H = K = L, which allows us to define an algebra structure on the associated ring spanned by linear combinations of double cosets.
, when a representation of H is used to construct an induced representation
of G, which is then restricted
to K. The corresponding double coset structure carries information about how the resulting representation decomposes.
They are also important in functional analysis
, where in some important cases functions left-invariant and right-invariant by a subgroup K can form a commutative ring
under convolution
: see Gelfand pair
.
In geometry, a Clifford–Klein form is a double coset space Γ\G/H, where G is a reductive Lie group, H is a closed subgroup, and Γ is a discrete subgroup (of G) that acts properly discontinuously on the homogeneous space
G/H.
In number theory
, the Hecke algebra
corresponding to a congruence subgroup
Γ of the modular group
is spanned by elements of the double coset space
; the algebra structure is that acquired from the multiplication of double cosets described above. Of particular importance are the Hecke operators 
corresponding to the double cosets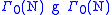 
or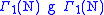 
, where 
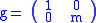(these have different properties depending on whether m and N are coprime or not), and the diamond operators 
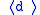given by the double cosets 
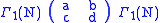where 
and we require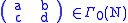 
(the choice of a, b, c does not affect the answer).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an (H,K) double coset in G, where G is a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
and H and K are subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
s of G, is an equivalence class for the equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
defined on G by
- x ~ y if there are h in H and k in K with hxk = y.
Then each double coset is of form HxK, and G is partitioned into its (H,K) double cosets; each of them is a union of ordinary right coset
Coset
In mathematics, if G is a group, and H is a subgroup of G, and g is an element of G, thenA coset is a left or right coset of some subgroup in G...
s Hy of H in G and left cosets zK of K in G. In another aspect, these are in fact orbits for the group action of H×K on G with H acting by left multiplication and K by inverse right multiplication. The space of double cosets can be written
- H\G/K.
Algebraic structure
It is possible to define a kind of product of double cosets in an associated ring.Given two double cosets
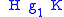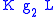and , we decompose each into right cosets 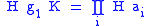and 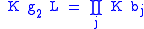. If we write 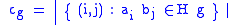, then we can define the product of with 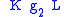as the formal sum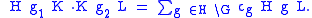An important case is when H = K = L, which allows us to define an algebra structure on the associated ring spanned by linear combinations of double cosets.
Applications
Double cosets are important in connection with representation theoryRepresentation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
, when a representation of H is used to construct an induced representation
Induced representation
In mathematics, and in particular group representation theory, the induced representation is one of the major general operations for passing from a representation of a subgroup H to a representation of the group G itself. It was initially defined as a construction by Frobenius, for linear...
of G, which is then restricted
Restricted representation
In mathematics, restriction is a fundamental construction in representation theory of groups. Restriction forms a representation of a subgroup from a representation of the whole group. Often the restricted representation is simpler to understand...
to K. The corresponding double coset structure carries information about how the resulting representation decomposes.
They are also important in functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
, where in some important cases functions left-invariant and right-invariant by a subgroup K can form a commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
under convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
: see Gelfand pair
Gelfand pair
In mathematics, the expression Gelfand pair is a pair consisting of a group G and a subgroup K that satisfies a certain property on restricted representations. The theory of Gelfand pairs is closely related to the topic of spherical functions in the classical theory of special functions, and to...
.
In geometry, a Clifford–Klein form is a double coset space Γ\G/H, where G is a reductive Lie group, H is a closed subgroup, and Γ is a discrete subgroup (of G) that acts properly discontinuously on the homogeneous space
Homogeneous space
In mathematics, particularly in the theories of Lie groups, algebraic groups and topological groups, a homogeneous space for a group G is a non-empty manifold or topological space X on which G acts continuously by symmetry in a transitive way. A special case of this is when the topological group,...
G/H.
In number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, the Hecke algebra
Hecke operator
In mathematics, in particular in the theory of modular forms, a Hecke operator, studied by , is a certain kind of "averaging" operator that plays a significant role in the structure of vector spaces of modular forms and more general automorphic representations....
corresponding to a congruence subgroup
Congruence subgroup
In mathematics, a congruence subgroup of a matrix group with integer entries is a subgroup defined by congruence conditions on the entries. A very simple example would be invertible 2x2 integer matrices of determinant 1, such that the off-diagonal entries are even.An importance class of congruence...
Γ of the modular group
Modular group
In mathematics, the modular group Γ is a fundamental object of study in number theory, geometry, algebra, and many other areas of advanced mathematics...
is spanned by elements of the double coset space
; the algebra structure is that acquired from the multiplication of double cosets described above. Of particular importance are the Hecke operators corresponding to the double cosets 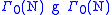or 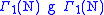, where 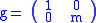(these have different properties depending on whether m and N are coprime or not), and the diamond operators 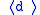given by the double cosets 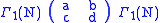where and we require 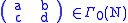(the choice of a, b, c does not affect the answer).