Great circle
Encyclopedia
A great circle, also known as a Riemannian circle
, of a sphere
is the intersection of the sphere and a plane which passes through the center point of the sphere, as opposed to a general circle of a sphere where the plane is not required to pass through the center. (A small circle is the intersection of the sphere and a plane which does not pass through the center.) Any diameter
of any great circle coincides with a diameter of the sphere, and therefore all great circles have the same circumference
as each other, and have the same center as the sphere. A great circle is the largest circle that can be drawn on any given sphere. Every circle
in Euclidean space
is a great circle of exactly one sphere.
For any two points on the surface of a sphere there is a great circle through the two points. The minor arc of a great circle between two points is the shortest surface-path between them. In this sense the minor arc is analogous to “straight lines” in spherical geometry
. The length of the minor arc of a great circle is taken as the distance between two points on a surface of a sphere, namely the great-circle distance
. The great circles are the geodesic
s of the sphere.
In higher dimensions, the great circles on the n-sphere are the intersection of the n-sphere with two-planes that pass through the origin in the Euclidean space Rn+1.
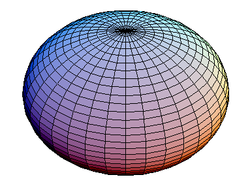Strictly speaking the Earth is not a perfect sphere
(it is an oblate spheroid or ellipsoid – i.e., slightly compressed at the poles), which means that the shortest distance between two points (a geodesic) is not quite a great circle. The equatorial radius of the earth is about 6378.137 kilometers. The polar radius of the earth is about 6356.752 kilometers (about 21.4 kilometers less). Nevertheless, the sphere model can be considered a first approximation.
When long distance aviation or nautical routes are drawn on a flat map (for instance, the Mercator projection
), they often look curved. This is because they lie on great circles. A route that would appear as a straight line on the map would actually be longer. An exception is the gnomonic projection
, in which all straight lines represent great circles.
On a spherical Earth, the meridians
(or lines of longitude) are great circles, as is the equator
. Lines of latitude
are not great circles, because they are smaller than the equator; their centers are not at the center of the Earth -- they are small circle
s instead. Since Earth is not a perfect sphere, the equator (which is generally considered a spherical great circle) is about 40,075 km, while a north-south meridian line (which is an ellipse) is almost 40,008 km. The quadratic mean or root mean square
of these extremes provides a decent approximation of the average great-circle circumference, about 40041.5 km.
Some examples of great circles on the celestial sphere
include the celestial horizon
, the celestial equator
, and the ecliptic
.
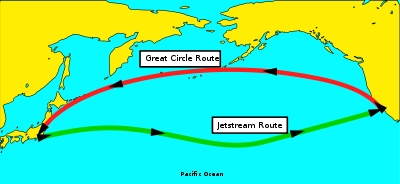
Great circle routes are used by ships and aircraft where currents and winds are not a significant factor. Flight length
s can therefore often be approximated to the great-circle distance
between two airports. For aircraft travelling west between continents in the northern hemisphere these paths will extend northward near or into the Arctic
region, however easterly flights will often fly a more southerly track to take advantage of the jet stream
.
For navigational convenience, Great Circle routes are often broken into a series of shorter rhumb line
s which allow the use of constant headings between waypoint
s along the Great Circle.
To prove that the minor arc of great circle is the shortest path connecting two points on the surface of a sphere, one has to apply calculus of variations
to it.
Consider the class of all regular paths from a point p to another point q. Introduce spherical coordinates so that p coincides with the north pole. Any curve on the sphere that does not intersect either pole, except possibly at the endpoints, can be parametrized by
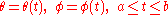
provided we allow φ to take on arbitrary real values. The infinitesimal arc length in these coordinates is
Riemannian circle
In metric space theory and Riemannian geometry, the Riemannian circle is a great circle equipped with its great-circle distance...
, of a sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
is the intersection of the sphere and a plane which passes through the center point of the sphere, as opposed to a general circle of a sphere where the plane is not required to pass through the center. (A small circle is the intersection of the sphere and a plane which does not pass through the center.) Any diameter
Diameter
In geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints are on the circle. The diameters are the longest chords of the circle...
of any great circle coincides with a diameter of the sphere, and therefore all great circles have the same circumference
Circumference
The circumference is the distance around a closed curve. Circumference is a special perimeter.-Circumference of a circle:The circumference of a circle is the length around it....
as each other, and have the same center as the sphere. A great circle is the largest circle that can be drawn on any given sphere. Every circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
in Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
is a great circle of exactly one sphere.
For any two points on the surface of a sphere there is a great circle through the two points. The minor arc of a great circle between two points is the shortest surface-path between them. In this sense the minor arc is analogous to “straight lines” in spherical geometry
Spherical geometry
Spherical geometry is the geometry of the two-dimensional surface of a sphere. It is an example of a geometry which is not Euclidean. Two practical applications of the principles of spherical geometry are to navigation and astronomy....
. The length of the minor arc of a great circle is taken as the distance between two points on a surface of a sphere, namely the great-circle distance
Great-circle distance
The great-circle distance or orthodromic distance is the shortest distance between any two points on the surface of a sphere measured along a path on the surface of the sphere . Because spherical geometry is rather different from ordinary Euclidean geometry, the equations for distance take on a...
. The great circles are the geodesic
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
s of the sphere.
In higher dimensions, the great circles on the n-sphere are the intersection of the n-sphere with two-planes that pass through the origin in the Euclidean space Rn+1.
Earth geodesics
Reference ellipsoid
In geodesy, a reference ellipsoid is a mathematically-defined surface that approximates the geoid, the truer figure of the Earth, or other planetary body....
(it is an oblate spheroid or ellipsoid – i.e., slightly compressed at the poles), which means that the shortest distance between two points (a geodesic) is not quite a great circle. The equatorial radius of the earth is about 6378.137 kilometers. The polar radius of the earth is about 6356.752 kilometers (about 21.4 kilometers less). Nevertheless, the sphere model can be considered a first approximation.
When long distance aviation or nautical routes are drawn on a flat map (for instance, the Mercator projection
Mercator projection
The Mercator projection is a cylindrical map projection presented by the Belgian geographer and cartographer Gerardus Mercator, in 1569. It became the standard map projection for nautical purposes because of its ability to represent lines of constant course, known as rhumb lines or loxodromes, as...
), they often look curved. This is because they lie on great circles. A route that would appear as a straight line on the map would actually be longer. An exception is the gnomonic projection
Gnomonic projection
A gnomonic map projection displays all great circles as straight lines. Thus the shortest route between two locations in reality corresponds to that on the map. This is achieved by projecting, with respect to the center of the Earth , the Earth's surface onto a tangent plane. The least distortion...
, in which all straight lines represent great circles.
On a spherical Earth, the meridians
Meridian (geography)
A meridian is an imaginary line on the Earth's surface from the North Pole to the South Pole that connects all locations along it with a given longitude. The position of a point along the meridian is given by its latitude. Each meridian is perpendicular to all circles of latitude...
(or lines of longitude) are great circles, as is the equator
Equator
An equator is the intersection of a sphere's surface with the plane perpendicular to the sphere's axis of rotation and containing the sphere's center of mass....
. Lines of latitude
Latitude
In geography, the latitude of a location on the Earth is the angular distance of that location south or north of the Equator. The latitude is an angle, and is usually measured in degrees . The equator has a latitude of 0°, the North pole has a latitude of 90° north , and the South pole has a...
are not great circles, because they are smaller than the equator; their centers are not at the center of the Earth -- they are small circle
Small circle
A circle of a sphere is a circle defined as the intersection of a sphere and a plane. If the plane contains the center of the sphere then the circle is called a great circle, otherwise it is a small circle...
s instead. Since Earth is not a perfect sphere, the equator (which is generally considered a spherical great circle) is about 40,075 km, while a north-south meridian line (which is an ellipse) is almost 40,008 km. The quadratic mean or root mean square
Root mean square
In mathematics, the root mean square , also known as the quadratic mean, is a statistical measure of the magnitude of a varying quantity. It is especially useful when variates are positive and negative, e.g., sinusoids...
of these extremes provides a decent approximation of the average great-circle circumference, about 40041.5 km.
Some examples of great circles on the celestial sphere
Celestial sphere
In astronomy and navigation, the celestial sphere is an imaginary sphere of arbitrarily large radius, concentric with the Earth and rotating upon the same axis. All objects in the sky can be thought of as projected upon the celestial sphere. Projected upward from Earth's equator and poles are the...
include the celestial horizon
Celestial horizon
The celestial horizon, also called the rational horizon, is a great circle parallel to the horizon, in which a plane at right angles to Zenith and Nadir lines are passing through the centre of the earth and intersects the celestial sphere, the center of which is the center of the Earth....
, the celestial equator
Celestial equator
The celestial equator is a great circle on the imaginary celestial sphere, in the same plane as the Earth's equator. In other words, it is a projection of the terrestrial equator out into space...
, and the ecliptic
Ecliptic
The ecliptic is the plane of the earth's orbit around the sun. In more accurate terms, it is the intersection of the celestial sphere with the ecliptic plane, which is the geometric plane containing the mean orbit of the Earth around the Sun...
.
Great circle routes are used by ships and aircraft where currents and winds are not a significant factor. Flight length
Flight length
In aviation, the flight length is defined as the time airborne during a flight.- Domestic :A short-haul domestic flight is commonly categorized into being no longer than 1.5 hours in length, meaning that all domestic flights within a country such as the United Kingdom are short-haul...
s can therefore often be approximated to the great-circle distance
Great-circle distance
The great-circle distance or orthodromic distance is the shortest distance between any two points on the surface of a sphere measured along a path on the surface of the sphere . Because spherical geometry is rather different from ordinary Euclidean geometry, the equations for distance take on a...
between two airports. For aircraft travelling west between continents in the northern hemisphere these paths will extend northward near or into the Arctic
Arctic
The Arctic is a region located at the northern-most part of the Earth. The Arctic consists of the Arctic Ocean and parts of Canada, Russia, Greenland, the United States, Norway, Sweden, Finland, and Iceland. The Arctic region consists of a vast, ice-covered ocean, surrounded by treeless permafrost...
region, however easterly flights will often fly a more southerly track to take advantage of the jet stream
Jet stream
Jet streams are fast flowing, narrow air currents found in the atmospheres of some planets, including Earth. The main jet streams are located near the tropopause, the transition between the troposphere and the stratosphere . The major jet streams on Earth are westerly winds...
.
For navigational convenience, Great Circle routes are often broken into a series of shorter rhumb line
Rhumb line
In navigation, a rhumb line is a line crossing all meridians of longitude at the same angle, i.e. a path derived from a defined initial bearing...
s which allow the use of constant headings between waypoint
Waypoint
A waypoint is a reference point in physical space used for purposes of navigation.-Concept:Waypoints are sets of coordinates that identify a point in physical space. Coordinates used can vary depending on the application. For terrestrial navigation these coordinates can include longitude and...
s along the Great Circle.
Derivation of shortest paths
Calculus of variations
Calculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
to it.
Consider the class of all regular paths from a point p to another point q. Introduce spherical coordinates so that p coincides with the north pole. Any curve on the sphere that does not intersect either pole, except possibly at the endpoints, can be parametrized by
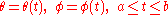
provided we allow φ to take on arbitrary real values. The infinitesimal arc length in these coordinates is
-
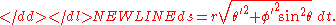
So the length of a curve γ from p to q is a functionalFunctional (mathematics)In mathematics, and particularly in functional analysis, a functional is a map from a vector space into its underlying scalar field. In other words, it is a function that takes a vector as its input argument, and returns a scalar...
of the curve given by
-
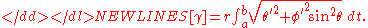
Note that S[γ] does not exceed the length of the meridian from p to q:
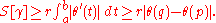
Since the starting point and ending point are fixed, S is minimized if and only if φ' = 0, so the curve must lie on a meridian of the sphere φ = φ0 = constant. In Cartesian coordinates, this is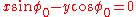
which is a plane through the origin, i.e., the center of the sphere.
External links
- Great Circle – from MathWorld Great Circle description, figures, and equations. Mathworld, Wolfram Research, Inc. c1999
- Great Circle Mapper Interactive tool for plotting great circle routes.
- Blue Marble Mapper Draws Great Circle routes between airports using the NASA Blue Marble as the base map.
- Air Route Calculator and Maps See Great Circle routes between most airports using Google Maps. See closest and furthest airports from origin and destination.
- Great Circle Calculator deriving (initial) course and distance between two points.
- Great Circle Distance Graphical tool for drawing great circles over maps. Also shows distance and azimuth in a table.
- Great Circles on Mercator's Chart by John Snyder with additional contributions by Jeff Bryant, Pratik Desai, and Carl Woll, Wolfram Demonstrations ProjectWolfram Demonstrations ProjectThe Wolfram Demonstrations Project is hosted by Wolfram Research, whose stated goal is to bring computational exploration to the widest possible audience. It consists of an organized, open-source collection of small interactive programs called Demonstrations, which are meant to visually and...
. - 3D First Problem 3D javascript interactive tool (Google ChromeGoogle ChromeGoogle Chrome is a web browser developed by Google that uses the WebKit layout engine. It was first released as a beta version for Microsoft Windows on September 2, 2008, and the public stable release was on December 11, 2008. The name is derived from the graphical user interface frame, or...
, Firefox, Safari (web browser)Safari (web browser)Safari is a web browser developed by Apple Inc. and included with the Mac OS X and iOS operating systems. First released as a public beta on January 7, 2003 on the company's Mac OS X operating system, it became Apple's default browser beginning with Mac OS X v10.3 "Panther". Safari is also the...
). - 3D Second Problem 3D javascript interactive tool (Google ChromeGoogle ChromeGoogle Chrome is a web browser developed by Google that uses the WebKit layout engine. It was first released as a beta version for Microsoft Windows on September 2, 2008, and the public stable release was on December 11, 2008. The name is derived from the graphical user interface frame, or...
, Firefox, Safari (web browser)Safari (web browser)Safari is a web browser developed by Apple Inc. and included with the Mac OS X and iOS operating systems. First released as a public beta on January 7, 2003 on the company's Mac OS X operating system, it became Apple's default browser beginning with Mac OS X v10.3 "Panther". Safari is also the...
).
-