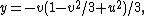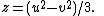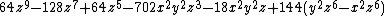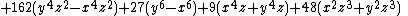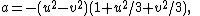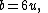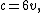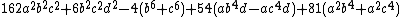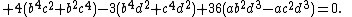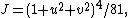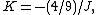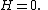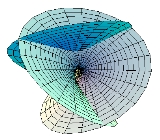
Enneper surface
Encyclopedia
In mathematics
, in the fields of differential geometry and algebraic geometry
, the Enneper surface is a surface that can be described parametrically by:
It was introduced by Alfred Enneper
in connection with minimal surface
theory.
Implicitization methods of algebraic geometry
can be used to find out that the points in the Enneper surface given above satisfy the degree-9 polynomial
equation
Dually, the tangent plane at the point with given parameters is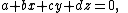 where
where
Its coefficients satisfy the implicit degree-6 polynomial equation
Enneper's is a minimal surface
. The Jacobian
, Gaussian curvature
and mean curvature
are
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in the fields of differential geometry and algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, the Enneper surface is a surface that can be described parametrically by:
It was introduced by Alfred Enneper
Alfred Enneper
Alfred Enneper earned his PhD from the Georg-August-Universität Göttingen in 1856 for his dissertation about functions with complex arguments. After his habilitation 1859 in Göttingen he was from 1870 on Professor at Göttingen. He studied minimal surfaces and parametrized Enneper's minimal...
in connection with minimal surface
Minimal surface
In mathematics, a minimal surface is a surface with a mean curvature of zero.These include, but are not limited to, surfaces of minimum area subject to various constraints....
theory.

-
-
-
-
- Figure 1. An Enneper surface
-
-
-
-
Implicitization methods of algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
can be used to find out that the points in the Enneper surface given above satisfy the degree-9 polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
equation
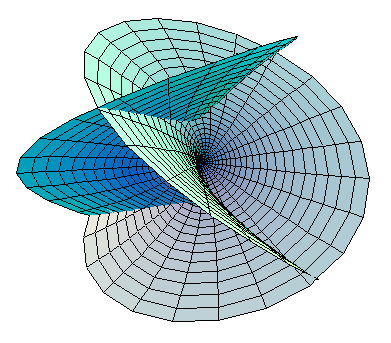
- Figure 2. The Enneper surface in Figure 1 has been rotated 30° around the +z axis.
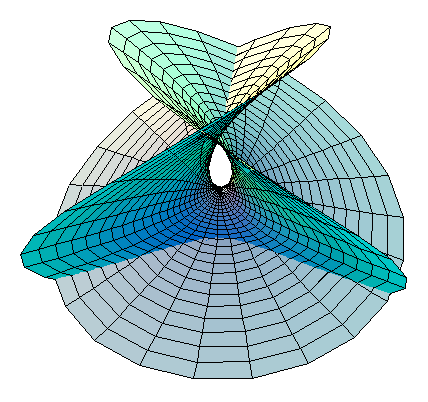
- Figure 3. The Enneper surface in Figure 1 has been rotated 60° around the +z axis.
Dually, the tangent plane at the point with given parameters is
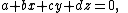 where
where
Its coefficients satisfy the implicit degree-6 polynomial equation
Enneper's is a minimal surface
Minimal surface
In mathematics, a minimal surface is a surface with a mean curvature of zero.These include, but are not limited to, surfaces of minimum area subject to various constraints....
. The Jacobian
Jacobian
In vector calculus, the Jacobian matrix is the matrix of all first-order partial derivatives of a vector- or scalar-valued function with respect to another vector. Suppose F : Rn → Rm is a function from Euclidean n-space to Euclidean m-space...
, Gaussian curvature
Gaussian curvature
In differential geometry, the Gaussian curvature or Gauss curvature of a point on a surface is the product of the principal curvatures, κ1 and κ2, of the given point. It is an intrinsic measure of curvature, i.e., its value depends only on how distances are measured on the surface, not on the way...
and mean curvature
Mean curvature
In mathematics, the mean curvature H of a surface S is an extrinsic measure of curvature that comes from differential geometry and that locally describes the curvature of an embedded surface in some ambient space such as Euclidean space....
are