Triangulation (topology)
Encyclopedia
In mathematics
, topology
generalizes the notion of triangulation in a natural way as follows:
A triangulation of a topological space
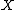is a simplicial complex
K, homeomorphic to X, together with a homeomorphism
h:K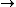
X.
Triangulation is useful in determining the properties of a topological space. For example, one can compute homology
and cohomology
groups of a triangulated space using simplicial homology and cohomology theories instead of more complicated homology and cohomology theories.
s, there is a slightly stronger notion of triangulation: a piecewise-linear triangulation (sometimes just called a triangulation) is a triangulation with the extra property that the link of any simplex is a piecewise-linear sphere. The link of a simplex s in a simplicial complex K is a subcomplex of K consisting of the simplices t that are disjoint from s and such that both s and t are faces of some higher-dimensional simplex in K. For instance, in a two-dimensional piecewise-linear manifold formed by a set of vertices, edges, and triangles, the link of a vertex s consists of the cycle
of vertices and edges surrounding s: if t is a vertex in this cycle, it and s are both endpoints of an edge of K, and if t is an edge in this cycle, it and s are both faces of a triangle of K. This cycle is homeomorphic to a circle, which is a 1-dimensional sphere.
For manifolds of dimension at most 4 this extra property automatically holds: in any simplicial complex homeomorphic to a manifold, the link of any simplex can only be homeomorphic to a sphere. But in dimension n ≥ 5 the (n − 3)-fold suspension of the Poincaré sphere
is a topological manifold (homeomorphic to the n-sphere) with a triangulation that is not piecewise-linear: it has a simplex whose link is the Poincaré homology sphere, a three-dimensional manifold that is not homeomorphic to a sphere.
The question of which manifolds have piecewise-linear triangulations has led to much research in topology.
Differentiable manifold
s (Stewart Cairns, , L.E.J. Brouwer
, Hans Freudenthal
) and subanalytic set
s (Heisuke Hironaka
and Robert Hardt) admit a piecewise-linear triangulation.
Topological manifold
s of dimensions 2 and 3 are always triangulable by an essentially unique triangulation
(up to piecewise-linear equivalence); this was proved for surface
s by Tibor Radó
in the 1920s and for three-manifolds by Edwin E. Moise
and R. H. Bing in the 1950s, with later simplifications by Peter Shalen
. As shown independently by James Munkres
, Steve Smale and
, each of these manifolds admits
a smooth structure
, unique up to diffeomorphism
(see ).
In dimension 4, however, the E8 manifold
does not admit a triangulation, and some compact 4-manifolds have an infinite number of triangulations, all piecewise-linear inequivalent. In dimension greater than 4, the question of whether all topological manifolds have triangulations is an open problem, though it is known that some do not have piecewise-linear
triangulations (see Hauptvermutung
).
. There is a standard proof that smooth closed surfaces can be triangulated (see Jost 1997). Indeed, if the surface is given a Riemannian metric, each point x is contained inside a small convex geodesic
triangle lying inside a normal ball with centre x. The interiors of finitely many of the triangles will cover
the surface; since edges of different triangles either coincide or intersect transversally, this finite set of triangles can be used iteratively to construct a triangulation.
Another simple procedure for triangulating differentiable manifolds was given by Hassler Whitney
in 1957, based on his embedding theorem. In fact, if X is a closed n-submanifold
of Rm, subdivide a cubical lattice in Rm into simplices to give a triangulation of Rm. By taking the mesh of the lattice small enough and slightly moving finitely many of the vertices, the triangulation will be in general position with respect to X: thus no simplices of dimension < s=m-n
intersect X and each s-simplex intersecting X
These points of intersection and their barycentres (corresponding to higher dimensional simplices intersecting X) generate an n-dimensional simplicial subcomplex in Rm, lying wholly inside the tubular neighbourhood. The triangulation is given by the projection of this simplicial complex onto X.
is an embedding of a graph onto the surface in such a way that the faces of the embedding are exactly the cliques of the graph (Hartsfeld and Gerhard Ringel
1981; Larrión et al. 2002; Malnič and Mohar 1992). Equivalently, every face is a triangle, every triangle is a face, and the graph is not itself a clique. The clique complex
of the graph is then homeomorphic to the surface. The 1-skeletons of Whitney triangulations are exactly the locally cyclic graphs
other than K4.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
generalizes the notion of triangulation in a natural way as follows:
A triangulation of a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
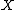is a simplicial complexSimplicial complex
In mathematics, a simplicial complex is a topological space of a certain kind, constructed by "gluing together" points, line segments, triangles, and their n-dimensional counterparts...
K, homeomorphic to X, together with a homeomorphism
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
h:K
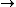X.Triangulation is useful in determining the properties of a topological space. For example, one can compute homology
Homology (mathematics)
In mathematics , homology is a certain general procedure to associate a sequence of abelian groups or modules with a given mathematical object such as a topological space or a group...
and cohomology
Cohomology
In mathematics, specifically in algebraic topology, cohomology is a general term for a sequence of abelian groups defined from a co-chain complex. That is, cohomology is defined as the abstract study of cochains, cocycles, and coboundaries...
groups of a triangulated space using simplicial homology and cohomology theories instead of more complicated homology and cohomology theories.
Piecewise linear structures
For topological manifoldManifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
s, there is a slightly stronger notion of triangulation: a piecewise-linear triangulation (sometimes just called a triangulation) is a triangulation with the extra property that the link of any simplex is a piecewise-linear sphere. The link of a simplex s in a simplicial complex K is a subcomplex of K consisting of the simplices t that are disjoint from s and such that both s and t are faces of some higher-dimensional simplex in K. For instance, in a two-dimensional piecewise-linear manifold formed by a set of vertices, edges, and triangles, the link of a vertex s consists of the cycle
Cycle graph
In graph theory, a cycle graph or circular graph is a graph that consists of a single cycle, or in other words, some number of vertices connected in a closed chain. The cycle graph with n vertices is called Cn...
of vertices and edges surrounding s: if t is a vertex in this cycle, it and s are both endpoints of an edge of K, and if t is an edge in this cycle, it and s are both faces of a triangle of K. This cycle is homeomorphic to a circle, which is a 1-dimensional sphere.
For manifolds of dimension at most 4 this extra property automatically holds: in any simplicial complex homeomorphic to a manifold, the link of any simplex can only be homeomorphic to a sphere. But in dimension n ≥ 5 the (n − 3)-fold suspension of the Poincaré sphere
Poincaré sphere
Poincaré sphere, often spelled Poincare sphere may refer to:* Poincaré sphere, in optics, is a graphical tool for visualizing different types of polarized light...
is a topological manifold (homeomorphic to the n-sphere) with a triangulation that is not piecewise-linear: it has a simplex whose link is the Poincaré homology sphere, a three-dimensional manifold that is not homeomorphic to a sphere.
The question of which manifolds have piecewise-linear triangulations has led to much research in topology.
Differentiable manifold
Differentiable manifold
A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
s (Stewart Cairns, , L.E.J. Brouwer
Luitzen Egbertus Jan Brouwer
Luitzen Egbertus Jan Brouwer FRS , usually cited as L. E. J. Brouwer but known to his friends as Bertus, was a Dutch mathematician and philosopher, a graduate of the University of Amsterdam, who worked in topology, set theory, measure theory and complex analysis.-Biography:Early in his career,...
, Hans Freudenthal
Hans Freudenthal
Hans Freudenthal was a Dutch mathematician. He made substantial contributions to algebraic topology and also took an interest in literature, philosophy, history and mathematics education....
) and subanalytic set
Subanalytic set
In mathematics, particularly in the subfield of real analytic geometry, a subanalytic set is a set of points defined in a way broader than for semianalytic sets...
s (Heisuke Hironaka
Heisuke Hironaka
is a Japanese mathematician. After completing his undergraduate studies at Kyoto University, he received his Ph.D. from Harvard while under the direction of Oscar Zariski. He won the Fields Medal in 1970....
and Robert Hardt) admit a piecewise-linear triangulation.
Topological manifold
Topological manifold
In mathematics, a topological manifold is a topological space which looks locally like Euclidean space in a sense defined below...
s of dimensions 2 and 3 are always triangulable by an essentially unique triangulation
Hauptvermutung
The Hauptvermutung of geometric topology is the conjecture that any two triangulations of a triangulable space have a common refinement, a single triangulation that is a subdivision of both of them. It was originally formulated in 1908, by Steinitz and Tietze.This conjecture is now known to be false...
(up to piecewise-linear equivalence); this was proved for surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
s by Tibor Radó
Tibor Radó
Tibor Radó was a Hungarian mathematician who moved to the USA after World War I. He was born in Budapest and between 1913 and 1915 attended the Polytechnic Institute. In World War I, he became a First Lieutenant in the Hungarian Army and was captured on the Russian Front...
in the 1920s and for three-manifolds by Edwin E. Moise
Edwin E. Moise
Edwin Evariste Moise was an American mathematician and mathematics education reformer. After his retirement from mathematics he became a literary critic of 19th century English poetry and had several notes published in that field.-Early life and education:...
and R. H. Bing in the 1950s, with later simplifications by Peter Shalen
Peter Shalen
Peter B. Shalen is an American mathematician, working primarily in low-dimensional topology. He is the "S" in JSJ decomposition.-Life:He graduated from Stuyvesant High School in 1962, and went on to earn a B.A. from Harvard College in 1966 and his Ph.D. from Harvard University in 1972...
. As shown independently by James Munkres
James Munkres
James Raymond Munkres is a Professor Emeritus of mathematics at MIT and the author of several texts in the area of topology, including Topology , Analysis on Manifolds, Elements of Algebraic Topology, and Elementary Differential Topology...
, Steve Smale and
, each of these manifolds admits
a smooth structure
Smooth structure
In mathematics, a smooth structure on a manifold allows for an unambiguous notion of smooth function. In particular, a smooth structure allows one to perform mathematical analysis on the manifold....
, unique up to diffeomorphism
Diffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
(see ).
In dimension 4, however, the E8 manifold
E8 manifold
In mathematics, the E8 manifold is the unique compact, simply connected topological 4-manifold with intersection form the E8 lattice.The E8 manifold was discovered by Michael Freedman in 1982...
does not admit a triangulation, and some compact 4-manifolds have an infinite number of triangulations, all piecewise-linear inequivalent. In dimension greater than 4, the question of whether all topological manifolds have triangulations is an open problem, though it is known that some do not have piecewise-linear
Piecewise linear manifold
In mathematics, a piecewise linear manifold is a topological manifold together with a piecewise linear structure on it. Such a structure can be defined by means of an atlas, such that one can pass from chart to chart in it by piecewise linear functions.An isomorphism of PL manifolds is called a PL...
triangulations (see Hauptvermutung
Hauptvermutung
The Hauptvermutung of geometric topology is the conjecture that any two triangulations of a triangulable space have a common refinement, a single triangulation that is a subdivision of both of them. It was originally formulated in 1908, by Steinitz and Tietze.This conjecture is now known to be false...
).
Explicit methods of triangulation
An important special case of topological triangulation is that of two-dimensional surfaces, or closed 2-manifoldsManifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
. There is a standard proof that smooth closed surfaces can be triangulated (see Jost 1997). Indeed, if the surface is given a Riemannian metric, each point x is contained inside a small convex geodesic
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
triangle lying inside a normal ball with centre x. The interiors of finitely many of the triangles will cover
the surface; since edges of different triangles either coincide or intersect transversally, this finite set of triangles can be used iteratively to construct a triangulation.
Another simple procedure for triangulating differentiable manifolds was given by Hassler Whitney
Hassler Whitney
Hassler Whitney was an American mathematician. He was one of the founders of singularity theory, and did foundational work in manifolds, embeddings, immersions, and characteristic classes.-Work:...
in 1957, based on his embedding theorem. In fact, if X is a closed n-submanifold
Submanifold
In mathematics, a submanifold of a manifold M is a subset S which itself has the structure of a manifold, and for which the inclusion map S → M satisfies certain properties. There are different types of submanifolds depending on exactly which properties are required...
of Rm, subdivide a cubical lattice in Rm into simplices to give a triangulation of Rm. By taking the mesh of the lattice small enough and slightly moving finitely many of the vertices, the triangulation will be in general position with respect to X: thus no simplices of dimension < s=m-n
intersect X and each s-simplex intersecting X
- does so in exactly one interior point;
- makes a strictly positive angle with the tangent plane;
- lies wholly inside some tubular neighbourhood of X.
These points of intersection and their barycentres (corresponding to higher dimensional simplices intersecting X) generate an n-dimensional simplicial subcomplex in Rm, lying wholly inside the tubular neighbourhood. The triangulation is given by the projection of this simplicial complex onto X.
Graphs on surfaces
A Whitney triangulation or clean triangulation of a surfaceSurface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
is an embedding of a graph onto the surface in such a way that the faces of the embedding are exactly the cliques of the graph (Hartsfeld and Gerhard Ringel
Gerhard Ringel
Gerhard Ringel was a German mathematician who earned his Ph.D. from the University of Bonn in 1951...
1981; Larrión et al. 2002; Malnič and Mohar 1992). Equivalently, every face is a triangle, every triangle is a face, and the graph is not itself a clique. The clique complex
Clique complex
Clique complexes, flag complexes, and conformal hypergraphs are closely related mathematical objects in graph theory and geometric topology that each describe the cliques of an undirected graph.-Clique complex:...
of the graph is then homeomorphic to the surface. The 1-skeletons of Whitney triangulations are exactly the locally cyclic graphs
Neighbourhood (graph theory)
In graph theory, an adjacent vertex of a vertex v in a graph is a vertex that is connected to v by an edge. The neighbourhood of a vertex v in a graph G is the induced subgraph of G consisting of all vertices adjacent to v and all edges connecting two such vertices. For example, the image shows a...
other than K4.