Decimal representation
Encyclopedia
A decimal representation of a non-negative real number
r is an expression of the form of a series
, traditionally written as a sum
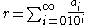
where a0 is a nonnegative integer, and a1, a2, … are integers satisfying 0 ≤ ai ≤ 9, called the digits of the decimal representation. The sequence of digits specified may be finite, in which case any further digits ai are assumed to be 0. Some authors forbid decimal representations with an infinite sequence of digits 9.
This restriction still allows a decimal representation for each non-negative real number, but additionally makes such a representation unique.
The number defined by a decimal representation is often written more briefly as
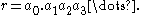
That is to say, a0 is the integer part of r, not necessarily between 0 and 9, and a1, a2, a3, … are the digits forming the fractional part of r.
Both notations above are, by definition, the following limit of a sequence
:
.
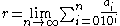s with finite decimal representations.
Assume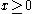
. Then for every integer 
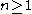there is a finite decimal 
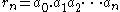such that
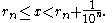
Proof:
Let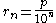
, where 
.
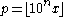Then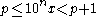
, and the result follows from dividing all sides by 
.
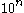(The fact that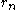
has a finite decimal representation is easily established.)
(where the infinite sequences of digits 0 and 9, respectively, are represented by "..."). Conventionally, the version with zero digits is preferred; by omitting the infinite sequence of zero digits, removing any final zero digits and a possible final decimal point, a normalized finite decimal representation is obtained.
Proof:
If the decimal expansion of x will end in zeros, or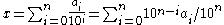
for some n,
then the denominator of x is of the form 10n = 2n5n.
Conversely, if the denominator of x is of the form 2n5m,
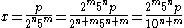
for some p.
While x is of the form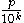
,
for some n.
By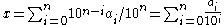
,
x will end in zeros.
Every time this happens the number is still a rational number
(i.e. can alternatively be represented as a ratio of a non-negative and a positive integer).
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
r is an expression of the form of a series
Series (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
, traditionally written as a sum
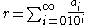
where a0 is a nonnegative integer, and a1, a2, … are integers satisfying 0 ≤ ai ≤ 9, called the digits of the decimal representation. The sequence of digits specified may be finite, in which case any further digits ai are assumed to be 0. Some authors forbid decimal representations with an infinite sequence of digits 9.
This restriction still allows a decimal representation for each non-negative real number, but additionally makes such a representation unique.
The number defined by a decimal representation is often written more briefly as
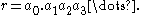
That is to say, a0 is the integer part of r, not necessarily between 0 and 9, and a1, a2, a3, … are the digits forming the fractional part of r.
Both notations above are, by definition, the following limit of a sequence
Limit of a sequence
The limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
:
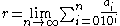.Finite decimal approximations
Any real number can be approximated to any desired degree of accuracy by rational numberRational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s with finite decimal representations.
Assume
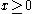. Then for every integer 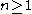there is a finite decimal 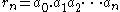such that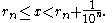Proof:
Let
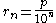, where 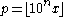.Then
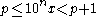, and the result follows from dividing all sides by 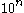.(The fact that
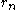has a finite decimal representation is easily established.)Non-uniqueness of decimal representation
Some real numbers have two infinite decimal representations. For example, the number 1 may be equally represented by 1.000... as by 0.999...0.999...
In mathematics, the repeating decimal 0.999... denotes a real number that can be shown to be the number one. In other words, the symbols 0.999... and 1 represent the same number...
(where the infinite sequences of digits 0 and 9, respectively, are represented by "..."). Conventionally, the version with zero digits is preferred; by omitting the infinite sequence of zero digits, removing any final zero digits and a possible final decimal point, a normalized finite decimal representation is obtained.
Finite decimal representations
The decimal expansion of non-negative real number x will end in zeros (or in nines) if, and only if, x is a rational number whose denominator is of the form 2n5m, where m and n are non-negative integers.Proof:
If the decimal expansion of x will end in zeros, or
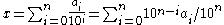
for some n,
then the denominator of x is of the form 10n = 2n5n.
Conversely, if the denominator of x is of the form 2n5m,
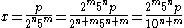
for some p.
While x is of the form
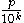, for some n.By
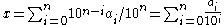,x will end in zeros.
Recurring decimal representations
Some real numbers have decimal expansions that eventually get into loops, endlessly repeating a sequence of one or more digits:- 1/3 = 0.33333...
- 1/7 = 0.142857142857...
- 1318/185 = 7.1243243243...
Every time this happens the number is still a rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
(i.e. can alternatively be represented as a ratio of a non-negative and a positive integer).
External links
- Plouffe's inverter tries to identify a number given the start of its decimal representation. For instance, given 3.14159265 it will say that your input probably came from one of the following and list πPi' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
as the simplest.