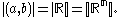Cardinality of the continuum
Encyclopedia
In set theory
, the cardinality of the continuum is the cardinality or “size” of the set of real numbers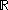 , sometimes called the continuum. It is an infinite cardinal number
, sometimes called the continuum. It is an infinite cardinal number
and is denoted by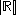 or
or  (a lowercase fraktur script c).
(a lowercase fraktur script c).
The real numbers are more numerous than the natural numbers
are more numerous than the natural numbers 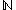 . Moreover,
. Moreover, 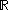 has the same number of elements as the power set of
has the same number of elements as the power set of 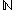 . Symbolically, if the cardinality of
. Symbolically, if the cardinality of 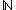 is denoted as
is denoted as 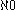 , the cardinality of the continuum is
, the cardinality of the continuum is
This was proven by Georg Cantor
in his 1874 uncountability proof
, part of his groundbreaking study of different infinities, and later more simply in his diagonal argument
. Cantor defined cardinality in terms of bijective functions: two sets have the same cardinality if and only if there exists a bijective function between them.
Between any two real numbers a < b, no matter how close they are to each other, there are always infinitely many other real numbers, and Cantor showed that they are as many as those contained in the whole set of real numbers. In other words, the open interval (a,b) is equinumerous with This is also true for several other infinite sets, such as any n-dimensional Euclidean space
This is also true for several other infinite sets, such as any n-dimensional Euclidean space
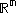 (see Space filling curve). That is,
(see Space filling curve). That is,
The smallest infinite cardinal number is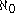 (aleph-naught). The second smallest is
(aleph-naught). The second smallest is 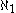 (aleph-one). The continuum hypothesis
(aleph-one). The continuum hypothesis
, which asserts that there are no sets whose cardinality is strictly between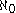 and
and  implies that
implies that 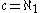 .
.
introduced the concept of cardinality to compare the sizes of infinite sets. He famously showed that the set of real numbers is uncountably infinite; i.e. is strictly greater than the cardinality of the natural numbers,
is strictly greater than the cardinality of the natural numbers, 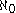 :
: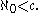
In other words, there are strictly more real numbers than there are integers. Cantor proved this statement in several different ways. See Cantor's first uncountability proof
and Cantor's diagonal argument
.
which states that the cardinality of any set is strictly less than that of its power set, i.e. |A| < 2|A|, and so the power set P(N) of the natural number
s N is uncountable. In fact, it can be shown that the cardinality of P(N) is equal to :
:
By the Cantor–Bernstein–Schroeder theorem
we conclude that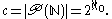
(A different proof of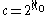 is given in Cantor's diagonal argument. This proof constructs a bijection from {0,1}N to R.)
is given in Cantor's diagonal argument. This proof constructs a bijection from {0,1}N to R.)
The cardinal equality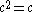 can be demonstrated using cardinal arithmetic:
can be demonstrated using cardinal arithmetic: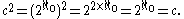
This argument is a condensed version of the notion of interleaving two binary sequences: let 0.a0a1a2... be the binary expansion of x and let 0.b0b1b2... be the binary expansion of y. Then z = 0.a0b0a1b1a2b2..., the interleaving of the binary expansions, is a well-defined function when x and y have unique binary expansions. Only countably many reals have non-unique binary expansions.
By using the rules of cardinal arithmetic one can also show that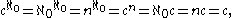
where n is any finite cardinal ≥ 2, and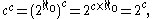
where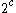 is the cardinality of the power set of R, and
is the cardinality of the power set of R, and 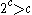 .
.
Alternative explanation for
Every real number has an infinite decimal expansion. For example,
(This is true even when the expansion repeats as in the first two examples.)
In any given case, the number of digits is countable
since they can be put into a one-to-one correspondence with the set of natural numbers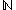 . This fact makes it sensible to talk about (for example) the first, the one-hundredth, or the millionth digit of
. This fact makes it sensible to talk about (for example) the first, the one-hundredth, or the millionth digit of  . Since the natural numbers have cardinality
. Since the natural numbers have cardinality 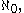 each real number has
each real number has 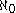 digits in its expansion.
digits in its expansion.
Since each real number can be broken into an integer part and a decimal fraction, we get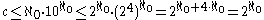
since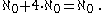
On the other hand, if we map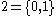 to
to 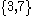 and consider that decimal fractions containing only 3 or 7 are only a part of the real numbers, then we get
and consider that decimal fractions containing only 3 or 7 are only a part of the real numbers, then we get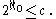
and thus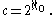
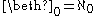 and
and 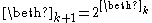 . So
. So  is the second beth number, beth-one:
is the second beth number, beth-one:
The third beth number, beth-two, is the cardinality of the power set of R (i.e. the set of all subsets of the real line
):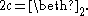
 is also the second aleph number
is also the second aleph number
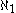 . In other words, the continuum hypothesis states that there is no set
. In other words, the continuum hypothesis states that there is no set 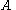 whose cardinality lies strictly between
whose cardinality lies strictly between 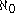 and
and 
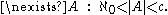
This statement is now known to be independent of the axioms of Zermelo–Fraenkel set theory
with the axiom of choice (ZFC). That is, both the hypothesis and its negation are consistent with these axioms. In fact, for every nonzero natural number
n, the equality =
= 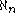 is independent of ZFC. (The case
is independent of ZFC. (The case 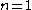 is the continuum hypothesis.) The same is true for most other alephs, although in some cases equality can be ruled out by König's theorem
is the continuum hypothesis.) The same is true for most other alephs, although in some cases equality can be ruled out by König's theorem
on the grounds of cofinality
, e.g.,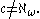 In particular,
In particular,  could be either
could be either 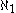 or
or 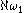 , where
, where 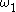 is the first uncountable ordinal
is the first uncountable ordinal
, so it could be either a successor cardinal
or a limit cardinal
, and either a regular cardinal
or a singular cardinal.
 . Some common examples are the following:
. Some common examples are the following:
 include:
include:
They all have cardinality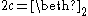 (Beth two).
(Beth two).
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
, the cardinality of the continuum is the cardinality or “size” of the set of real numbers
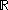 , sometimes called the continuum. It is an infinite cardinal number
, sometimes called the continuum. It is an infinite cardinal numberCardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
and is denoted by
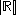 or
or  (a lowercase fraktur script c).
(a lowercase fraktur script c).The real numbers
 are more numerous than the natural numbers
are more numerous than the natural numbers 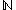 . Moreover,
. Moreover, 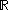 has the same number of elements as the power set of
has the same number of elements as the power set of 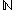 . Symbolically, if the cardinality of
. Symbolically, if the cardinality of 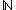 is denoted as
is denoted as 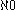 , the cardinality of the continuum is
, the cardinality of the continuum is
This was proven by Georg Cantor
Georg Cantor
Georg Ferdinand Ludwig Philipp Cantor was a German mathematician, best known as the inventor of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets,...
in his 1874 uncountability proof
Cantor's first uncountability proof
Georg Cantor's first uncountability proof demonstrates that the set of all real numbers is uncountable. This proof differs from the more familiar proof that uses his diagonal argument...
, part of his groundbreaking study of different infinities, and later more simply in his diagonal argument
Cantor's diagonal argument
Cantor's diagonal argument, also called the diagonalisation argument, the diagonal slash argument or the diagonal method, was published in 1891 by Georg Cantor as a mathematical proof that there are infinite sets which cannot be put into one-to-one correspondence with the infinite set of natural...
. Cantor defined cardinality in terms of bijective functions: two sets have the same cardinality if and only if there exists a bijective function between them.
Between any two real numbers a < b, no matter how close they are to each other, there are always infinitely many other real numbers, and Cantor showed that they are as many as those contained in the whole set of real numbers. In other words, the open interval (a,b) is equinumerous with
 This is also true for several other infinite sets, such as any n-dimensional Euclidean space
This is also true for several other infinite sets, such as any n-dimensional Euclidean spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
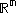 (see Space filling curve). That is,
(see Space filling curve). That is,
The smallest infinite cardinal number is
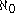 (aleph-naught). The second smallest is
(aleph-naught). The second smallest is 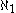 (aleph-one). The continuum hypothesis
(aleph-one). The continuum hypothesisContinuum hypothesis
In mathematics, the continuum hypothesis is a hypothesis, advanced by Georg Cantor in 1874, about the possible sizes of infinite sets. It states:Establishing the truth or falsehood of the continuum hypothesis is the first of Hilbert's 23 problems presented in the year 1900...
, which asserts that there are no sets whose cardinality is strictly between
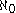 and
and  implies that
implies that 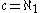 .
.Uncountability
Georg CantorGeorg Cantor
Georg Ferdinand Ludwig Philipp Cantor was a German mathematician, best known as the inventor of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets,...
introduced the concept of cardinality to compare the sizes of infinite sets. He famously showed that the set of real numbers is uncountably infinite; i.e.
 is strictly greater than the cardinality of the natural numbers,
is strictly greater than the cardinality of the natural numbers, 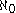 :
: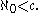
In other words, there are strictly more real numbers than there are integers. Cantor proved this statement in several different ways. See Cantor's first uncountability proof
Cantor's first uncountability proof
Georg Cantor's first uncountability proof demonstrates that the set of all real numbers is uncountable. This proof differs from the more familiar proof that uses his diagonal argument...
and Cantor's diagonal argument
Cantor's diagonal argument
Cantor's diagonal argument, also called the diagonalisation argument, the diagonal slash argument or the diagonal method, was published in 1891 by Georg Cantor as a mathematical proof that there are infinite sets which cannot be put into one-to-one correspondence with the infinite set of natural...
.
Cardinal equalities
A variation on Cantor's diagonal argument can be used to prove Cantor's theoremCantor's theorem
In elementary set theory, Cantor's theorem states that, for any set A, the set of all subsets of A has a strictly greater cardinality than A itself...
which states that the cardinality of any set is strictly less than that of its power set, i.e. |A| < 2|A|, and so the power set P(N) of the natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s N is uncountable. In fact, it can be shown that the cardinality of P(N) is equal to
 :
:
- Define a map f : R → P(Q) from the reals to the power set of the rationals by sending each real number x to the set
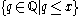 of all rationals less than or equal to x (with the reals viewed as Dedekind cutDedekind cutIn mathematics, a Dedekind cut, named after Richard Dedekind, is a partition of the rationals into two non-empty parts A and B, such that all elements of A are less than all elements of B, and A contains no greatest element....
of all rationals less than or equal to x (with the reals viewed as Dedekind cutDedekind cutIn mathematics, a Dedekind cut, named after Richard Dedekind, is a partition of the rationals into two non-empty parts A and B, such that all elements of A are less than all elements of B, and A contains no greatest element....
s, this is nothing other than the inclusion mapInclusion mapIn mathematics, if A is a subset of B, then the inclusion map is the function i that sends each element, x of A to x, treated as an element of B:i: A\rightarrow B, \qquad i=x....
in the set of sets of rationals). This map is injectiveInjective functionIn mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
since the rationals are denseDense setIn topology and related areas of mathematics, a subset A of a topological space X is called dense if any point x in X belongs to A or is a limit point of A...
in R. Since the rationals are countable we have that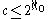 .
. - Let {0,2}N be the set of infinite sequenceSequenceIn mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
s with values in set {0,2}. This set clearly has cardinality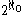 (the natural bijectionBijectionA bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
(the natural bijectionBijectionA bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
between the set of binary sequences and P(N) is given by the indicator function). Now associate to each such sequence (ai) the unique real number in the intervalUnit intervalIn mathematics, the unit interval is the closed interval , that is, the set of all real numbers that are greater than or equal to 0 and less than or equal to 1...
[0,1] with the ternaryTernary numeral systemTernary is the base- numeral system. Analogous to a bit, a ternary digit is a trit . One trit contains \log_2 3 bits of information...
-expansion given by the digits (ai), i.e. the i-th digit after the decimal point is ai. The image of this map is called the Cantor setCantor setIn mathematics, the Cantor set is a set of points lying on a single line segment that has a number of remarkable and deep properties. It was discovered in 1875 by Henry John Stephen Smith and introduced by German mathematician Georg Cantor in 1883....
. It is not hard to see that this map is injective, for by avoiding points with the digit 1 in their ternary expansion we avoid conflicts created by the fact that the ternary-expansion of a real number is not unique. We then have that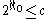 .
.
By the Cantor–Bernstein–Schroeder theorem
Cantor–Bernstein–Schroeder theorem
In set theory, the Cantor–Bernstein–Schroeder theorem, named after Georg Cantor, Felix Bernstein, and Ernst Schröder, states that, if there exist injective functions and between the sets A and B, then there exists a bijective function...
we conclude that
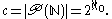
(A different proof of
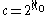 is given in Cantor's diagonal argument. This proof constructs a bijection from {0,1}N to R.)
is given in Cantor's diagonal argument. This proof constructs a bijection from {0,1}N to R.)The cardinal equality
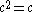 can be demonstrated using cardinal arithmetic:
can be demonstrated using cardinal arithmetic: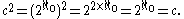
This argument is a condensed version of the notion of interleaving two binary sequences: let 0.a0a1a2... be the binary expansion of x and let 0.b0b1b2... be the binary expansion of y. Then z = 0.a0b0a1b1a2b2..., the interleaving of the binary expansions, is a well-defined function when x and y have unique binary expansions. Only countably many reals have non-unique binary expansions.
By using the rules of cardinal arithmetic one can also show that
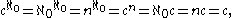
where n is any finite cardinal ≥ 2, and
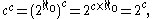
where
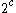 is the cardinality of the power set of R, and
is the cardinality of the power set of R, and 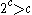 .
.Alternative explanation for 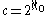
Every real number has an infinite decimal expansion. For example,
- 1/2 = 0.50000...
- 1/3 = 0.33333...
 = 3.14159....
= 3.14159....
(This is true even when the expansion repeats as in the first two examples.)
In any given case, the number of digits is countable
Countable set
In mathematics, a countable set is a set with the same cardinality as some subset of the set of natural numbers. A set that is not countable is called uncountable. The term was originated by Georg Cantor...
since they can be put into a one-to-one correspondence with the set of natural numbers
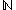 . This fact makes it sensible to talk about (for example) the first, the one-hundredth, or the millionth digit of
. This fact makes it sensible to talk about (for example) the first, the one-hundredth, or the millionth digit of  . Since the natural numbers have cardinality
. Since the natural numbers have cardinality 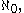 each real number has
each real number has 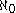 digits in its expansion.
digits in its expansion.Since each real number can be broken into an integer part and a decimal fraction, we get
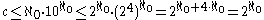
since
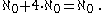
On the other hand, if we map
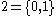 to
to 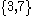 and consider that decimal fractions containing only 3 or 7 are only a part of the real numbers, then we get
and consider that decimal fractions containing only 3 or 7 are only a part of the real numbers, then we get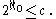
and thus
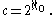
Beth numbers
The sequence of beth numbers is defined by setting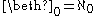 and
and 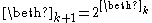 . So
. So  is the second beth number, beth-one:
is the second beth number, beth-one:
The third beth number, beth-two, is the cardinality of the power set of R (i.e. the set of all subsets of the real line
Real line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
):
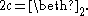
The continuum hypothesis
The famous continuum hypothesis asserts that is also the second aleph number
is also the second aleph numberAleph number
In set theory, a discipline within mathematics, the aleph numbers are a sequence of numbers used to represent the cardinality of infinite sets. They are named after the symbol used to denote them, the Hebrew letter aleph...
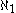 . In other words, the continuum hypothesis states that there is no set
. In other words, the continuum hypothesis states that there is no set 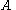 whose cardinality lies strictly between
whose cardinality lies strictly between 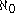 and
and 
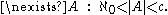
This statement is now known to be independent of the axioms of Zermelo–Fraenkel set theory
Zermelo–Fraenkel set theory
In mathematics, Zermelo–Fraenkel set theory with the axiom of choice, named after mathematicians Ernst Zermelo and Abraham Fraenkel and commonly abbreviated ZFC, is one of several axiomatic systems that were proposed in the early twentieth century to formulate a theory of sets without the paradoxes...
with the axiom of choice (ZFC). That is, both the hypothesis and its negation are consistent with these axioms. In fact, for every nonzero natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
n, the equality
 =
= 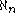 is independent of ZFC. (The case
is independent of ZFC. (The case 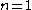 is the continuum hypothesis.) The same is true for most other alephs, although in some cases equality can be ruled out by König's theorem
is the continuum hypothesis.) The same is true for most other alephs, although in some cases equality can be ruled out by König's theoremKönig's theorem (set theory)
In set theory, König's theorem colloquially states that if the axiom of choice holds, I is a set, mi and ni are cardinal numbers for every i in I, and m_i In set theory, König's theorem In set theory, König's theorem (named after the Hungarian mathematician Gyula Kőnig, who published under the...
on the grounds of cofinality
Cofinality
In mathematics, especially in order theory, the cofinality cf of a partially ordered set A is the least of the cardinalities of the cofinal subsets of A....
, e.g.,
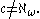 In particular,
In particular,  could be either
could be either 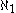 or
or 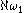 , where
, where 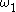 is the first uncountable ordinal
is the first uncountable ordinalFirst uncountable ordinal
In mathematics, the first uncountable ordinal, traditionally denoted by ω1 or sometimes by Ω, is the smallest ordinal number that, considered as a set, is uncountable. It is the supremum of all countable ordinals...
, so it could be either a successor cardinal
Successor cardinal
In the theory of cardinal numbers, we can define a successor operation similar to that in the ordinal numbers. This coincides with the ordinal successor operation for finite cardinals, but in the infinite case they diverge because every infinite ordinal and its successor have the same cardinality...
or a limit cardinal
Limit cardinal
In mathematics, limit cardinals are certain cardinal numbers. A cardinal number λ is a weak limit cardinal if λ is neither a successor cardinal nor zero. This means that one cannot "reach" λ by repeated successor operations...
, and either a regular cardinal
Regular cardinal
In set theory, a regular cardinal is a cardinal number that is equal to its own cofinality. So, crudely speaking, a regular cardinal is one which cannot be broken into a smaller collection of smaller parts....
or a singular cardinal.
Sets with cardinality of the continuum
A great many sets studied in mathematics have cardinality equal to . Some common examples are the following:
. Some common examples are the following:- the real numberReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s
- any (nondegenerate) closed or open intervalInterval (mathematics)In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
in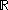 (such as the unit intervalUnit intervalIn mathematics, the unit interval is the closed interval , that is, the set of all real numbers that are greater than or equal to 0 and less than or equal to 1...
(such as the unit intervalUnit intervalIn mathematics, the unit interval is the closed interval , that is, the set of all real numbers that are greater than or equal to 0 and less than or equal to 1...
[0,1]) - the irrational numberIrrational numberIn mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
s - the transcendental numbers
- the Cantor setCantor setIn mathematics, the Cantor set is a set of points lying on a single line segment that has a number of remarkable and deep properties. It was discovered in 1875 by Henry John Stephen Smith and introduced by German mathematician Georg Cantor in 1883....
- Euclidean spaceEuclidean spaceIn mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
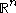
- the complex numberComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s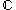
- the power set of the natural numberNatural numberIn mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s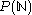 (the set of all subsets of the natural numbers)
(the set of all subsets of the natural numbers) - the set of sequencesSéquencesSéquences is a French-language film magazine originally published in Montreal, Quebec by the Commission des ciné-clubs du Centre catholique du cinéma de Montréal, a Roman Catholic film society. Founded in 1955, the publication was edited for forty years by Léo Bonneville, a member of the Clerics...
of integers (i.e. all functions , often denoted
, often denoted 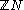 )
) - the set of sequences of real numbers,
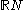
- the set of all continuousContinuous functionIn mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
functions from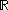 to
to 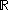
- the Euclidean topologyEuclidean topologyIn mathematics, and especially general topology, the Euclidean topology is an example of a topology given to the set of real numbers, denoted by R...
on (i.e. the set of all open setOpen setThe concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
(i.e. the set of all open setOpen setThe concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
s in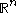 )
) - the Borel σ-algebraBorel algebraIn mathematics, a Borel set is any set in a topological space that can be formed from open sets through the operations of countable union, countable intersection, and relative complement...
on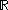 (i.e. the set of all Borel setBorel setIn mathematics, a Borel set is any set in a topological space that can be formed from open sets through the operations of countable union, countable intersection, and relative complement...
(i.e. the set of all Borel setBorel setIn mathematics, a Borel set is any set in a topological space that can be formed from open sets through the operations of countable union, countable intersection, and relative complement...
s in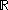 ).
).
Sets with greater cardinality
Sets with cardinality greater than include:
include:- the set of all subsets of
 (i.e., power set
(i.e., power set 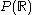 )
) - the set 2R of indicator functions defined on subsets of the reals (the set
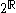 is isomorphic to
is isomorphic to  – the indicator function chooses elements of each subset to include)
– the indicator function chooses elements of each subset to include) - the set
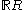 of all functions from
of all functions from 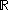 to
to 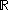
- the Lebesgue σ-algebraLebesgue measureIn measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
of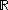 , i.e., the set of all Lebesgue measurable sets in
, i.e., the set of all Lebesgue measurable sets in 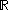 .
. - the Stone–Čech compactificationStone–Cech compactificationIn the mathematical discipline of general topology, Stone–Čech compactification is a technique for constructing a universal map from a topological space X to a compact Hausdorff space βX...
s of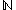 ,
, 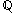 and
and 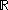 .
.
They all have cardinality
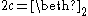 (Beth two).
(Beth two).