
Constant problem
Encyclopedia
In mathematics
, the constant problem is the problem of deciding
if a given expression is equal to zero.
. Often proofs in transcendence theory are proofs by contradiction
, specifically they use some auxiliary function
to create an integer n ≥ 0 which is shown to satisfy n < 1. Clearly this means that n must have the value zero, and so a contradiction arises if one can show that in fact n is not zero.
In many transcendence proofs, proving that n ≠ 0 is very difficult, and hence a lot of work has been done to develop methods that can be used to prove the non-vanishing of certain expressions. The sheer generality of the problem is what makes it difficult to prove general results or come up with general methods for attacking it. The number n that arises may involve integrals, limits
, polynomials, other functions, and determinants of matrices
.
. For example, if x1, ..., xn are real numbers then there is an algorithm for deciding if there are integers a1, ..., an such that
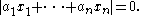
If the expression we are interested in contains a function which oscillates, such as the sine or cosine function, then it has been shown that the problem is undecidable, a result known as Richardson's theorem
. In general, methods specific to the expression being studied are required to prove that it cannot be zero.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the constant problem is the problem of deciding
Decidability (logic)
In logic, the term decidable refers to the decision problem, the question of the existence of an effective method for determining membership in a set of formulas. Logical systems such as propositional logic are decidable if membership in their set of logically valid formulas can be effectively...
if a given expression is equal to zero.
The problem
This problem is also referred to as the identity problem or the method of zero estimates. It has no formal statement as such but refers to a general problem prevalent in transcendence theoryTranscendence theory
Transcendence theory is a branch of number theory that investigates transcendental numbers, in both qualitative and quantitative ways.-Transcendence:...
. Often proofs in transcendence theory are proofs by contradiction
Reductio ad absurdum
In logic, proof by contradiction is a form of proof that establishes the truth or validity of a proposition by showing that the proposition's being false would imply a contradiction...
, specifically they use some auxiliary function
Auxiliary function
In mathematics, auxiliary functions are an important construction in transcendental number theory. They are functions that appear in most proofs in this area of mathematics and that have specific, desirable properties, such as taking the value zero for many arguments, or having a zero of high...
to create an integer n ≥ 0 which is shown to satisfy n < 1. Clearly this means that n must have the value zero, and so a contradiction arises if one can show that in fact n is not zero.
In many transcendence proofs, proving that n ≠ 0 is very difficult, and hence a lot of work has been done to develop methods that can be used to prove the non-vanishing of certain expressions. The sheer generality of the problem is what makes it difficult to prove general results or come up with general methods for attacking it. The number n that arises may involve integrals, limits
Limit (mathematics)
In mathematics, the concept of a "limit" is used to describe the value that a function or sequence "approaches" as the input or index approaches some value. The concept of limit allows mathematicians to define a new point from a Cauchy sequence of previously defined points within a complete metric...
, polynomials, other functions, and determinants of matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
.
Results
In certain cases algorithms or other methods exist for proving that a given expression is non-zero, or of showing that the problem is undecidableUndecidable problem
In computability theory and computational complexity theory, an undecidable problem is a decision problem for which it is impossible to construct a single algorithm that always leads to a correct yes-or-no answer....
. For example, if x1, ..., xn are real numbers then there is an algorithm for deciding if there are integers a1, ..., an such that
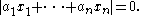
If the expression we are interested in contains a function which oscillates, such as the sine or cosine function, then it has been shown that the problem is undecidable, a result known as Richardson's theorem
Richardson's theorem
In mathematics, Richardson's theorem establishes a limit on the extent to which an algorithm can decide whether certain mathematical expressions are equal...
. In general, methods specific to the expression being studied are required to prove that it cannot be zero.

