Number line
Encyclopedia
In basic mathematics, a number line is a picture of a straight line on which every point is assumed to correspond to a real number
and every real number to a point. Often the integer
s are shown as specially-marked points evenly spaced on the line. Although this image only shows the integers from −9 to 9, the line includes all real number
s, continuing "forever" in each direction, and also numbers not marked that are between the integers. It is often used as an aid in teaching simple addition
and subtraction
, especially involving negative numbers.
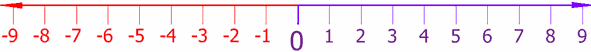It is divided into two symmetric halves by the origin
, i.e. the number zero
.
In advanced mathematics, the expressions real number line, or real line
are typically used to indicate the above-mentioned concept that every point on a straight line corresponds to a single real number, and vice versa.
. Customarily, positive numbers lie on the right side of zero, and negative numbers lie on the left side of zero. An arrowhead on either end of the drawing is meant to suggest that the line continues indefinitely in the positive and negative real number
s, denoted by
. The real numbers consist of irrational number
s and rational numbers, as well as the integer
s, whole number
s, and the natural number
s (the counting numbers).
A line drawn through the origin at right angles to the real number line can be used to represent the imaginary number
s. This line, called imaginary line
, extends the number line to a complex number plane
, with points representing complex number
s.
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
and every real number to a point. Often the integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s are shown as specially-marked points evenly spaced on the line. Although this image only shows the integers from −9 to 9, the line includes all real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s, continuing "forever" in each direction, and also numbers not marked that are between the integers. It is often used as an aid in teaching simple addition
Addition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
and subtraction
Subtraction
In arithmetic, subtraction is one of the four basic binary operations; it is the inverse of addition, meaning that if we start with any number and add any number and then subtract the same number we added, we return to the number we started with...
, especially involving negative numbers.
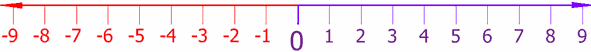
Origin (mathematics)
In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry of the surrounding space. In a Cartesian coordinate system, the origin is the point where the axes of the system intersect...
, i.e. the number zero
0 (number)
0 is both a numberand the numerical digit used to represent that number in numerals.It fulfills a central role in mathematics as the additive identity of the integers, real numbers, and many other algebraic structures. As a digit, 0 is used as a placeholder in place value systems...
.
In advanced mathematics, the expressions real number line, or real line
Real line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
are typically used to indicate the above-mentioned concept that every point on a straight line corresponds to a single real number, and vice versa.
Drawing the number line
The number line is usually represented as being horizontalHorizontal plane
In geometry, physics, astronomy, geography, and related sciences, a plane is said to be horizontal at a given point if it is perpendicular to the gradient of the gravity field at that point— in other words, if apparent gravity makes a plumb bob hang perpendicular to the plane at that point.In...
. Customarily, positive numbers lie on the right side of zero, and negative numbers lie on the left side of zero. An arrowhead on either end of the drawing is meant to suggest that the line continues indefinitely in the positive and negative real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s, denoted by
. The real numbers consist of irrational numberIrrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
s and rational numbers, as well as the integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s, whole number
Whole number
Whole number is a term with inconsistent definitions by different authors. All distinguish whole numbers from fractions and numbers with fractional parts.Whole numbers may refer to:*natural numbers in sense — the positive integers...
s, and the natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s (the counting numbers).
A line drawn through the origin at right angles to the real number line can be used to represent the imaginary number
Imaginary number
An imaginary number is any number whose square is a real number less than zero. When any real number is squared, the result is never negative, but the square of an imaginary number is always negative...
s. This line, called imaginary line
Imaginary line (mathematics)
In geometry, an imaginary line is a straight line that only contains one real point. It can be proven that this point is the intersection point with the conjugated line.It is a special case of an imaginary curve....
, extends the number line to a complex number plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
, with points representing complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s.
See also
- Complex planeComplex planeIn mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
- Extended real number lineExtended real number lineIn mathematics, the affinely extended real number system is obtained from the real number system R by adding two elements: +∞ and −∞ . The projective extended real number system adds a single object, ∞ and makes no distinction between "positive" or "negative" infinity...
- Number formNumber formA number form is a mental map of numbers, which automatically and involuntarily appears whenever someone who experiences number-forms thinks of numbers. Numbers are mapped into distinct spatial locations and the mapping may be different across individuals. Number forms were first documented and...
(neurological phenomenon) - Line (geometry)Line (geometry)The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
- Real lineReal lineIn mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
- Real numberReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
- TimelineChronologyChronology is the science of arranging events in their order of occurrence in time, such as the use of a timeline or sequence of events. It is also "the determination of the actual temporal sequence of past events".Chronology is part of periodization...