Least upper bound axiom
Encyclopedia
The least upper bound axiom, also abbreviated as the LUB axiom, is an axiom
of real analysis
stating that the set R of real number
s has the least-upper-bound property
. That is, if a nonempty set of real numbers has an upper bound
, then it has a least upper bound. It is an axiom in the sense that it cannot be proven by the other real number axioms (namely the order axiom, the field axioms, and the Archimedean axiom). This axiom is very useful since it is essential to the proof that the real number line is a complete metric space
.
The rational number line
Q does not satisfy the LUB axiom and hence is incomplete. An example is the subset of rational numbers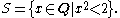
The number 5 is certainly an upper bound for the set. However, this set has no least upper bound in Q: the LUB in this case is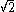
which does not exist in Q, and for any upper bound x ∈ Q, there is another upper bound y ∈ Q with y < x.
The fundamental axiom may be shown to be equivalent to the least upper bound axiom, meaning that assuming either one, it is possible to prove that the other holds as a theorem
.
The least upper bound axiom is also equivalent to the Bolzano–Weierstrass theorem
:
The axiom is also equivalent to the completeness of the real numbers (in the sense that the real numbers are the only complete Archimedean ordered field). The least upper bound property implies that the limit superior and limit inferior
of a bounded sequence are well-defined. When applied to a Cauchy sequence
, they coincide and must agree with the limit of the sequence. Conversely, if an Archimedean ordered field were complete, then from any nonempty bounded set S above one can extract an increasing sequence such that no element of S is greater than every element of the sequence. Completeness then implies convergence of the sequence to the least upper bound of S.
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
of real analysis
Real analysis
Real analysis, is a branch of mathematical analysis dealing with the set of real numbers and functions of a real variable. In particular, it deals with the analytic properties of real functions and sequences, including convergence and limits of sequences of real numbers, the calculus of the real...
stating that the set R of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s has the least-upper-bound property
Least-upper-bound property
In mathematics, the least-upper-bound property is a fundamental property of the real numbers and certain other ordered sets. The property states that any non-empty set of real numbers that has an upper bound necessarily has a least upper bound ....
. That is, if a nonempty set of real numbers has an upper bound
Upper bound
In mathematics, especially in order theory, an upper bound of a subset S of some partially ordered set is an element of P which is greater than or equal to every element of S. The term lower bound is defined dually as an element of P which is lesser than or equal to every element of S...
, then it has a least upper bound. It is an axiom in the sense that it cannot be proven by the other real number axioms (namely the order axiom, the field axioms, and the Archimedean axiom). This axiom is very useful since it is essential to the proof that the real number line is a complete metric space
Complete space
In mathematical analysis, a metric space M is called complete if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in M converges in M....
.
The rational number line
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
Q does not satisfy the LUB axiom and hence is incomplete. An example is the subset of rational numbers
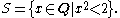
The number 5 is certainly an upper bound for the set. However, this set has no least upper bound in Q: the LUB in this case is
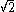which does not exist in Q, and for any upper bound x ∈ Q, there is another upper bound y ∈ Q with y < x.Equivalent axioms
There are a variety of axioms that are equivalent to the least upper bound axiom. Among these is the following axiom, known as the fundamental axiom of analysis by :- Every non-decreasing sequence of real numberReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s which is bounded above tends to a limitLimit of a sequenceThe limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
.
The fundamental axiom may be shown to be equivalent to the least upper bound axiom, meaning that assuming either one, it is possible to prove that the other holds as a theorem
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
.
The least upper bound axiom is also equivalent to the Bolzano–Weierstrass theorem
Bolzano–Weierstrass theorem
In real analysis, the Bolzano–Weierstrass theorem is a fundamental result about convergence in a finite-dimensional Euclidean space Rn. The theorem states thateach bounded sequence in Rn has a convergent subsequence...
:
- Every bounded sequence of real numbers has a convergent subsequence.
The axiom is also equivalent to the completeness of the real numbers (in the sense that the real numbers are the only complete Archimedean ordered field). The least upper bound property implies that the limit superior and limit inferior
Limit superior and limit inferior
In mathematics, the limit inferior and limit superior of a sequence can be thought of as limiting bounds on the sequence...
of a bounded sequence are well-defined. When applied to a Cauchy sequence
Cauchy sequence
In mathematics, a Cauchy sequence , named after Augustin-Louis Cauchy, is a sequence whose elements become arbitrarily close to each other as the sequence progresses...
, they coincide and must agree with the limit of the sequence. Conversely, if an Archimedean ordered field were complete, then from any nonempty bounded set S above one can extract an increasing sequence such that no element of S is greater than every element of the sequence. Completeness then implies convergence of the sequence to the least upper bound of S.
See also
- SupremumSupremumIn mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
- Dedekind cutDedekind cutIn mathematics, a Dedekind cut, named after Richard Dedekind, is a partition of the rationals into two non-empty parts A and B, such that all elements of A are less than all elements of B, and A contains no greatest element....
- Completeness (order theory)Completeness (order theory)In the mathematical area of order theory, completeness properties assert the existence of certain infima or suprema of a given partially ordered set . A special use of the term refers to complete partial orders or complete lattices...
- Fundamental axiom of analysis