
Real closed field
Encyclopedia
In mathematics
, a real closed field is a field
F that has the same first-order properties as the field of real numbers. Some examples are the field of real numbers, the field of real algebraic numbers, and the field of hyperreal number
s.
If F is an ordered field (not just orderable, but a definite ordering is fixed as part of the structure), the Artin–Schreier theorem states that F has an algebraic extension, called the real closure K of F, such that K is a real closed field whose ordering is an extension of the given ordering on F, and is unique up to a unique isomorphism of fields (note that every ring homomorphism
between real closed fields automatically is order preserving
, because x ≤ y if and only if ∃z y = x+z2). For example, the real closure of the rational numbers is the field of real algebraic number
of real algebraic number
s. The theorem is named for Emil Artin
and Otto Schreier
, who proved it in 1926.
If F is a field (so this time, no order is fixed, and it is even not necessary to assume that F is orderable) then F still has a real closure, which in general is not a field anymore, but a
real closed ring
. For example the real closure of the field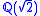 is the ring
is the ring  (the two copies correspond to the two orderings of
(the two copies correspond to the two orderings of 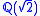 ). Whereas the real closure of the ordered subfield
). Whereas the real closure of the ordered subfield 
of is again the field
is again the field  .
.
axioms
one obtains a first-order theory. Tarski (1951) proved that the theory of real closed fields in the first order language of partially-ordered rings
(consisting of the binary predicate symbols "=" and "≤", the operations of addition, subtraction and multiplication and the constant symbols 0,1) admits elimination of quantifiers. The most important model theoretic
consequences hereof: The theory of real closed fields is complete
, o-minimal and decidable
.
Decidability means that there exists at least one decision procedure, i.e., a well-defined algorithm for determining whether a sentence in the first order language of real closed fields is true. Euclidean geometry
(without the ability to measure angles) is also a model
of the real field axioms, and thus is also decidable.
The decision procedures are not necessarily practical. The algorithmic complexities of all known decision procedures for real closed fields are very high, so that practical execution times can be prohibitively high except for very simple problems.
The algorithm Tarski proposed for quantifier elimination
has NONELEMENTARY
complexity, meaning that no tower can bound the execution time of the algorithm if n is the size of the problem. Davenport and Heintz (1988) proved that quantifier elimination is in fact (at least) doubly exponential: there exists a family Φn of formulas with n quantifiers, of length O(n) and constant degree such that any quantifier-free formula equivalent to Φn must involve polynomials of degree
can bound the execution time of the algorithm if n is the size of the problem. Davenport and Heintz (1988) proved that quantifier elimination is in fact (at least) doubly exponential: there exists a family Φn of formulas with n quantifiers, of length O(n) and constant degree such that any quantifier-free formula equivalent to Φn must involve polynomials of degree  and length
and length 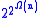 , using the Ω asymptotic notation.
, using the Ω asymptotic notation.
Basu and Roy (1996) proved that there exists a well-behaved algorithm to decide the truth of a formula ∃x1,…,∃xk P1(x1,…,xk)⋈0∧…∧Ps(x1,…,xk)⋈0 where ⋈ is <, > or =, with complexity in arithmetic operations sk+1dO(k).
. An equivalent statement is that for any real number, there are integers both larger and smaller. A non-archimedean field is, of course, a field that is not archimedean, and there are real closed non-archimedean fields; for example any field of hyperreal numbers is real closed and non-archimedean.
The archimedean property is related to the concept of cofinality
. A set X contained in an ordered set F is cofinal in F if for every y in F there is an x in X such that y < x. In other words, X is an unbounded sequence in F. The cofinality of F is the size of the smallest cofinal set, which is to say, the size of the smallest cardinality giving an unbounded sequence. For example natural numbers are cofinal in the reals, and the cofinality of the reals is therefore .
.
We have therefore the following invariants defining the nature of a real closed field F:
To this we may add
These three cardinal numbers tell us much about the order properties of any real closed field, though it may be difficult to discover what they are, especially if we are not willing to invoke generalized continuum hypothesis
. There are also particular properties which may or may not hold:
. If the continuum hypothesis holds, all real closed fields with cardinality the continuum and having the η1 property are order isomorphic. This unique field Ϝ can be defined by means of an ultrapower
, as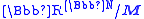 , where M is a maximal ideal not leading to a field order-isomorphic to
, where M is a maximal ideal not leading to a field order-isomorphic to 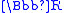 . This is the most commonly used hyperreal number field in nonstandard analysis, and its uniqueness is equivalent to the continuum hypothesis. (Even without the continuum hypothesis we have that if the cardinality of the continuum is
. This is the most commonly used hyperreal number field in nonstandard analysis, and its uniqueness is equivalent to the continuum hypothesis. (Even without the continuum hypothesis we have that if the cardinality of the continuum is
 then we have a unique ηβ field of size ηβ.)
then we have a unique ηβ field of size ηβ.)
Moreover, we do not need ultrapowers to construct Ϝ, we can do so much more constructively as the subfield of series with a countable number of nonzero terms of the field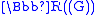 of formal power series
of formal power series
on the Sierpiński group.
Ϝ however is not a complete field; if we take its completion, we end up with a field Κ of larger cardinality. Ϝ has the cardinality of the continuum which by hypothesis is , Κ has cardinality
, Κ has cardinality  , and contains Ϝ as a dense subfield. It is not an ultrapower but it is a hyperreal field, and hence a suitable field for the usages of nonstandard analysis. It can be seen to be the higher-dimensional analogue of the real numbers; with cardinality
, and contains Ϝ as a dense subfield. It is not an ultrapower but it is a hyperreal field, and hence a suitable field for the usages of nonstandard analysis. It can be seen to be the higher-dimensional analogue of the real numbers; with cardinality  instead of
instead of  , cofinality
, cofinality  instead of
instead of 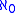 , and weight
, and weight 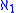 instead of
instead of  , and with the η1 property in place of the η0 property (which merely means between any two real numbers we can find another).
, and with the η1 property in place of the η0 property (which merely means between any two real numbers we can find another).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a real closed field is a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
F that has the same first-order properties as the field of real numbers. Some examples are the field of real numbers, the field of real algebraic numbers, and the field of hyperreal number
Hyperreal number
The system of hyperreal numbers represents a rigorous method of treating the infinite and infinitesimal quantities. The hyperreals, or nonstandard reals, *R, are an extension of the real numbers R that contains numbers greater than anything of the form1 + 1 + \cdots + 1. \, Such a number is...
s.
Definitions
A real closed field is a field F in which any of the following equivalent conditions are true:- F is elementarily equivalent to the real numbers. In other words it has the same first-order properties as the reals: any sentence in the first-order language of fields is true in F if and only if it is true in the reals.
- There is a total orderTotal orderIn set theory, a total order, linear order, simple order, or ordering is a binary relation on some set X. The relation is transitive, antisymmetric, and total...
on F making it an ordered fieldOrdered fieldIn mathematics, an ordered field is a field together with a total ordering of its elements that is compatible with the field operations. Historically, the axiomatization of an ordered field was abstracted gradually from the real numbers, by mathematicians including David Hilbert, Otto Hölder and...
such that, in this ordering, every positive element of F is a square in F and any polynomialPolynomialIn mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
of odd degreeDegree (mathematics)In mathematics, there are several meanings of degree depending on the subject.- Unit of angle :A degree , usually denoted by ° , is a measurement of a plane angle, representing 1⁄360 of a turn...
with coefficients in F has at least one root in F. - F is a formally real fieldFormally real fieldIn mathematics, in particular in field theory and real algebra, a formally real field is a field that admits an ordering which makes it an ordered field.-Alternative Definitions:...
such that every polynomial of odd degree with coefficients in F has at least one root in F, and for every element a of F there is b in F such that a = b2 or a = −b2. - F is not algebraically closed but its algebraic closure is a finite extension.
- F is not algebraically closed but the field extensionField extensionIn abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
 is algebraically closed.
is algebraically closed. - There is an ordering on F which does not extend to an ordering on any proper algebraic extensionAlgebraic extensionIn abstract algebra, a field extension L/K is called algebraic if every element of L is algebraic over K, i.e. if every element of L is a root of some non-zero polynomial with coefficients in K. Field extensions that are not algebraic, i.e...
of F. - F is a formally real field such that no proper algebraic extension of F is formally real. (In other words, the field is maximal in an algebraic closure with respect to the property of being formally real.)
- There is an ordering on F making it an ordered field such that, in this ordering, the intermediate value theoremIntermediate value theoremIn mathematical analysis, the intermediate value theorem states that for each value between the least upper bound and greatest lower bound of the image of a continuous function there is at least one point in its domain that the function maps to that value....
holds for all polynomials over F. - F is a field and a real closed ringReal closed ringIn mathematics, a real closed ring is a commutative ring A thatis a subring of a product of real closed fields, which is closed undercontinuous semi-algebraic functions defined over the integers.- Examples of real closed rings :...
.
If F is an ordered field (not just orderable, but a definite ordering is fixed as part of the structure), the Artin–Schreier theorem states that F has an algebraic extension, called the real closure K of F, such that K is a real closed field whose ordering is an extension of the given ordering on F, and is unique up to a unique isomorphism of fields (note that every ring homomorphism
Ring homomorphism
In ring theory or abstract algebra, a ring homomorphism is a function between two rings which respects the operations of addition and multiplication....
between real closed fields automatically is order preserving
Order isomorphism
In the mathematical field of order theory an order isomorphism is a special kind of monotone function that constitutes a suitable notion of isomorphism for partially ordered sets . Whenever two posets are order isomorphic, they can be considered to be "essentially the same" in the sense that one of...
, because x ≤ y if and only if ∃z y = x+z2). For example, the real closure of the rational numbers is the field
 of real algebraic number
of real algebraic numberAlgebraic number
In mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
s. The theorem is named for Emil Artin
Emil Artin
Emil Artin was an Austrian-American mathematician of Armenian descent.-Parents:Emil Artin was born in Vienna to parents Emma Maria, née Laura , a soubrette on the operetta stages of Austria and Germany, and Emil Hadochadus Maria Artin, Austrian-born of Armenian descent...
and Otto Schreier
Otto Schreier
Otto Schreier was an Austrian mathematician who made major contributions in combinatorial group theory and in the topology of Lie groups. He studied mathematics at the University of Vienna and obtained his doctorate in 1923, under the supervision of Philipp Furtwängler...
, who proved it in 1926.
If F is a field (so this time, no order is fixed, and it is even not necessary to assume that F is orderable) then F still has a real closure, which in general is not a field anymore, but a
real closed ring
Real closed ring
In mathematics, a real closed ring is a commutative ring A thatis a subring of a product of real closed fields, which is closed undercontinuous semi-algebraic functions defined over the integers.- Examples of real closed rings :...
. For example the real closure of the field
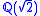 is the ring
is the ring  (the two copies correspond to the two orderings of
(the two copies correspond to the two orderings of 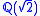 ). Whereas the real closure of the ordered subfield
). Whereas the real closure of the ordered subfield 
of
 is again the field
is again the field  .
.Model Theory: decidability and quantifier elimination
The theory of real closed fields was invented by algebraists, but taken up with enthusiasm by logicians. By adding to the ordered fieldOrdered field
In mathematics, an ordered field is a field together with a total ordering of its elements that is compatible with the field operations. Historically, the axiomatization of an ordered field was abstracted gradually from the real numbers, by mathematicians including David Hilbert, Otto Hölder and...
axioms
- an axiom asserting that every positive number has a square root, and
- an axiom scheme asserting that all polynomialPolynomialIn mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s of odd degree have at least one root,
one obtains a first-order theory. Tarski (1951) proved that the theory of real closed fields in the first order language of partially-ordered rings
Partially-ordered ring
In abstract algebra, a partially-ordered ring is a ring , together with a compatible partial order, i.e. a partial order \leq on the underlying set A that is compatible with the ring operations in the sense that it satisfies:x\leq y implies x + z\leq y + zand0\leq x and 0\leq y imply that 0\leq...
(consisting of the binary predicate symbols "=" and "≤", the operations of addition, subtraction and multiplication and the constant symbols 0,1) admits elimination of quantifiers. The most important model theoretic
Model theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
consequences hereof: The theory of real closed fields is complete
Complete theory
In mathematical logic, a theory is complete if it is a maximal consistent set of sentences, i.e., if it is consistent, and none of its proper extensions is consistent...
, o-minimal and decidable
Decidability (logic)
In logic, the term decidable refers to the decision problem, the question of the existence of an effective method for determining membership in a set of formulas. Logical systems such as propositional logic are decidable if membership in their set of logically valid formulas can be effectively...
.
Decidability means that there exists at least one decision procedure, i.e., a well-defined algorithm for determining whether a sentence in the first order language of real closed fields is true. Euclidean geometry
Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
(without the ability to measure angles) is also a model
Model theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
of the real field axioms, and thus is also decidable.
The decision procedures are not necessarily practical. The algorithmic complexities of all known decision procedures for real closed fields are very high, so that practical execution times can be prohibitively high except for very simple problems.
The algorithm Tarski proposed for quantifier elimination
Quantifier elimination
Quantifier elimination is a concept of simplification used in mathematical logic, model theory, and theoretical computer science. One way of classifying formulas is by the amount of quantification...
has NONELEMENTARY
NONELEMENTARY
In computational complexity theory, the complexity class NONELEMENTARY is the complement of the class ELEMENTARY.Example decidable problems in NONELEMENTARY this class are:* the problem of regular expression equivalence with not...
complexity, meaning that no tower
 can bound the execution time of the algorithm if n is the size of the problem. Davenport and Heintz (1988) proved that quantifier elimination is in fact (at least) doubly exponential: there exists a family Φn of formulas with n quantifiers, of length O(n) and constant degree such that any quantifier-free formula equivalent to Φn must involve polynomials of degree
can bound the execution time of the algorithm if n is the size of the problem. Davenport and Heintz (1988) proved that quantifier elimination is in fact (at least) doubly exponential: there exists a family Φn of formulas with n quantifiers, of length O(n) and constant degree such that any quantifier-free formula equivalent to Φn must involve polynomials of degree  and length
and length 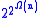 , using the Ω asymptotic notation.
, using the Ω asymptotic notation.Basu and Roy (1996) proved that there exists a well-behaved algorithm to decide the truth of a formula ∃x1,…,∃xk P1(x1,…,xk)⋈0∧…∧Ps(x1,…,xk)⋈0 where ⋈ is <, > or =, with complexity in arithmetic operations sk+1dO(k).
Order properties
A crucially important property of the real numbers is that it is an archimedean field, meaning it has the archimedean property that for any real number, there is an integer larger than it in absolute valueAbsolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
. An equivalent statement is that for any real number, there are integers both larger and smaller. A non-archimedean field is, of course, a field that is not archimedean, and there are real closed non-archimedean fields; for example any field of hyperreal numbers is real closed and non-archimedean.
The archimedean property is related to the concept of cofinality
Cofinality
In mathematics, especially in order theory, the cofinality cf of a partially ordered set A is the least of the cardinalities of the cofinal subsets of A....
. A set X contained in an ordered set F is cofinal in F if for every y in F there is an x in X such that y < x. In other words, X is an unbounded sequence in F. The cofinality of F is the size of the smallest cofinal set, which is to say, the size of the smallest cardinality giving an unbounded sequence. For example natural numbers are cofinal in the reals, and the cofinality of the reals is therefore
 .
.We have therefore the following invariants defining the nature of a real closed field F:
- The cardinality of F.
- The cofinality of F.
To this we may add
- The weight of F, which is the minimum size of a dense subset of F.
These three cardinal numbers tell us much about the order properties of any real closed field, though it may be difficult to discover what they are, especially if we are not willing to invoke generalized continuum hypothesis
Continuum hypothesis
In mathematics, the continuum hypothesis is a hypothesis, advanced by Georg Cantor in 1874, about the possible sizes of infinite sets. It states:Establishing the truth or falsehood of the continuum hypothesis is the first of Hilbert's 23 problems presented in the year 1900...
. There are also particular properties which may or may not hold:
- A field F is complete if there is no ordered field K properly containing F such that F is dense in K. If the cofinality of K is κ, this is equivalent to saying Cauchy sequences indexed by κ are convergent in F.
- An ordered field F has the ηα property for the ordinal number α if for any two subsets L and U of F of cardinality less than
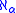 , at least one of which is nonempty, and such that every element of L is less than every element of U, there is an element x in F with x larger than every element of L and smaller than every element of U. This is closely related to the model-theoretic property of being a saturated modelSaturated modelIn mathematical logic, and particularly in its subfield model theory, a saturated model M is one which realizes as many complete types as may be "reasonably expected" given its size...
, at least one of which is nonempty, and such that every element of L is less than every element of U, there is an element x in F with x larger than every element of L and smaller than every element of U. This is closely related to the model-theoretic property of being a saturated modelSaturated modelIn mathematical logic, and particularly in its subfield model theory, a saturated model M is one which realizes as many complete types as may be "reasonably expected" given its size...
; any two real closed fields are ηα if and only if they are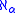 -saturated, and moreover two ηα real closed fields both of cardinality
-saturated, and moreover two ηα real closed fields both of cardinality  are order isomorphic.
are order isomorphic.
The generalized continuum hypothesis
The characteristics of real closed fields become much simpler if we are willing to assume the generalized continuum hypothesisContinuum hypothesis
In mathematics, the continuum hypothesis is a hypothesis, advanced by Georg Cantor in 1874, about the possible sizes of infinite sets. It states:Establishing the truth or falsehood of the continuum hypothesis is the first of Hilbert's 23 problems presented in the year 1900...
. If the continuum hypothesis holds, all real closed fields with cardinality the continuum and having the η1 property are order isomorphic. This unique field Ϝ can be defined by means of an ultrapower
Ultraproduct
The ultraproduct is a mathematical construction that appears mainly in abstract algebra and in model theory, a branch of mathematical logic. An ultraproduct is a quotient of the direct product of a family of structures. All factors need to have the same signature...
, as
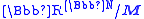 , where M is a maximal ideal not leading to a field order-isomorphic to
, where M is a maximal ideal not leading to a field order-isomorphic to 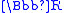 . This is the most commonly used hyperreal number field in nonstandard analysis, and its uniqueness is equivalent to the continuum hypothesis. (Even without the continuum hypothesis we have that if the cardinality of the continuum is
. This is the most commonly used hyperreal number field in nonstandard analysis, and its uniqueness is equivalent to the continuum hypothesis. (Even without the continuum hypothesis we have that if the cardinality of the continuum is then we have a unique ηβ field of size ηβ.)
then we have a unique ηβ field of size ηβ.)Moreover, we do not need ultrapowers to construct Ϝ, we can do so much more constructively as the subfield of series with a countable number of nonzero terms of the field
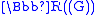 of formal power series
of formal power seriesFormal power series
In mathematics, formal power series are a generalization of polynomials as formal objects, where the number of terms is allowed to be infinite; this implies giving up the possibility to substitute arbitrary values for indeterminates...
on the Sierpiński group.
Ϝ however is not a complete field; if we take its completion, we end up with a field Κ of larger cardinality. Ϝ has the cardinality of the continuum which by hypothesis is
 , Κ has cardinality
, Κ has cardinality  , and contains Ϝ as a dense subfield. It is not an ultrapower but it is a hyperreal field, and hence a suitable field for the usages of nonstandard analysis. It can be seen to be the higher-dimensional analogue of the real numbers; with cardinality
, and contains Ϝ as a dense subfield. It is not an ultrapower but it is a hyperreal field, and hence a suitable field for the usages of nonstandard analysis. It can be seen to be the higher-dimensional analogue of the real numbers; with cardinality  instead of
instead of  , cofinality
, cofinality  instead of
instead of 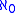 , and weight
, and weight 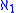 instead of
instead of  , and with the η1 property in place of the η0 property (which merely means between any two real numbers we can find another).
, and with the η1 property in place of the η0 property (which merely means between any two real numbers we can find another).Examples of real closed fields
- the real algebraic numbers
- the computable numberComputable numberIn mathematics, particularly theoretical computer science and mathematical logic, the computable numbers, also known as the recursive numbers or the computable reals, are the real numbers that can be computed to within any desired precision by a finite, terminating algorithm...
s - the definable numberDefinable numberA real number a is first-order definable in the language of set theory, without parameters, if there is a formula φ in the language of set theory, with one free variable, such that a is the unique real number such that φ holds in the standard model of set theory .For the purposes of this article,...
s - the real numberReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s - superreal numberSuperreal numberIn abstract algebra, the superreal numbers are a class of extensions of the real numbers, introduced by H. Garth Dales and W. Hugh Woodin as a generalization of the hyperreal numbers and primarily of interest in non-standard analysis, model theory, and the study of Banach algebras...
s - hyperreal numberHyperreal numberThe system of hyperreal numbers represents a rigorous method of treating the infinite and infinitesimal quantities. The hyperreals, or nonstandard reals, *R, are an extension of the real numbers R that contains numbers greater than anything of the form1 + 1 + \cdots + 1. \, Such a number is...
s - the Puiseux seriesPuiseux seriesIn mathematics, Puiseux series are a generalization of formal power series, first introduced by Isaac Newton in 1676 and rediscovered by Victor Puiseux in 1850, that allows for negative and fractional exponents of the indeterminate...
with real coefficients

