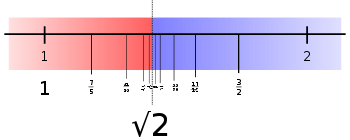
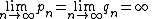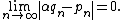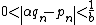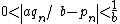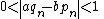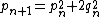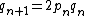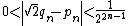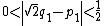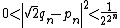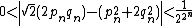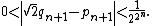Square root of 2
Encyclopedia

Algebraic number
In mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
that, when multiplied by itself, gives the number 2. It is more precisely called the principal square root of 2, to distinguish it from the negative number with the same property.
Geometrically the square root
Square root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
of 2 is the length of a diagonal across a square with sides of one unit of length; this follows from the Pythagorean theorem
Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
. It was probably the first number known to be irrational
Irrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
.
Its numerical value truncated to 65 decimal places
Decimal
The decimal numeral system has ten as its base. It is the numerical base most widely used by modern civilizations....
is:
| Binary Binary numeral system The binary numeral system, or base-2 number system, represents numeric values using two symbols, 0 and 1. More specifically, the usual base-2 system is a positional notation with a radix of 2... |
1.0110101000001001111... |
| Decimal Decimal The decimal numeral system has ten as its base. It is the numerical base most widely used by modern civilizations.... |
1.4142135623730950488... |
| Hexadecimal Hexadecimal In mathematics and computer science, hexadecimal is a positional numeral system with a radix, or base, of 16. It uses sixteen distinct symbols, most often the symbols 0–9 to represent values zero to nine, and A, B, C, D, E, F to represent values ten to fifteen... |
1.6A09E667F3BCC908B2F... |
| Continued fraction Continued fraction In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on... |
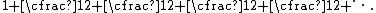 |
History

Yale Babylonian Collection
Comprising some 45,000 items, the Yale Babylonian Collection is an independent branch of the Yale University Library housed on the Yale University campus in Sterling Memorial Library at New Haven, Connecticut, United States....
(c. 1800–1600 BCE) gives an approximation of
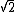 in four sexagesimal figures, which is about six decimal
in four sexagesimal figures, which is about six decimalDecimal
The decimal numeral system has ten as its base. It is the numerical base most widely used by modern civilizations....
figures:
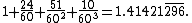
Another early close approximation of this number is given in ancient Indian
History of India
The history of India begins with evidence of human activity of Homo sapiens as long as 75,000 years ago, or with earlier hominids including Homo erectus from about 500,000 years ago. The Indus Valley Civilization, which spread and flourished in the northwestern part of the Indian subcontinent from...
mathematical texts, the Sulbasutras
Sulba Sutras
The Shulba Sutras or Śulbasūtras are sutra texts belonging to the Śrauta ritual and containing geometry related to fire-altar construction.- Purpose and origins :...
(c. 800–200 BCE) as follows: Increase the length [of the side] by its third and this third by its own fourth less the thirty-fourth part of that fourth. That is,
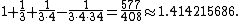
This ancient Indian approximation is the seventh in a sequence of increasingly accurate approximations based on the sequence of Pell number
Pell number
In mathematics, the Pell numbers are an infinite sequence of integers that have been known since ancient times, the denominators of the closest rational approximations to the square root of 2. This sequence of approximations begins 1/1, 3/2, 7/5, 17/12, and 41/29, so the sequence of Pell numbers...
s, that can be derived from the continued fraction
Continued fraction
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on...
expansion of
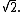
Pythagoreans
Pythagoreanism
Pythagoreanism was the system of esoteric and metaphysical beliefs held by Pythagoras and his followers, the Pythagoreans, who were considerably influenced by mathematics. Pythagoreanism originated in the 5th century BCE and greatly influenced Platonism...
discovered that the diagonal of a square is incommensurable with its side, or in modern language, that the square root of two is irrational
Irrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
. Little is known with certainty about the time or circumstances of this discovery, but the name of Hippasus
Hippasus
Hippasus of Metapontum in Magna Graecia, was a Pythagorean philosopher. Little is known about his life or his beliefs, but he is sometimes credited with the discovery of the existence of irrational numbers.-Life:...
of Metapontum is often mentioned. For a while, ancient Greeks treated as an official secret the discovery that the square root of two is irrational, and, according to legend, Hippasus was murdered for divulging it. The square root of two is occasionally called "Pythagoras's number" or "Pythagoras's Constant", for example .
Computation algorithms
There are a number of algorithms for approximating the square root of 2, which in expressions as a ratio of integers or as a decimal can only be approximated. The most common algorithm for this, one used as a basis in many computers and calculators, is the Babylonian method of computing square roots, which is one of many methods of computing square rootsMethods of computing square roots
There are several methods for calculating the principal square root of a nonnegative real number. For the square roots of a negative or complex number, see below.- Rough estimation :...
. It goes as follows:
First, pick a guess, a0 > 0; the value of the guess affects only how many iterations are required to reach an approximation of a certain accuracy. Then, using that guess, iterate through the following recursive
Recursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
computation:
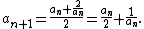
The more iterations through the algorithm (that is, the more computations performed and the greater "n"), the better approximation of the square root of 2 is achieved. Each iteration approximately doubles the number of correct digits. Starting with a0 = 1 the next approximations are
- 3/2 = 1.5
- 17/12 = 1.416...
- 577/408 = 1.414215...
- 665857/470832 = 1.4142135623746...
The value of √2 was calculated to 137,438,953,444 decimal places by Yasumasa Kanada
Yasumasa Kanada
is a Japanese mathematician most known for his numerous world records over the past three decades for calculating digits of π. He has set the record 11 of the past 21 times....
's team in 1997.
In February 2006 the record for the calculation of √2 was eclipsed with the use of a home computer. Shigeru Kondo calculated 200,000,000,000 decimal places in slightly over 13 days and 14 hours using a 3.6 GHz PC with 16 GiB
Gibibyte
The gibibyte is a standards-based binary multiple of the byte, a unit of digital information storage. The gibibyte unit symbol is GiB....
of memory.
Among mathematical constants with computationally challenging decimal expansions, only
Pi
' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
has been calculated more precisely.
Proofs of irrationality
A short proof of this result is to obtain it from rational root theorem, that if p(x) is a monic polynomial with integer coefficients, then any rational root of p(x) is necessarily an integer. Applying this to the polynomial p(x) = x2 − 2, it follows that √2 is either an integer or irrational. Because √2 is not an integer (2 is not a perfect square), √2 must therefore be irrational.See quadratic irrational
Quadratic irrational
In mathematics, a quadratic irrational is an irrational number that is the solution to some quadratic equation with rational coefficients...
or infinite descent#Irrationality of √k if it is not an integer for a proof that the square root of any non-square natural number is irrational.
Proof by infinite descent
One proof of the number's irrationality is the following proof by infinite descentInfinite descent
In mathematics, a proof by infinite descent is a particular kind of proof by contradiction which relies on the fact that the natural numbers are well ordered. One typical application is to show that a given equation has no solutions. Assuming a solution exists, one shows that another exists, that...
. It is also a proof by contradiction
Reductio ad absurdum
In logic, proof by contradiction is a form of proof that establishes the truth or validity of a proposition by showing that the proposition's being false would imply a contradiction...
, which means the proposition is proved by assuming that the opposite of the proposition is true and showing that this assumption is false, thereby implying that the proposition must be true.
- Assume that √2 is a rational number, meaning that there exists an integer a and an integer b in general such that a / b = √2.
- Then √2 can be written as an irreducible fractionIrreducible fractionAn irreducible fraction is a vulgar fraction in which the numerator and denominator are smaller than those in any other equivalent vulgar fraction...
a / b such that a and b are coprimeCoprimeIn number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
integers and (a / b)2 = 2. - It follows that a2 / b2 = 2 and a2 = 2 b2. ( (a / b)n = an / bn )
- Therefore a2 is even because it is equal to 2 b2. (2 b2 is necessarily even because it is 2 times another whole number and even numbers are multiples of 2.)
- It follows that a must be even (as squares of odd integers are never even).
- Because a is even, there exists an integer k that fulfills: a = 2k.
- Substituting 2k from step 6 for a in the second equation of step 3: 2b2 = (2k)2 is equivalent to 2b2 = 4k2, which is equivalent to b2 = 2k2.
- Because 2k2 is divisible by two and therefore even, and because 2k2 = b2, it follows that b2 is also even which means that b is even.
- By steps 5 and 8 a and b are both even, which contradicts that a / b is irreducible as stated in step 2.
-
- Q.E.D.Q.E.D.Q.E.D. is an initialism of the Latin phrase , which translates as "which was to be demonstrated". The phrase is traditionally placed in its abbreviated form at the end of a mathematical proof or philosophical argument when what was specified in the enunciation — and in the setting-out —...
- Q.E.D.
Because there is a contradiction, the assumption (1) that √2 is a rational number must be false. By the law of excluded middle
Law of excluded middle
In logic, the law of excluded middle is the third of the so-called three classic laws of thought. It states that for any proposition, either that proposition is true, or its negation is....
, the opposite is proven: √2 is irrational.
This proof was hinted by Aristotle
Aristotle
Aristotle was a Greek philosopher and polymath, a student of Plato and teacher of Alexander the Great. His writings cover many subjects, including physics, metaphysics, poetry, theater, music, logic, rhetoric, linguistics, politics, government, ethics, biology, and zoology...
, in his Analytica Priora
Prior Analytics
The Prior Analytics is Aristotle's work on deductive reasoning, specifically the syllogism. It is also part of his Organon, which is the instrument or manual of logical and scientific methods....
, §I.23. It appeared first as a full proof in Euclid's
Euclid
Euclid , fl. 300 BC, also known as Euclid of Alexandria, was a Greek mathematician, often referred to as the "Father of Geometry". He was active in Alexandria during the reign of Ptolemy I...
Elements
Euclid's Elements
Euclid's Elements is a mathematical and geometric treatise consisting of 13 books written by the Greek mathematician Euclid in Alexandria c. 300 BC. It is a collection of definitions, postulates , propositions , and mathematical proofs of the propositions...
, as proposition 117 of Book X. However, since the early 19th century historians agree that this proof is an interpolation
Interpolation (manuscripts)
An interpolation, in relation to literature and especially ancient manuscripts, is an entry or passage in a text that was not written by the original author...
and not attributable to Euclid.
Proof by unique factorization
An alternative proof uses the same approach with the fundamental theorem of arithmeticFundamental theorem of arithmetic
In number theory, the fundamental theorem of arithmetic states that any integer greater than 1 can be written as a unique product of prime numbers...
which says every integer greater than 1 has a unique factorization into powers of primes.
- Assume that √2 is a rational number. Then there are integers a and b such that a is coprimeCoprimeIn number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
to b and √2 = a / b. In other words, √2 can be written as an irreducible fractionIrreducible fractionAn irreducible fraction is a vulgar fraction in which the numerator and denominator are smaller than those in any other equivalent vulgar fraction...
. - The value of b cannot be 1 as there is no integer a the square of which is 2.
- There must be a prime p which divides b and which does not divide a otherwise the fraction would not be irreducible.
- The square of a can be factored as the product of the primes into which a is factored but with each power doubled.
- Therefore by unique factorization the prime p which divides b, and also its square, cannot divide the square of a.
- Therefore the square of an irreducible fraction cannot be reduced to an integer.
- Therefore the square root of 2 cannot be a rational number.
This proof can be generalized to show that any root of any natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
which is not the square of a natural number is irrational. The article quadratic irrational
Quadratic irrational
In mathematics, a quadratic irrational is an irrational number that is the solution to some quadratic equation with rational coefficients...
gives a proof of the same result but not using the fundamental theorem of arithmetic.
Proof by infinite descent, not involving factoring
The following reductio ad absurdumReductio ad absurdum
In logic, proof by contradiction is a form of proof that establishes the truth or validity of a proposition by showing that the proposition's being false would imply a contradiction...
argument showing the irrationality of √2 is less well-known. It uses the additional information 2 > √2 > 1 so that 1 > √2 − 1 > 0.
- Assume that √2 is a rational number. This would mean that there exist positive integers m and n with n ≠ 0 such that m/n = √2. Then m = n√2 and m√2 = 2n.
- We may assume that n is the smallest integer so that n√2 is an integer. That is, that the fraction m/n is in lowest terms.
- Then
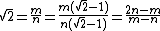
- Because 1 > √2 − 1 > 0, it follows that n > n(√2 − 1) = m − n > 0.
- So the fraction m/n for √2, which according to (2) is already in lowest terms, is represented by (3) in strictly lower terms. This is a contradiction, so the assumption that √2 is rational must be false.
Geometric proof
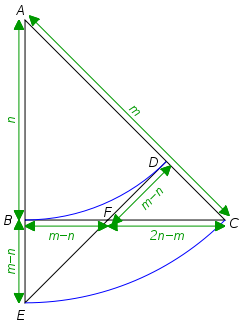
Another reductio ad absurdum
Reductio ad absurdum
In logic, proof by contradiction is a form of proof that establishes the truth or validity of a proposition by showing that the proposition's being false would imply a contradiction...
showing that √2 is irrational is less well-known. It is also an example of proof by infinite descent
Infinite descent
In mathematics, a proof by infinite descent is a particular kind of proof by contradiction which relies on the fact that the natural numbers are well ordered. One typical application is to show that a given equation has no solutions. Assuming a solution exists, one shows that another exists, that...
. It makes use of classic compass and straightedge
Compass and straightedge
Compass-and-straightedge or ruler-and-compass construction is the construction of lengths, angles, and other geometric figures using only an idealized ruler and compass....
construction, proving the theorem by a method similar to that employed by ancient Greek geometers. It is essentially the previous proof viewed geometrically.
Let ABC be a right isosceles triangle with hypotenuse length m and legs n. By the Pythagorean theorem
Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
, m/n = √2. Suppose m and n are integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s. Let m:n be a ratio
Ratio
In mathematics, a ratio is a relationship between two numbers of the same kind , usually expressed as "a to b" or a:b, sometimes expressed arithmetically as a dimensionless quotient of the two which explicitly indicates how many times the first number contains the second In mathematics, a ratio is...
given in its lowest terms.
Draw the arcs BD and CE with centre A. Join DE. It follows that AB = AD, AC = AE and the ∠BAC and ∠DAE coincide. Therefore the triangles ABC and ADE are congruent
Congruence (geometry)
In geometry, two figures are congruent if they have the same shape and size. This means that either object can be repositioned so as to coincide precisely with the other object...
by SAS.
Because ∠EBF is a right angle and ∠BEF is half a right angle, BEF is also a right isosceles triangle. Hence BE = m − n implies BF = m − n. By symmetry, DF = m − n, and FDC is also a right isosceles triangle. It also follows that FC = n − (m − n) = 2n − m.
Hence we have an even smaller right isosceles triangle, with hypotenuse length 2n − m and legs m − n. These values are integers even smaller than m and n and in the same ratio, contradicting the hypothesis that m:n is in lowest terms. Therefore m and n cannot be both integers, hence √2 is irrational.
Analytic proof
- Lemma: let
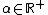 and
and 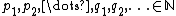 such that
such that 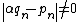 for all
for all 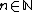 and
and
- Then α is irrational.
Proof: suppose α = a/b with a, b ∈ N+.
For sufficiently big n,
then
but aqn − bpn is an integer, absurd, then α is irrational.
- √2 is irrational.
Proof: let p1 = q1 = 1 and
for all n ∈ N.
By induction
Mathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
,
for all n ∈ N. For n = 1,
and if is true for n then is true for n + 1. In fact
By application of the lemma, √2 is irrational.
Constructive proof
In a constructive proof, one distinguishes between on the one hand not being rational, and on the other hand being irrational (i.e., being quantifiably apart from every rational), the latter being a stronger property. Given integers a and b, because the valuation of 2b2 is odd, while the valuation of a2 is even, they must be distinct integers, so that, applying the law of trichotomy in the context of an effectively computable predicate over N, we obtain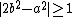 . An easy calculation then yields a lower bound of
. An easy calculation then yields a lower bound of 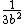 for the difference
for the difference  , yielding a direct proof of irrationality not relying on the law of excluded middle
, yielding a direct proof of irrationality not relying on the law of excluded middleLaw of excluded middle
In logic, the law of excluded middle is the third of the so-called three classic laws of thought. It states that for any proposition, either that proposition is true, or its negation is....
, see Errett Bishop
Errett Bishop
Errett Albert Bishop was an American mathematician known for his work on analysis. He is the father of constructive analysis, because of his 1967 Foundations of Constructive Analysis, where he proved most of the important theorems in real analysis by constructive methods.-Life:Errett Bishop's...
(1985, p. 18).
Properties of the square root of two
One-half of √2, approximately 0.70710 67811 86548, is a common quantity in geometry and trigonometryTrigonometry
Trigonometry is a branch of mathematics that studies triangles and the relationships between their sides and the angles between these sides. Trigonometry defines the trigonometric functions, which describe those relationships and have applicability to cyclical phenomena, such as waves...
because the unit vector that makes a 45° angle with the axes in a plane has the coordinates
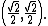
This number satisfies
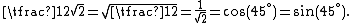
One interesting property of the square root of two is as follows:
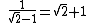
since
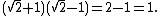 This is related to the property of silver means.
This is related to the property of silver means.The square root of two can also be expressed in terms of the copies of the imaginary unit
Imaginary unit
In mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek...
i using only the square root
Square root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
and arithmetic operations:
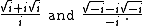
The square root of two is also the only real number other than 1 whose infinite tetrate
Tetration
In mathematics, tetration is an iterated exponential and is the next hyper operator after exponentiation. The word tetration was coined by English mathematician Reuben Louis Goodstein from tetra- and iteration. Tetration is used for the notation of very large numbers...
is equal to its square.

The square root of two appears in Viète's formula for π:
for m square roots and only one minus sign.
It is not known whether √2 is a normal number
Normal number
In mathematics, a normal number is a real number whose infinite sequence of digits in every base b is distributed uniformly in the sense that each of the b digit values has the same natural density 1/b, also all possible b2 pairs of digits are equally likely with density b−2,...
, a stronger property than irrationality, but statistical analyses of its binary expansion are consistent with the hypothesis that it is normal to base two.
Series and product representations
The identity cos(π/4) = sin(π/4) = 1/√2, along with the infinite product representations for the sine and cosine, leads to products such as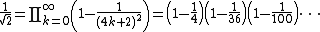
and
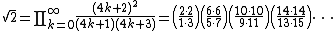
or equivalently,
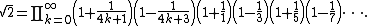
The number can also be expressed by taking the Taylor series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
of a trigonometric function. For example, the series for cos(π/4) gives

The Taylor series of √(1 + x) with x = 1 and using the double factorial n!! gives
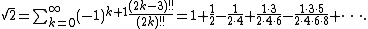
The convergence of this series can be accelerated with an Euler transform, producing
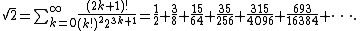
It is not known whether √2 can be represented with a BBP-type formula. BBP-type formulas are known for π√2 and √2 ln(1 + √2), however. http://crd.lbl.gov/~dhbailey/dhbpapers/bbp-formulas.pdf
Continued fraction representation
The square root of two has the following continued fractionContinued fraction
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on...
representation:

The convergents
Convergent (continued fraction)
A convergent is one of a sequence of values obtained by evaluating successive truncations of a continued fraction The nth convergent is also known as the nth approximant of a continued fraction.-Representation of real numbers:...
formed by truncating this representation form a sequence of fractions that approximate the square root of two to increasing accuracy, and that are described by the Pell number
Pell number
In mathematics, the Pell numbers are an infinite sequence of integers that have been known since ancient times, the denominators of the closest rational approximations to the square root of 2. This sequence of approximations begins 1/1, 3/2, 7/5, 17/12, and 41/29, so the sequence of Pell numbers...
s (known as side and diameter numbers to the ancient Greeks because of their use in approximating the ratio between the sides and diagonal of a square). The first convergents are: 1/1, 3/2, 7/5, 17/12, 41/29, 99/70, 239/169, 577/408. The convergent p/q differs from the square root of 2 by almost exactly
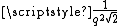 and then the next convergent is (p + 2q)/(p + q).
and then the next convergent is (p + 2q)/(p + q).Paper size
The square root of two is the aspect ratioAspect ratio
The aspect ratio of a shape is the ratio of its longer dimension to its shorter dimension. It may be applied to two characteristic dimensions of a three-dimensional shape, such as the ratio of the longest and shortest axis, or for symmetrical objects that are described by just two measurements,...
of paper size
Paper size
Many paper size standards conventions have existed at different times and in different countries. Today there is one widespread international ISO standard and a localised standard used in North America . The paper sizes affect writing paper, stationery, cards, and some printed documents...
s under ISO 216
ISO 216
ISO 216 specifies international standard paper sizes used in most countries in the world today. It defines the "A" and "B" series of paper sizes, including A4, the most commonly available size...
(A4, A0, etc.). This ratio guarantees that cutting a sheet in half along a line parallel to its short side results in two sheets having the same ratio.
See also
- Pythagoras' constant
- Square root of 3Square root of 3The square root of 3 is the positive real number that, when multiplied by itself, gives the number 3. It is more precisely called the principal square root of 3, to distinguish it from the negative number with the same property...
- Square root of 5
- Silver ratioSilver ratioIn mathematics, two quantities are in the silver ratio if the ratio between the sum of the smaller plus twice the larger of those quantities and the larger one is the same as the ratio between the larger one and the smaller. This defines the silver ratio as an irrational mathematical constant,...
, 1 + √2 - The square root of two is the frequency ratio of a tritoneTritoneIn classical music from Western culture, the tritone |tone]]) is traditionally defined as a musical interval composed of three whole tones. In a chromatic scale, each whole tone can be further divided into two semitones...
interval in twelve-tone equal temperamentEqual temperamentAn equal temperament is a musical temperament, or a system of tuning, in which every pair of adjacent notes has an identical frequency ratio. As pitch is perceived roughly as the logarithm of frequency, this means that the perceived "distance" from every note to its nearest neighbor is the same for...
music. - The square root of two also forms the relationship of f stops in photographic lenses, which in turn means that the ratio of areas between two successive apertureApertureIn optics, an aperture is a hole or an opening through which light travels. More specifically, the aperture of an optical system is the opening that determines the cone angle of a bundle of rays that come to a focus in the image plane. The aperture determines how collimated the admitted rays are,...
s is 2. - Viète's formula
External links
.- The Square Root of Two to 5 million digits by Jerry Bonnell and Robert Nemiroff. May, 1994.
- Square root of 2 is irrational, a collection of proofs
- √2.net, enthusiast site with realtime computation
- Square Root of 2 Search Engine 2 billion searchable digits of √2, and