In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

 and computer science

Computer science

Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...

, an optimization problem is the problem of finding the best solution from all feasible solutions. Optimization problems can be divided into two categories depending on whether the variables

Variable (mathematics)

In mathematics, a variable is a value that may change within the scope of a given problem or set of operations. In contrast, a constant is a value that remains unchanged, though often unknown or undetermined. The concepts of constants and variables are fundamental to many areas of mathematics and...

 are continuous or discrete. An optimization problem with discrete variables is known as a combinatorial optimization problem. In a combinatorial optimization problem, we are looking for an object such as an integer, permutation or graph from a finite (or possibly countable infinite) set.

Continuous optimization problem

The standard form of a (continuous) optimization problem is

where

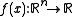• is the objective function to be minimized over the variable ,
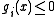• are called inequality constraints, and
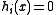• are called equality constraints.

By convention, the standard form defines a minimization problem. A maximization problem can be treated by negating the objective function.

Combinatorial optimization problem

Formally, a combinatorial optimization

Combinatorial optimization

In applied mathematics and theoretical computer science, combinatorial optimization is a topic that consists of finding an optimal object from a finite set of objects. In many such problems, exhaustive search is not feasible...

 problem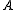 is a quadruple 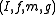, where

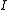• is a set of instances;
• given an instance 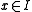, 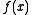is the set of feasible solutions;
• given an instance and a feasible solution 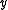of , 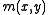denotes the measure of 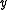, which is usually a positive real.
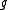• is the goal function, and is eithe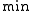r or .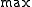

The goal is then to find for some instance an optimal solution, that is, a feasible solution 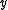with

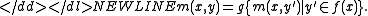
For each combinatorial optimization problem, there is a corresponding decision problem

Decision problem

In computability theory and computational complexity theory, a decision problem is a question in some formal system with a yes-or-no answer, depending on the values of some input parameters. For example, the problem "given two numbers x and y, does x evenly divide y?" is a decision problem...

 that asks whether there is a feasible solution for some particular measure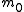 . For example, if there is a graph

Graph (mathematics)

In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...

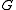  which contains vertices and , an optimization problem might be "find a path from to that uses the fewest edges". This problem might have an answer of, say, 4. A corresponding decision problem would be "is there a path from to that uses 10 or fewer edges?" This problem can be answered with a simple 'yes' or 'no'.

In the field of approximation algorithm

Approximation algorithm

In computer science and operations research, approximation algorithms are algorithms used to find approximate solutions to optimization problems. Approximation algorithms are often associated with NP-hard problems; since it is unlikely that there can ever be efficient polynomial time exact...

s, algorithms are designed to find near-optimal solutions to hard problems. The usual decision version is then an inadequate definition of the problem since it only specifies acceptable solutions. Even though we could introduce suitable decision problems, the problem is more naturally characterized as an optimization problem.

NP optimization problem

An NP-optimization problem (NPO) is a combinatorial optimization problem with the following additional conditions. Note that the below referred polynomials are functions of the size of the respective functions' inputs, not the size of some implicit set of input instances.

• the size of every feasible solution 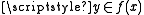is polynomially bounded in the size of the given instance ,
• the languages 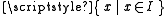and 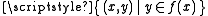can be recognized in polynomial time, and
• m is polynomial-time computable.

This implies that the corresponding decision problem is in NP

NP (complexity)

In computational complexity theory, NP is one of the most fundamental complexity classes.The abbreviation NP refers to "nondeterministic polynomial time."...

. In computer science, interesting optimization problems usually have the above properties and are therefore NPO problems. A problem is additionally called a P-optimization (PO) problem, if there exists an algorithm which finds optimal solutions in polynomial time. Often, when dealing with the class NPO, one is interested in optimization problems for which the decision versions are NP-hard. Note that hardness relations are always with respect to some reduction. Due to the connection between approximation algorithms and computational optimization problems, reductions which preserve approximation in some respect are for this subject preferred than the usual Turing

Turing reduction

In computability theory, a Turing reduction from a problem A to a problem B, named after Alan Turing, is a reduction which solves A, assuming B is already known . It can be understood as an algorithm that could be used to solve A if it had available to it a subroutine for solving B...

 and Karp reductions. An example of such a reduction would be the L-reduction

L-reduction

In computer science, in particular in the study of approximation algorithms, anL-reduction is a transformation of optimization problems which linearly preserves approximability features...

. For this reason, optimization problems with NP-complete decision versions are not necessarily called NPO-complete.

NPO is divided into the following subclasses according to their approximability:

• NPO(I): Equals FPTAS. Contains the Knapsack problem
  Knapsack problem
  The knapsack problem or rucksack problem is a problem in combinatorial optimization: Given a set of items, each with a weight and a value, determine the count of each item to include in a collection so that the total weight is less than or equal to a given limit and the total value is as large as...
  
  .
• NPO(II): Equals PTAS
  Polynomial-time approximation scheme
  In computer science, a polynomial-time approximation scheme is a type of approximation algorithm for optimization problems ....
  
  . Contains the Makespan scheduling problem.
• NPO(III): :The class of NPO problems that have polynomial-time algorithms which computes solutions with a cost at most c times the optimal cost (for minimization problems) or a cost at least 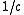of the optimal cost (for maximization problems). In Hromkovič
  Juraj Hromkovic
  Juraj Hromkovič is a Slovak Computer Scientist and Professor at ETH Zürich. He is the author of numerous monographs and scientific publications in the field of algorithmics, computational complexity theory, and randomization.- Biography :...
  
  's book, excluded from this class are all NPO(II)-problems save if P=NP. Without the exclusion, equals APX. Contains MAX-SAT and metric TSP
  Travelling salesman problem
  The travelling salesman problem is an NP-hard problem in combinatorial optimization studied in operations research and theoretical computer science. Given a list of cities and their pairwise distances, the task is to find the shortest possible tour that visits each city exactly once...
  
  .
• NPO(IV): :The class of NPO problems with polynomial-time algorithms approximating the optimal solution by a ratio that is polynomial in a logarithm of the size of the input. In Hromkovic's book, all NPO(III)-problems are excluded from this class unless P=NP. Contains the set cover problem.
• NPO(V): :The class of NPO problems with polynomial-time algorithms approximating the optimal solution by a ratio bounded by some function on n. In Hromkovic's book, all NPO(IV)-problems are excluded from this class unless P=NP. Contains the TSP
  Travelling salesman problem
  The travelling salesman problem is an NP-hard problem in combinatorial optimization studied in operations research and theoretical computer science. Given a list of cities and their pairwise distances, the task is to find the shortest possible tour that visits each city exactly once...
  
   and Max Clique problems
  Clique problem
  In computer science, the clique problem refers to any of the problems related to finding particular complete subgraphs in a graph, i.e., sets of elements where each pair of elements is connected....
  
  .

Another class of interest is NPOPB, NPO with polynomially bounded cost functions. Problems with this condition have many desirable properties.

See also

• Mathematical optimization
• Semi-infinite programming
• Decision problem
  Decision problem
  In computability theory and computational complexity theory, a decision problem is a question in some formal system with a yes-or-no answer, depending on the values of some input parameters. For example, the problem "given two numbers x and y, does x evenly divide y?" is a decision problem...
  
  
• Search problem
  Search problem
  In computational complexity theory and computability theory, a search problem is a type of computational problem represented by a binary relation...
  
  
• Counting problem (complexity)
• Function problem
  Function problem
  In computational complexity theory, a function problem is a computational problem where a single output is expected for every input, but the output is more complex than that of a decision problem, that is, it isn't just YES or NO...
  
  

The source of this article is wikipedia, the free encyclopedia.  The text of this article is licensed under the GFDL.