
Interval finite element
Encyclopedia
The interval finite element method (interval FEM) is a finite element method
that uses interval parameters. Interval FEM can be applied in situations where it is not possible to get reliable probabilistic characteristics of the structure. This is important in concrete structures, wood structures, geomechanics, composite structures, biomechanics and in many other areas http://andrzej.pownuk.com/IntervalEquations.htm. The goal of the Interval Finite Element is to find upper and lower bounds of different characteristics of the model (e.g. stress, displacements
, yield surface
etc.) and use these results in the design process. This is so called worst case design, which is closely related to the limit state design
.
Worst case design require less information than probabilistic design
however the results are more conservative [Köylüoglu and Elishakoff 1998].

where a and b are real number
s is equal to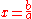 .
.
Very often exact values of the parameters a and b are unknown.
Let's assume that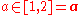 and
and 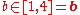 . In that case it is necessary to solve the following equation
. In that case it is necessary to solve the following equation

There are several definition of the solution set of the equation with the interval parameters.
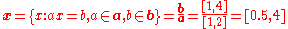
This is the most popular solution set of the interval equation and this solution set will be applied in this article.
In the multidimensional case the united solutions set is much more complicated.
Solution set of the following system of linear interval equations
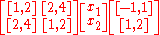
is shown on the following picture
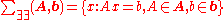
Exact solution set is very complicated, because of that in applications it is necessary to find the smallest interval which contain the exact solution set

or simply

where

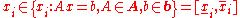
See also http://www.ippt.gov.pl/~kros/pccmm99/01Title.html
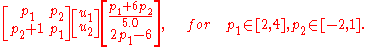
is shown on the picture below (E. Popova, Parametric Solution Set of Interval Linear System http://cose.math.bas.bg/webMathematica/webComputing/ParametricSSet.jsp).
for which the equation

is satisfied. In other words left side of the equation is equal to the right side of the equation.
In this particular case the solution is equal to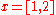 because
because
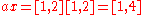
If the uncertainty is bigger i.e.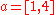 , then
, then 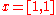 because
because
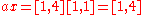
If the uncertainty is even bigger i.e.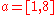 , then the solution doesn't exist. It is really hard to find physical interpretation of the algebraic interval solution set.
, then the solution doesn't exist. It is really hard to find physical interpretation of the algebraic interval solution set.
Because of that in applications usually the united solution set is applied.
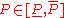 . Mid point value of the load is equal to
. Mid point value of the load is equal to 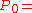 10 [kN].
10 [kN].


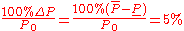
The truss structure contain 69 bars with the length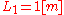 or
or 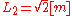 , Young's modulus
, Young's modulus  , area of cross-section
, area of cross-section 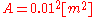
Relative error of the interval axial forces
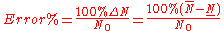
is given in the following table
According to the numerical results the relative error of the axial forces is bigger than 100%, however variations of the forces P are equal to only 5% [Pownuk 2004]. Calculation of the range of function is the main objective of the Interval Finite Element Method. ANSYS input files which can be used to the verification of the results can be found on the following web page http://andrzej.pownuk.com/uncertainty/truss1.htm.
The truss structure contain 15 bars with the length , Young's modulus
, Young's modulus  , area of cross-section
, area of cross-section 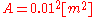 ,
,  . Mid point value of the load is equal to
. Mid point value of the load is equal to  10 [kN].
10 [kN].



Results of the calculations are shown below (compare http://andrzej.pownuk.com/uncertainty/truss2.htm).
Relative error of the interval axial forces.
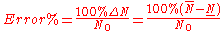
Relative error is bigger than 60%.

where is a vector of parameters which belong to given intervals
is a vector of parameters which belong to given intervals
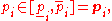

For example the heat transfer eqation
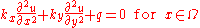

where are the interval parameters (i.e.
are the interval parameters (i.e. 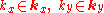 ).
).
Solution of the equation (1) can be defined in the following way
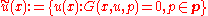
For example in the case of the heat transfer equation
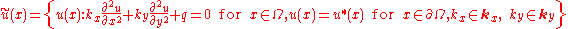
Solution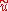 is very complicated because of that in practice it is more interesting to find the smallest possible interval which contain the exact solution set
is very complicated because of that in practice it is more interesting to find the smallest possible interval which contain the exact solution set 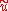 .
.

For example in the case of the heat transfer equation
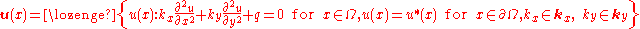
Finite element method lead to the following parameter dependent system of algebraic equations
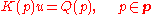
where is a stiffness matrix and
is a stiffness matrix and  is a right hand side.
is a right hand side.
Interval solution can be defined as a multivalued function

In the simplest case above system can be treat as a system of linear interval equations.
It is also possible to define the interval solution as a solution of the following optimization problem
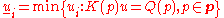
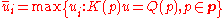
In multidimensional case the intrval solution can be written as

Valliappan S., Pham T.D., 1993, Fuzzy Finite Element Analysis of A Foundation on Elastic Soil Medium. International Journal for Numerical and Analytical Methods in Geomechanics, Vol.17, pp. 771–789
Elishakoff I., Li Y.W., Starnes J.H., 1994, A deterministic method to predict the effect of unknown-but-bounded elastic moduli on the buckling of composite structures. Computer methods in applied mechanics and engineering, Vol.111, pp. 155–167
Valliappan S. Pham T.D., 1995, Elasto-Plastic Finite Element Analysis with Fuzzy Parameters. International Journal for Numerical Methods in Engineering, 38, pp. 531–548
Rao S.S., Sawyer J.P., 1995, Fuzzy Finite Element Approach for the Analysis of Imprecisly Defined Systems. AIAA Journal, Vol.33, No.12, pp. 2364–2370
Köylüoglu H.U., Cakmak A., Nielsen S.R.K., 1995, Interval mapping in structural mechanics. In: Spanos, ed. Computational Stochastic Mechanics. 125-133. Balkema, Rotterdam
Muhanna, R. L. and R. L. Mullen (1995). "Development of Interval Based Methods for Fuzziness in Continuum Mechanics" in Proceedings of the 3rd International Symposium on Uncertainty Modeling and Analysis and Annual Conference of the North American Fuzzy Information Processing Society (ISUMA–NAFIPS'95),IEEE, 705–710
More references can be found here http://andrzej.pownuk.com/IntervalEquations.htm
.
Interval parameter take into account all possible probability distributions (for
take into account all possible probability distributions (for 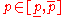 ).
).
In order to define the interval parameter it is necessary to know only upper and lower bound
and lower bound 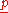 .
.
Calculations of probabilistic characteristics require the knowledge of a lot of experimental results.
It is possible to show that the sum of n interval numbers is times wider than the sum of appropriate normally distributed random variables.
times wider than the sum of appropriate normally distributed random variables.
Sum of n interval number is equal to
is equal to
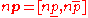
Width of that interval is equal to
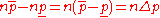
Let us consider normally distributed random variable X such that
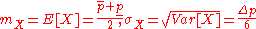
Sum of n normally distributed random variable is a normally distributed random variable with the following characteristics (see Six Sigma
)
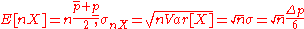
We can assume that the width of the probabilistic result is equal to 6 sigma (compare Six Sigma
).

Now we can compare the width of the interval result and the probabilistic result

Because of that the results of the interval finite element (or in general worst case analysis) may be overestimated in comparison to the stochastic fem analysis (see also propagation of uncertainty
).
However in the case of nonprobabilistic uncertainty it is not possible to apply pure probabilistic methods.
Because probabilistic characteristic in that case are not known exactly [Elishakoff 2000].
It is possible to consider random (and fuzzy random variables) with the interval parameters (e.g. with the interval mean, variance etc.).
Some researchers use interval (fuzzy) measurements in statistical calculations (e.g. http://www.cs.utep.edu/interval-comp/interval.02/fers.pdf). As a results of such calculations we will get so called imprecise probability
.
Imprecise probability
is understood in a very wide sense. It is used as a generic term to cover all mathematical models which measure chance or uncertainty without sharp numerical probabilities. It includes both qualitative (comparative probability, partial preference orderings, …) and quantitative modes (interval probabilities, belief functions, upper and lower previsions, …). Imprecise probability models are needed in inference problems where the relevant information is scarce, vague or conflicting, and in decision problems where preferences may also be incomplete http://www.sipta.org/.

where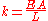 ,
, 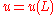 or simply
or simply
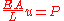
(compare the definition of Young's modulus
).
Let us assume that the Young's modulus and the force are uncertain
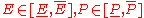
In order to find upper and lower bound of the displacement u it is necessary to calculate partial derivatives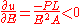

Extreme values of the displacement can be calculated in the following way
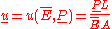
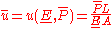
Strain can be calculated from the following formula

Derivative of the strain can be calculated by using derivative from the displacements (the same approach can be applied in more complex problems)
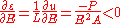
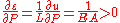
Extreme values of the strains can be calcuated as
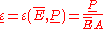
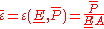
It is also possible to calculate extreme valuse of strain using the displacements

then
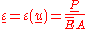
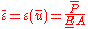
The same methodology can be applied to the stress
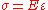
then

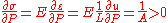
and

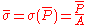
If we treat stress as a function of strain then
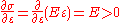
then
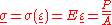
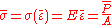
Structure is safe if stress is smaller than a given value
is smaller than a given value 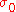 i.e.
i.e.

this condition is true if

After calculation we know that this relation is satisfied if
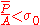
The example is very simple but it shows the applications of the interval parameters in mechanics. Interval FEM use very similar methodology in multidimensional cases [Pownuk 2004].
However in the multidimensional cases relation between the uncertain parameters and the solution is not always monotone. In that cases more complicated optimization methods have to be applied http://andrzej.pownuk.com/IntervalEquations.htm.
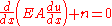
where is displacement,
is displacement,  is Young's modulus
is Young's modulus
, is an area of cross-section, and
is an area of cross-section, and  is a distributed load.
is a distributed load.
In order to get unique solution it is necessary to add appropriate boundary conditions e.g.
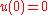
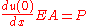
If Young's modulus
 and
and  are uncertain then the interval solution can be defined in the following way
are uncertain then the interval solution can be defined in the following way
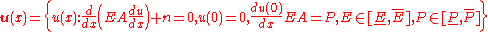
For each FEM element it is possible to multiply the equation by the test function

where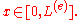
After integration by parts we will get the equation in the week form
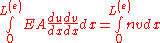
where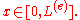
Let's introduce a set of grid points , where
, where  is a number of elements, and linear shape functions for each FEM element
is a number of elements, and linear shape functions for each FEM element
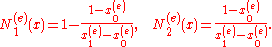
where
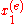 left endpoint of the element,
left endpoint of the element, 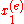 left endpoint of the element number "e".
left endpoint of the element number "e".
Approximate solution in the "e"-th element is a linear combination of the shape functions
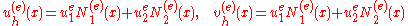
After substitution to the weak form of the equation we will get the following system of equations
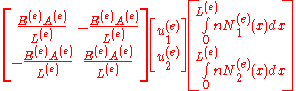
or in the matrix form
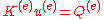
In order to assemble the global stiffness matrix it is necessary to consider an equilibrium equations in each node.
After that the equation has the following matrix form

where
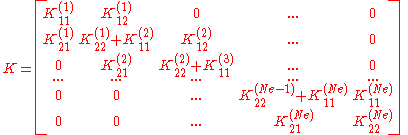
is the global stiffness matrix,
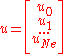
is the solution vector,
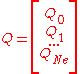
is the right hand side.
In the case of tension-compression problem

If we neglect the distributed load
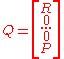
After taking into account the boundary conditions the stiffness matrix has the following form
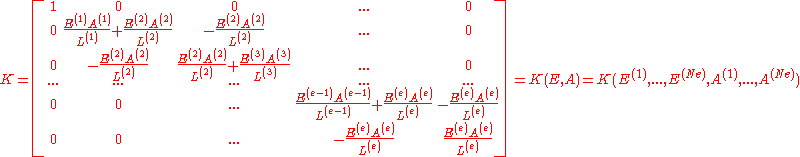
Right-hand side has the following form
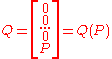
Let's assume that Young's modulus , area of cross-section
, area of cross-section  and the load
and the load 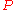 are uncertain and belong to some intervals
are uncertain and belong to some intervals
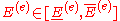

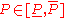
The interval solution can be defined calculating the following way

Calculation of the interval vector is in general NP-hard
is in general NP-hard
, however in specific cases it is possible to calculate the solution which can be used in many engineering applications.
The results of the calculations are the interval displacements
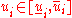
Let's assume that the displacements in the column have to be smaller than some given value (due to safety).
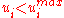
The uncertain system is safe if the interval solution satisfy all safety conditions.
In this particular case

or simple
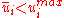
In postprocessing it is possible to calculate the interval stress, the interval strain and the interval limit state functions
and use these values in the design process.
The interval finite element method can be applied to the solution of problems in which there is not enough information to create reliable probabilistic characteristic of the structures [Elishakoff 2000]. Interval finite element method can be also applied in the theory of imprecise probability
.
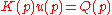 for all possible combinations of endpoints of the interval
for all possible combinations of endpoints of the interval 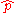 .
.
The list of all vertices of the interval can be written as
can be written as 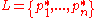 .
.
Upper and lower bound of the solution can be calculated in the following way
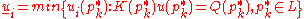
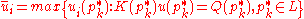
Endpoints combination method gives solution which is usually exact; unfortunately the method has exponential computational complexity and cannot be applied to the problems with many interval parameters [Neumaier 1990].
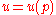 can be expanded by using Taylor series
can be expanded by using Taylor series
.
In the simplest case the Taylor series use only linear approximation
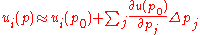
Upper and lower bound of the solution can be calculated by using the following formula
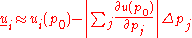
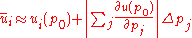
The method is very efficient however it is not very accurate.
In order to improve accuracy it is possible to apply higher order Taylor expansion [Pownuk 2004].
This approach can be also applied in the interval finite difference method and the interval boundary element method
.
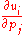 is constant then the functions
is constant then the functions 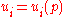 is monotone and the exact solution can be calculated very fast.
is monotone and the exact solution can be calculated very fast.
Extreme values of the solution can be calculated in the following way
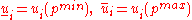
In many structural engineering applications the method gives exact solution.
If the solution is not monotone the solution is usually reasonable. In order to improve accuracy of the method it is possible to apply monotonicity tests and higher order sensitivity analysis. The method can be applied to the solution of linear and nonlinear problems of computational mechanics [Pownuk 2004]. Applications of sensitivity analysis method to the solution of civil engineering problems can be found in the following paper [M.V. Rama Rao, A. Pownuk and I. Skalna 2008].
This approach can be also applied in the interval finite difference method and the interval boundary element method
.
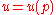 stiffness matrix
stiffness matrix 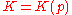 and the load vector
and the load vector  can be expanded by using perturbation theory
can be expanded by using perturbation theory
. Perturbation theory lead to the approximate value of the interval solution [Qiu, Elishakoff 1998]. The method is very efficient and can be applied to large problems of computational mechanics.
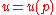 by using response surface. Then it is possible to use the response surface to the get the interval solution [Akpan 2000]. Using response surface method it is possible to solve very complex problem of computational mechanics [Beer 2008].
by using response surface. Then it is possible to use the response surface to the get the interval solution [Akpan 2000]. Using response surface method it is possible to solve very complex problem of computational mechanics [Beer 2008].
Finite element method
The finite element method is a numerical technique for finding approximate solutions of partial differential equations as well as integral equations...
that uses interval parameters. Interval FEM can be applied in situations where it is not possible to get reliable probabilistic characteristics of the structure. This is important in concrete structures, wood structures, geomechanics, composite structures, biomechanics and in many other areas http://andrzej.pownuk.com/IntervalEquations.htm. The goal of the Interval Finite Element is to find upper and lower bounds of different characteristics of the model (e.g. stress, displacements
Displacement (vector)
A displacement is the shortest distance from the initial to the final position of a point P. Thus, it is the length of an imaginary straight path, typically distinct from the path actually travelled by P...
, yield surface
Yield surface
A yield surface is a five-dimensional surface in the six-dimensional space of stresses. The yield surface is usually convex and the state of stress of inside the yield surface is elastic. When the stress state lies on the surface the material is said to have reached its yield point and the...
etc.) and use these results in the design process. This is so called worst case design, which is closely related to the limit state design
Limit state design
Limit state design refers to a design method used in structural engineering. A limit state is a condition of a structure beyond which it no longer fulfills the relevant design criteria. The condition may refer to a degree of loading or other actions on the structure, while the criteria refers to...
.
Worst case design require less information than probabilistic design
Probabilistic design
Probabilistic design is a discipline within engineering design. It deals primarily with the consideration of the effects of random variability upon the performance of an engineering system during the design phase. Typically, these effects are related to quality and reliability...
however the results are more conservative [Köylüoglu and Elishakoff 1998].
Applications of the interval parameters to the modeling of uncertainty
Solution of the following equation
where a and b are real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s is equal to
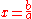 .
.Very often exact values of the parameters a and b are unknown.
Let's assume that
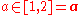 and
and 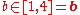 . In that case it is necessary to solve the following equation
. In that case it is necessary to solve the following equation
There are several definition of the solution set of the equation with the interval parameters.
United solution set
In this approach the solution is the following set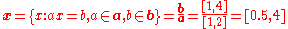
This is the most popular solution set of the interval equation and this solution set will be applied in this article.
In the multidimensional case the united solutions set is much more complicated.
Solution set of the following system of linear interval equations
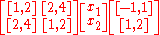
is shown on the following picture
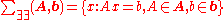
Exact solution set is very complicated, because of that in applications it is necessary to find the smallest interval which contain the exact solution set

or simply

where

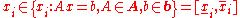
See also http://www.ippt.gov.pl/~kros/pccmm99/01Title.html
Parametric solution set of interval linear system
Interval Finite Element Method require the solution of parameter dependent system of equations (usually with symmetric positive definite matrix). Example of the solution set of general parameter dependent system of equations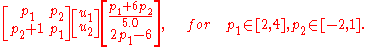
is shown on the picture below (E. Popova, Parametric Solution Set of Interval Linear System http://cose.math.bas.bg/webMathematica/webComputing/ParametricSSet.jsp).
Algebraic solution
In this approach x is such interval numberInterval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
for which the equation

is satisfied. In other words left side of the equation is equal to the right side of the equation.
In this particular case the solution is equal to
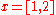 because
because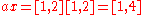
If the uncertainty is bigger i.e.
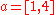 , then
, then 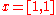 because
because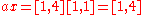
If the uncertainty is even bigger i.e.
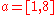 , then the solution doesn't exist. It is really hard to find physical interpretation of the algebraic interval solution set.
, then the solution doesn't exist. It is really hard to find physical interpretation of the algebraic interval solution set.Because of that in applications usually the united solution set is applied.
Example 1
Let us consider a truss structure with uncertain load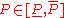 . Mid point value of the load is equal to
. Mid point value of the load is equal to 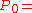 10 [kN].
10 [kN].

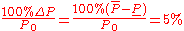
The truss structure contain 69 bars with the length
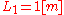 or
or 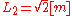 , Young's modulus
, Young's modulus  , area of cross-section
, area of cross-section 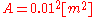
Relative error of the interval axial forces
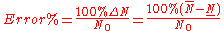
is given in the following table
According to the numerical results the relative error of the axial forces is bigger than 100%, however variations of the forces P are equal to only 5% [Pownuk 2004]. Calculation of the range of function is the main objective of the Interval Finite Element Method. ANSYS input files which can be used to the verification of the results can be found on the following web page http://andrzej.pownuk.com/uncertainty/truss1.htm.
Example 2
Let us consider a truss structure which is shown below.The truss structure contain 15 bars with the length
 , Young's modulus
, Young's modulus  , area of cross-section
, area of cross-section 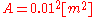 ,
, 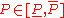 . Mid point value of the load is equal to
. Mid point value of the load is equal to 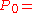 10 [kN].
10 [kN].


Results of the calculations are shown below (compare http://andrzej.pownuk.com/uncertainty/truss2.htm).
Relative error of the interval axial forces.
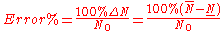
Relative error is bigger than 60%.
The method
Consider PDE with the interval parameters
where
 is a vector of parameters which belong to given intervals
is a vector of parameters which belong to given intervals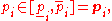

For example the heat transfer eqation
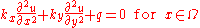

where
 are the interval parameters (i.e.
are the interval parameters (i.e. 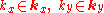 ).
).Solution of the equation (1) can be defined in the following way
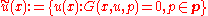
For example in the case of the heat transfer equation
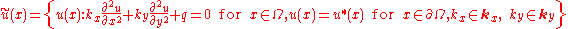
Solution
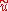 is very complicated because of that in practice it is more interesting to find the smallest possible interval which contain the exact solution set
is very complicated because of that in practice it is more interesting to find the smallest possible interval which contain the exact solution set 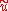 .
.
For example in the case of the heat transfer equation
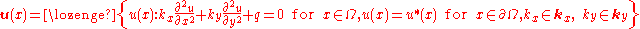
Finite element method lead to the following parameter dependent system of algebraic equations
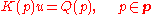
where
 is a stiffness matrix and
is a stiffness matrix and  is a right hand side.
is a right hand side.Interval solution can be defined as a multivalued function

In the simplest case above system can be treat as a system of linear interval equations.
It is also possible to define the interval solution as a solution of the following optimization problem
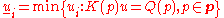
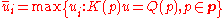
In multidimensional case the intrval solution can be written as

History
Ben-Haim Y., Elishakoff I., 1990, Convex Models of Uncertainty in Applied Mechanics. Elsevier Science Publishers, New YorkValliappan S., Pham T.D., 1993, Fuzzy Finite Element Analysis of A Foundation on Elastic Soil Medium. International Journal for Numerical and Analytical Methods in Geomechanics, Vol.17, pp. 771–789
Elishakoff I., Li Y.W., Starnes J.H., 1994, A deterministic method to predict the effect of unknown-but-bounded elastic moduli on the buckling of composite structures. Computer methods in applied mechanics and engineering, Vol.111, pp. 155–167
Valliappan S. Pham T.D., 1995, Elasto-Plastic Finite Element Analysis with Fuzzy Parameters. International Journal for Numerical Methods in Engineering, 38, pp. 531–548
Rao S.S., Sawyer J.P., 1995, Fuzzy Finite Element Approach for the Analysis of Imprecisly Defined Systems. AIAA Journal, Vol.33, No.12, pp. 2364–2370
Köylüoglu H.U., Cakmak A., Nielsen S.R.K., 1995, Interval mapping in structural mechanics. In: Spanos, ed. Computational Stochastic Mechanics. 125-133. Balkema, Rotterdam
Muhanna, R. L. and R. L. Mullen (1995). "Development of Interval Based Methods for Fuzziness in Continuum Mechanics" in Proceedings of the 3rd International Symposium on Uncertainty Modeling and Analysis and Annual Conference of the North American Fuzzy Information Processing Society (ISUMA–NAFIPS'95),IEEE, 705–710
More references can be found here http://andrzej.pownuk.com/IntervalEquations.htm
Interval solution versus probabilistic solution
It is important to know that the interval parameters generate different results than uniformly distributed random variablesUniform distribution (continuous)
In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by...
.
Interval parameter
 take into account all possible probability distributions (for
take into account all possible probability distributions (for 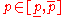 ).
).In order to define the interval parameter it is necessary to know only upper
 and lower bound
and lower bound 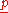 .
.Calculations of probabilistic characteristics require the knowledge of a lot of experimental results.
It is possible to show that the sum of n interval numbers is
 times wider than the sum of appropriate normally distributed random variables.
times wider than the sum of appropriate normally distributed random variables.Sum of n interval number
 is equal to
is equal to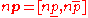
Width of that interval is equal to
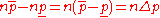
Let us consider normally distributed random variable X such that
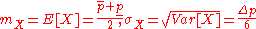
Sum of n normally distributed random variable is a normally distributed random variable with the following characteristics (see Six Sigma
Six Sigma
Six Sigma is a business management strategy originally developed by Motorola, USA in 1986. , it is widely used in many sectors of industry.Six Sigma seeks to improve the quality of process outputs by identifying and removing the causes of defects and minimizing variability in manufacturing and...
)
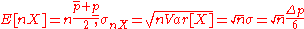
We can assume that the width of the probabilistic result is equal to 6 sigma (compare Six Sigma
Six Sigma
Six Sigma is a business management strategy originally developed by Motorola, USA in 1986. , it is widely used in many sectors of industry.Six Sigma seeks to improve the quality of process outputs by identifying and removing the causes of defects and minimizing variability in manufacturing and...
).

Now we can compare the width of the interval result and the probabilistic result

Because of that the results of the interval finite element (or in general worst case analysis) may be overestimated in comparison to the stochastic fem analysis (see also propagation of uncertainty
Propagation of uncertainty
In statistics, propagation of error is the effect of variables' uncertainties on the uncertainty of a function based on them...
).
However in the case of nonprobabilistic uncertainty it is not possible to apply pure probabilistic methods.
Because probabilistic characteristic in that case are not known exactly [Elishakoff 2000].
It is possible to consider random (and fuzzy random variables) with the interval parameters (e.g. with the interval mean, variance etc.).
Some researchers use interval (fuzzy) measurements in statistical calculations (e.g. http://www.cs.utep.edu/interval-comp/interval.02/fers.pdf). As a results of such calculations we will get so called imprecise probability
Imprecise probability
Imprecise probability generalizes probability theory to allow for partial probability specifications, and is applicable when information is scarce, vague, or conflicting, in which case a unique probability distribution may be hard to identify...
.
Imprecise probability
Imprecise probability
Imprecise probability generalizes probability theory to allow for partial probability specifications, and is applicable when information is scarce, vague, or conflicting, in which case a unique probability distribution may be hard to identify...
is understood in a very wide sense. It is used as a generic term to cover all mathematical models which measure chance or uncertainty without sharp numerical probabilities. It includes both qualitative (comparative probability, partial preference orderings, …) and quantitative modes (interval probabilities, belief functions, upper and lower previsions, …). Imprecise probability models are needed in inference problems where the relevant information is scarce, vague or conflicting, and in decision problems where preferences may also be incomplete http://www.sipta.org/.
1D Example
In the tension-compression problem the relation between the displacement u and the force P is the following
where
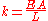 ,
, 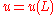 or simply
or simply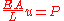
(compare the definition of Young's modulus
Young's modulus
Young's modulus is a measure of the stiffness of an elastic material and is a quantity used to characterize materials. It is defined as the ratio of the uniaxial stress over the uniaxial strain in the range of stress in which Hooke's Law holds. In solid mechanics, the slope of the stress-strain...
).
Let us assume that the Young's modulus and the force are uncertain
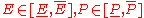
In order to find upper and lower bound of the displacement u it is necessary to calculate partial derivatives
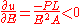

Extreme values of the displacement can be calculated in the following way
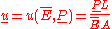
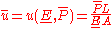
Strain can be calculated from the following formula

Derivative of the strain can be calculated by using derivative from the displacements (the same approach can be applied in more complex problems)
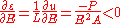
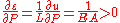
Extreme values of the strains can be calcuated as
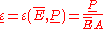
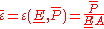
It is also possible to calculate extreme valuse of strain using the displacements

then
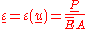
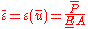
The same methodology can be applied to the stress
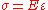
then

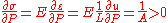
and

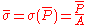
If we treat stress as a function of strain then
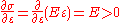
then
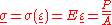
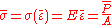
Structure is safe if stress
 is smaller than a given value
is smaller than a given value 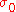 i.e.
i.e.
this condition is true if

After calculation we know that this relation is satisfied if
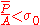
The example is very simple but it shows the applications of the interval parameters in mechanics. Interval FEM use very similar methodology in multidimensional cases [Pownuk 2004].
However in the multidimensional cases relation between the uncertain parameters and the solution is not always monotone. In that cases more complicated optimization methods have to be applied http://andrzej.pownuk.com/IntervalEquations.htm.
Multidimensional example
In the case of tension-compression problem the equilibrium equation has the following form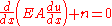
where
 is displacement,
is displacement,  is Young's modulus
is Young's modulusYoung's modulus
Young's modulus is a measure of the stiffness of an elastic material and is a quantity used to characterize materials. It is defined as the ratio of the uniaxial stress over the uniaxial strain in the range of stress in which Hooke's Law holds. In solid mechanics, the slope of the stress-strain...
,
 is an area of cross-section, and
is an area of cross-section, and  is a distributed load.
is a distributed load.In order to get unique solution it is necessary to add appropriate boundary conditions e.g.
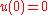
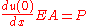
If Young's modulus
Young's modulus
Young's modulus is a measure of the stiffness of an elastic material and is a quantity used to characterize materials. It is defined as the ratio of the uniaxial stress over the uniaxial strain in the range of stress in which Hooke's Law holds. In solid mechanics, the slope of the stress-strain...
 and
and  are uncertain then the interval solution can be defined in the following way
are uncertain then the interval solution can be defined in the following way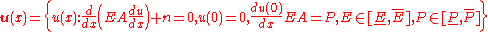
For each FEM element it is possible to multiply the equation by the test function


where
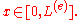
After integration by parts we will get the equation in the week form
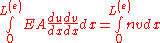
where
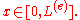
Let's introduce a set of grid points
 , where
, where  is a number of elements, and linear shape functions for each FEM element
is a number of elements, and linear shape functions for each FEM element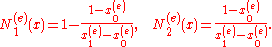
where

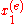 left endpoint of the element,
left endpoint of the element, 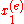 left endpoint of the element number "e".
left endpoint of the element number "e".Approximate solution in the "e"-th element is a linear combination of the shape functions
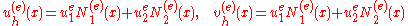
After substitution to the weak form of the equation we will get the following system of equations
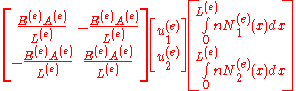
or in the matrix form
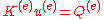
In order to assemble the global stiffness matrix it is necessary to consider an equilibrium equations in each node.
After that the equation has the following matrix form

where
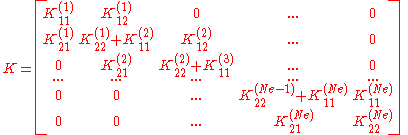
is the global stiffness matrix,
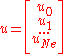
is the solution vector,
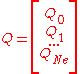
is the right hand side.
In the case of tension-compression problem

If we neglect the distributed load

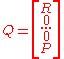
After taking into account the boundary conditions the stiffness matrix has the following form
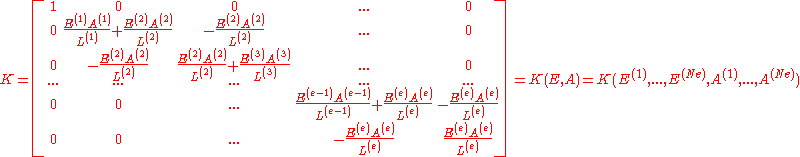
Right-hand side has the following form
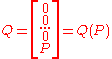
Let's assume that Young's modulus
 , area of cross-section
, area of cross-section  and the load
and the load 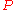 are uncertain and belong to some intervals
are uncertain and belong to some intervals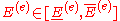

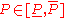
The interval solution can be defined calculating the following way

Calculation of the interval vector
 is in general NP-hard
is in general NP-hardNP-hard
NP-hard , in computational complexity theory, is a class of problems that are, informally, "at least as hard as the hardest problems in NP". A problem H is NP-hard if and only if there is an NP-complete problem L that is polynomial time Turing-reducible to H...
, however in specific cases it is possible to calculate the solution which can be used in many engineering applications.
The results of the calculations are the interval displacements
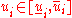
Let's assume that the displacements in the column have to be smaller than some given value (due to safety).
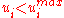
The uncertain system is safe if the interval solution satisfy all safety conditions.
In this particular case

or simple
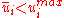
In postprocessing it is possible to calculate the interval stress, the interval strain and the interval limit state functions
Yield surface
A yield surface is a five-dimensional surface in the six-dimensional space of stresses. The yield surface is usually convex and the state of stress of inside the yield surface is elastic. When the stress state lies on the surface the material is said to have reached its yield point and the...
and use these values in the design process.
The interval finite element method can be applied to the solution of problems in which there is not enough information to create reliable probabilistic characteristic of the structures [Elishakoff 2000]. Interval finite element method can be also applied in the theory of imprecise probability
Imprecise probability
Imprecise probability generalizes probability theory to allow for partial probability specifications, and is applicable when information is scarce, vague, or conflicting, in which case a unique probability distribution may be hard to identify...
.
Endpoints combination method
It is possible to solve the equation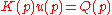 for all possible combinations of endpoints of the interval
for all possible combinations of endpoints of the interval 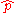 .
. The list of all vertices of the interval
 can be written as
can be written as 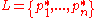 .
. Upper and lower bound of the solution can be calculated in the following way
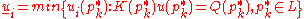
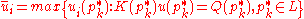
Endpoints combination method gives solution which is usually exact; unfortunately the method has exponential computational complexity and cannot be applied to the problems with many interval parameters [Neumaier 1990].
Taylor expansion method
The function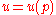 can be expanded by using Taylor series
can be expanded by using Taylor seriesTaylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
.
In the simplest case the Taylor series use only linear approximation
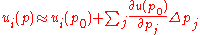
Upper and lower bound of the solution can be calculated by using the following formula
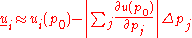
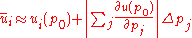
The method is very efficient however it is not very accurate.
In order to improve accuracy it is possible to apply higher order Taylor expansion [Pownuk 2004].
This approach can be also applied in the interval finite difference method and the interval boundary element method
Interval boundary element method
Interval boundary element method is classical boundary element method with the interval parameters.Boundary element method is based on the following integral equation...
.
Gradient method
If the sign of the derivatives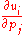 is constant then the functions
is constant then the functions 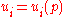 is monotone and the exact solution can be calculated very fast.
is monotone and the exact solution can be calculated very fast.- if
 then
then 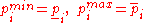
- if
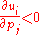 then
then 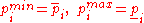
Extreme values of the solution can be calculated in the following way
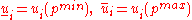
In many structural engineering applications the method gives exact solution.
If the solution is not monotone the solution is usually reasonable. In order to improve accuracy of the method it is possible to apply monotonicity tests and higher order sensitivity analysis. The method can be applied to the solution of linear and nonlinear problems of computational mechanics [Pownuk 2004]. Applications of sensitivity analysis method to the solution of civil engineering problems can be found in the following paper [M.V. Rama Rao, A. Pownuk and I. Skalna 2008].
This approach can be also applied in the interval finite difference method and the interval boundary element method
Interval boundary element method
Interval boundary element method is classical boundary element method with the interval parameters.Boundary element method is based on the following integral equation...
.
Element by element method
Muhanna and Mullen applied element by element formulation to the solution of finite element equation with the interval parameters [Muhanna, Mullen 2001]. Using that method it is possible to get the solution with guaranteed accuracy in the case of truss and frame structures.Perturbation methods
The solution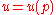 stiffness matrix
stiffness matrix 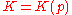 and the load vector
and the load vector  can be expanded by using perturbation theory
can be expanded by using perturbation theoryPerturbation theory
Perturbation theory comprises mathematical methods that are used to find an approximate solution to a problem which cannot be solved exactly, by starting from the exact solution of a related problem...
. Perturbation theory lead to the approximate value of the interval solution [Qiu, Elishakoff 1998]. The method is very efficient and can be applied to large problems of computational mechanics.
Response surface method
It is possible to approximate the solution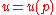 by using response surface. Then it is possible to use the response surface to the get the interval solution [Akpan 2000]. Using response surface method it is possible to solve very complex problem of computational mechanics [Beer 2008].
by using response surface. Then it is possible to use the response surface to the get the interval solution [Akpan 2000]. Using response surface method it is possible to solve very complex problem of computational mechanics [Beer 2008].Pure interval methods
Several authors tried to apply pure interval methods to the solution of finite element problems with the interval parameters. In some cases it is possible to get very interesting results e.g. [Popova, Iankov, Bonev 2008]. However in general the method generates very overestimated results [Kulpa, Pownuk, Skalna 1998].Parametric interval systems
[Popova 2001] and [Skalna 2006] introduced the methods for the solution of the system of linear equations in which the coefficients are linear combinations of interval parameters. In this case it is possible to get very accurate solution of the interval equations with guaranteed accuracy.See also
- Interval boundary element methodInterval boundary element methodInterval boundary element method is classical boundary element method with the interval parameters.Boundary element method is based on the following integral equation...
- Interval (mathematics)Interval (mathematics)In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
- Interval arithmeticInterval arithmeticInterval arithmetic, interval mathematics, interval analysis, or interval computation, is a method developed by mathematicians since the 1950s and 1960s as an approach to putting bounds on rounding errors and measurement errors in mathematical computation and thus developing numerical methods that...
- Imprecise probabilityImprecise probabilityImprecise probability generalizes probability theory to allow for partial probability specifications, and is applicable when information is scarce, vague, or conflicting, in which case a unique probability distribution may be hard to identify...
- Multivalued functionMultivalued functionIn mathematics, a multivalued function is a left-total relation; i.e. every input is associated with one or more outputs...
- Differential inclusion
- Observational errorObservational errorObservational error is the difference between a measured value of quantity and its true value. In statistics, an error is not a "mistake". Variability is an inherent part of things being measured and of the measurement process.-Science and experiments:...
- Random compact setRandom compact setIn mathematics, a random compact set is essentially a compact set-valued random variable. Random compact sets are useful in the study of attractors for random dynamical systems.-Definition:...
- Reliability (statistics)Reliability (statistics)In statistics, reliability is the consistency of a set of measurements or of a measuring instrument, often used to describe a test. Reliability is inversely related to random error.-Types:There are several general classes of reliability estimates:...
- Confidence intervalConfidence intervalIn statistics, a confidence interval is a particular kind of interval estimate of a population parameter and is used to indicate the reliability of an estimate. It is an observed interval , in principle different from sample to sample, that frequently includes the parameter of interest, if the...
- Best, worst and average caseBest, worst and average caseIn computer science, best, worst and average cases of a given algorithm express what the resource usage is at least, at most and on average, respectively...
- Probabilistic designProbabilistic designProbabilistic design is a discipline within engineering design. It deals primarily with the consideration of the effects of random variability upon the performance of an engineering system during the design phase. Typically, these effects are related to quality and reliability...
- Propagation of uncertaintyPropagation of uncertaintyIn statistics, propagation of error is the effect of variables' uncertainties on the uncertainty of a function based on them...
- Experimental uncertainty analysisExperimental uncertainty analysisThe purpose of this introductory article is to discuss the experimental uncertainty analysis of a derived quantity, based on the uncertainties in the experimentally measured quantities that are used in some form of mathematical relationship to calculate that derived quantity...
- Sensitivity analysisSensitivity analysisSensitivity analysis is the study of how the variation in the output of a statistical model can be attributed to different variations in the inputs of the model. Put another way, it is a technique for systematically changing variables in a model to determine the effects of such changes.In any...
- Perturbation theoryPerturbation theoryPerturbation theory comprises mathematical methods that are used to find an approximate solution to a problem which cannot be solved exactly, by starting from the exact solution of a related problem...
- Continuum mechanicsContinuum mechanicsContinuum mechanics is a branch of mechanics that deals with the analysis of the kinematics and the mechanical behavior of materials modelled as a continuous mass rather than as discrete particles...
- Solid mechanicsSolid mechanicsSolid mechanics is the branch of mechanics, physics, and mathematics that concerns the behavior of solid matter under external actions . It is part of a broader study known as continuum mechanics. One of the most common practical applications of solid mechanics is the Euler-Bernoulli beam equation...
- TrussTrussIn architecture and structural engineering, a truss is a structure comprising one or more triangular units constructed with straight members whose ends are connected at joints referred to as nodes. External forces and reactions to those forces are considered to act only at the nodes and result in...
- Space frameSpace frameA space frame or space structure is a truss-like, lightweight rigid structure constructed from interlocking struts in a geometric pattern. Space frames can be used to span large areas with few interior supports...
- Linear elasticityLinear elasticityLinear elasticity is the mathematical study of how solid objects deform and become internally stressed due to prescribed loading conditions. Linear elasticity models materials as continua. Linear elasticity is a simplification of the more general nonlinear theory of elasticity and is a branch of...
- Strength of materialsStrength of materialsIn materials science, the strength of a material is its ability to withstand an applied stress without failure. The applied stress may be tensile, compressive, or shear. Strength of materials is a subject which deals with loads, deformations and the forces acting on a material. A load applied to a...
External links
- http://www.gtsav.gatech.edu/rec/ -- Reliable Engineering Computing, Georgia Institute of Technology, Savannah, USA
- http://www.cs.utep.edu/interval-comp/ -- Interval Computations
- http://www.springerlink.com/content/102987/ -- Reliable Computing (Journal)
- http://andrzej.pownuk.com/IntervalEquations.htm -- Interval equations (collections of references)
- http://andrzej.pownuk.com/interval_web_applications.htm -- Interval finite element web applications
- http://cose.math.bas.bg/webMathematica/webComputing/ParametricSSet.jsp -- E. Popova, Parametric Solution Set of Interval Linear System
- http://www.sipta.org/ -- The Society for Imprecise Probability: Theories and Applications

