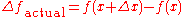Trust region
Encyclopedia
Trust region is a term used in mathematical optimization
to denote the subset of the region of the objective function to be optimized that is approximated using a model function (often a quadratic
). If an adequate model of the objective function is found within the trust region then the region is expanded; conversely, if the approximation is poor then the region is contracted. Trust region methods are also known as restricted step methods.
The fit is evaluated by comparing the ratio of expected improvement from the model approximation with the actual improvement observed in the objective function. Simple thresholding of the ratio is used as the criteria for expansion and contraction—a model function is "trusted" only in the region where it provides a reasonable approximation.
Trust region methods are in some sense dual to line search methods: trust region methods first choose a step size (the size of the trust region) and then a step direction while line search methods first choose a step direction and then a step size.
The term was coined by Celis, Dennis
, and Tapia
at Rice University
.
for 
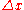, it solves 
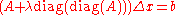where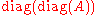 
is the diagonal matrix with the same diagonal as A and λ is a parameter that controls the trust-region size. Geometrically, this adds a parabaloid centered at 
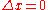to the quadratic form
, resulting in a smaller step.
The trick is to change the trust-region size (λ). At each iteration, the damped quadratic fit predicts a certain reduction in the cost function,
, which we would expect to be a smaller reduction than the true reduction. Given 
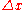we can evaluate
By looking at the ratio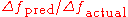
we can adjust the trust-region size. In general, we expect 
to be a bit less than 
and so the ratio would be between, say, 0.25 and 0.5. If the ratio is more than 0.5, then we aren't damping the step much, so expand the trust region (decrease λ), and iterate. If the ratio is smaller than 0.25, then the true function is diverging "too much" from the trust-region approximation, so shrink the trust region (increase λ) and try again.
Optimization (mathematics)
In mathematics, computational science, or management science, mathematical optimization refers to the selection of a best element from some set of available alternatives....
to denote the subset of the region of the objective function to be optimized that is approximated using a model function (often a quadratic
Quadratic
In mathematics, the term quadratic describes something that pertains to squares, to the operation of squaring, to terms of the second degree, or equations or formulas that involve such terms...
). If an adequate model of the objective function is found within the trust region then the region is expanded; conversely, if the approximation is poor then the region is contracted. Trust region methods are also known as restricted step methods.
The fit is evaluated by comparing the ratio of expected improvement from the model approximation with the actual improvement observed in the objective function. Simple thresholding of the ratio is used as the criteria for expansion and contraction—a model function is "trusted" only in the region where it provides a reasonable approximation.
Trust region methods are in some sense dual to line search methods: trust region methods first choose a step size (the size of the trust region) and then a step direction while line search methods first choose a step direction and then a step size.
The term was coined by Celis, Dennis
John E. Dennis
John Emory Dennis, Jr. , is a renowned American mathematician with major contributions in mathematical optimization. Dennis is currently a Noah Harding Professor Emeritus and Research Professor in the Department of Computational and Applied Mathematics at Rice University in Houston, Texas...
, and Tapia
Richard A. Tapia
Richard Alfred Tapia is a renowned American mathematician and champion of under-represented minorities in the sciences. In recognition of his broad contributions, in 2005, Tapia was named "University Professor" at Rice University in Houston, Texas, the University's highest academic title...
at Rice University
Rice University
William Marsh Rice University, commonly referred to as Rice University or Rice, is a private research university located on a heavily wooded campus in Houston, Texas, United States...
.
Example
Conceptually, in the Levenberg–Marquardt algorithm, the objective function is iteratively approximated by a quadratic surface, then using a linear solve, the estimate is updated. This alone may not converge nicely if the initial guess is too far from the optimum. For this reason, the algorithm instead restricts each step, preventing it from stepping "too far". It operationalizes "too far" as follows. 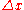Rather than solving for , it solves 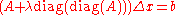where 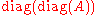is the diagonal matrix with the same diagonal as A and λ is a parameter that controls the trust-region size. Geometrically, this adds a parabaloid centered at 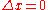to the quadratic formQuadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
, resulting in a smaller step.
The trick is to change the trust-region size (λ). At each iteration, the damped quadratic fit predicts a certain reduction in the cost function,
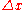, which we would expect to be a smaller reduction than the true reduction. Given we can evaluate
By looking at the ratio
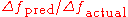we can adjust the trust-region size. In general, we expect to be a bit less than and so the ratio would be between, say, 0.25 and 0.5. If the ratio is more than 0.5, then we aren't damping the step much, so expand the trust region (decrease λ), and iterate. If the ratio is smaller than 0.25, then the true function is diverging "too much" from the trust-region approximation, so shrink the trust region (increase λ) and try again.