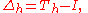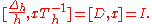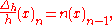Finite difference
Encyclopedia
A finite difference is a mathematical expression of the form f(x + b) − f(x + a). If a finite difference is divided by b − a, one gets a difference quotient
. The approximation of derivatives by finite differences plays a central role in finite difference method
s for the numerical
solution of differential equation
s, especially boundary value problem
s.
Recurrence relation
s can be written as difference equations by replacing iteration notation with finite differences.
A forward difference is an expression of the form
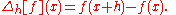
Depending on the application, the spacing h may be variable or constant.
A backward difference uses the function values at x and x − h, instead of the values at x + h and x:
Finally, the central difference is given by
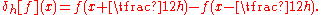
of a function f at a point x is defined by the limit
If h has a fixed (non-zero) value, instead of approaching zero, then the right-hand side is
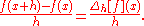
Hence, the forward difference divided by h approximates the derivative when h is small. The error in this approximation can be derived from Taylor's theorem
. Assuming that f is continuously differentiable, the error is
The same formula holds for the backward difference:
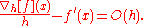
However, the central difference yields a more accurate approximation. Its error is proportional to square of the spacing (if f is twice continuously differentiable):
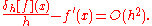
The main problem with the central difference method, however, is that oscillating functions can yield zero derivative. If f(nh)=1 for n uneven, and f(nh)=2 for n even, then f'(nh)=0 if it is calculated with the central difference scheme. This is particularly troublesome if the domain of f is discrete.
In an analogous way one can obtain finite difference approximations to higher order derivatives and differential operators. For example, by using the above central difference formula for
and 
and 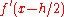applying a central difference formula for the derivative of 
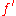at x, we obtain the central difference approximation of the second derivative of f:
2nd Order Central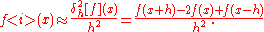
Similarly we can apply other differencing formulas in a recursive manner.
2nd Order Forward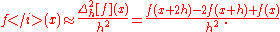
More generally, the nth-order forward, backward, and central differences are respectively given by:
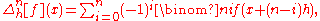
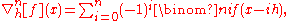
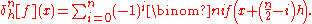
Note that the central difference will, for odd
, have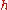 
multiplied by non-integers. This is often a problem because it amounts to changing the interval of discretization. The problem may be remedied taking the average of 
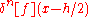and 
.
The relationship of these higher-order differences with the respective derivatives is very straightforward:
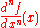
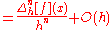
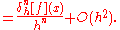
Higher-order differences can also be used to construct better approximations. As mentioned above, the first-order difference approximates the first-order derivative up to a term of order h. However, the combination
approximates f(x) up to a term of order h2. This can be proven by expanding the above expression in Taylor series
, or by using the calculus of finite differences, explained below.
If necessary, the finite difference can be centered about any point by mixing forward, backward, and central differences.
This is useful for differentiating a function on a grid, where, as one approaches the edge of the grid, one must sample fewer and fewer points on one side.
The details are outlined in these notes.
, especially in numerical differential equations
, which aim at the numerical solution of ordinary
and partial differential equation
s respectively. The idea is to replace the derivatives appearing in the differential equation by finite differences that approximate them. The resulting methods are called finite difference method
s.
Common applications of the finite difference method are in computational science and engineering disciplines, such as thermal engineering
, fluid mechanics
, etc.
where
is the binomial coefficient
. Forward differences applied to a sequence
are sometimes called the binomial transform of the sequence, and have a number of interesting combinatorial properties.
Forward differences may be evaluated using the Nörlund–Rice integral. The integral representation for these types of series is interesting because the integral can often be evaluated using asymptotic expansion
or saddle-point techniques; by contrast, the forward difference series can be extremely hard to evaluate numerically, because the binomial coefficients grow rapidly for large n.
; in essence, it is the Newton interpolation formula, first published in his Principia Mathematica in 1687, namely the discrete analog of the continuum Taylor expansion,
Difference quotient
The primary vehicle of calculus and other higher mathematics is the function. Its "input value" is its argument, usually a point expressible on a graph...
. The approximation of derivatives by finite differences plays a central role in finite difference method
Finite difference method
In mathematics, finite-difference methods are numerical methods for approximating the solutions to differential equations using finite difference equations to approximate derivatives.- Derivation from Taylor's polynomial :...
s for the numerical
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
solution of differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
s, especially boundary value problem
Boundary value problem
In mathematics, in the field of differential equations, a boundary value problem is a differential equation together with a set of additional restraints, called the boundary conditions...
s.
Recurrence relation
Recurrence relation
In mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....
s can be written as difference equations by replacing iteration notation with finite differences.
Forward, backward, and central differences
Only three forms are commonly considered: forward, backward, and central differences.A forward difference is an expression of the form
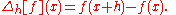
Depending on the application, the spacing h may be variable or constant.
A backward difference uses the function values at x and x − h, instead of the values at x + h and x:
Finally, the central difference is given by
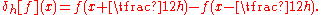
Relation with derivatives
The derivativeDerivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of a function f at a point x is defined by the limit
Limit of a function
In mathematics, the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input....
If h has a fixed (non-zero) value, instead of approaching zero, then the right-hand side is
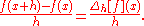
Hence, the forward difference divided by h approximates the derivative when h is small. The error in this approximation can be derived from Taylor's theorem
Taylor's theorem
In calculus, Taylor's theorem gives an approximation of a k times differentiable function around a given point by a k-th order Taylor-polynomial. For analytic functions the Taylor polynomials at a given point are finite order truncations of its Taylor's series, which completely determines the...
. Assuming that f is continuously differentiable, the error is
The same formula holds for the backward difference:
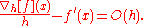
However, the central difference yields a more accurate approximation. Its error is proportional to square of the spacing (if f is twice continuously differentiable):
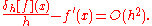
The main problem with the central difference method, however, is that oscillating functions can yield zero derivative. If f(nh)=1 for n uneven, and f(nh)=2 for n even, then f'(nh)=0 if it is calculated with the central difference scheme. This is particularly troublesome if the domain of f is discrete.
Higher-order differences
In an analogous way one can obtain finite difference approximations to higher order derivatives and differential operators. For example, by using the above central difference formula for
and 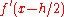and applying a central difference formula for the derivative of 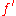at x, we obtain the central difference approximation of the second derivative of f:2nd Order Central
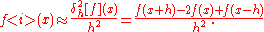
Similarly we can apply other differencing formulas in a recursive manner.
2nd Order Forward
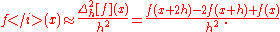
More generally, the nth-order forward, backward, and central differences are respectively given by:
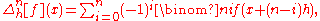
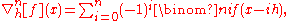
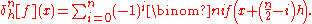
Note that the central difference will, for odd
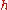, have multiplied by non-integers. This is often a problem because it amounts to changing the interval of discretization. The problem may be remedied taking the average of 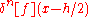and .The relationship of these higher-order differences with the respective derivatives is very straightforward:
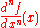
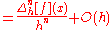
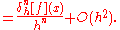
Higher-order differences can also be used to construct better approximations. As mentioned above, the first-order difference approximates the first-order derivative up to a term of order h. However, the combination
approximates f(x) up to a term of order h2. This can be proven by expanding the above expression in Taylor series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
, or by using the calculus of finite differences, explained below.
If necessary, the finite difference can be centered about any point by mixing forward, backward, and central differences.
Arbitrarily sized kernels
Using a little linear algebra, one can fairly easily construct approximations, which sample an arbitrary number of points to the left and a (possibly different) number of points to the right of the center point, for any order of derivative. This involves solving a linear system such that the Taylor expansion of the sum of those points, around the center point, well approximates the Taylor expansion of the desired derivative.This is useful for differentiating a function on a grid, where, as one approaches the edge of the grid, one must sample fewer and fewer points on one side.
The details are outlined in these notes.
Properties
- For all positive k and n
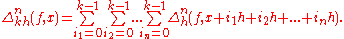
- Leibniz ruleLeibniz rule (generalized product rule)In calculus, the general Leibniz rule, named after Gottfried Leibniz, generalizes the product rule. It states that if f and g are n-times differentiable functions, then the nth derivative of the product fg is given by...
:
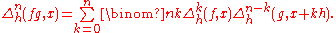
Finite difference methods
An important application of finite differences is in numerical analysisNumerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
, especially in numerical differential equations
Numerical partial differential equations
Numerical partial differential equations is the branch of numerical analysis that studies the numerical solution of partial differential equations .Numerical techniques for solving PDEs include the following:...
, which aim at the numerical solution of ordinary
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
and partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s respectively. The idea is to replace the derivatives appearing in the differential equation by finite differences that approximate them. The resulting methods are called finite difference method
Finite difference method
In mathematics, finite-difference methods are numerical methods for approximating the solutions to differential equations using finite difference equations to approximate derivatives.- Derivation from Taylor's polynomial :...
s.
Common applications of the finite difference method are in computational science and engineering disciplines, such as thermal engineering
Thermal engineering
Heating or cooling of processes, equipment, or enclosed environments are within the purview of thermal engineering.One or more of the following disciplines may be involved in solving a particular thermal engineering problem:*Thermodynamics*Fluid mechanics...
, fluid mechanics
Fluid mechanics
Fluid mechanics is the study of fluids and the forces on them. Fluid mechanics can be divided into fluid statics, the study of fluids at rest; fluid kinematics, the study of fluids in motion; and fluid dynamics, the study of the effect of forces on fluid motion...
, etc.
n-th difference
The nth forward difference of a function f(x) is given bywhere
is the binomial coefficientBinomial coefficient
In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
. Forward differences applied to a sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
are sometimes called the binomial transform of the sequence, and have a number of interesting combinatorial properties.
Forward differences may be evaluated using the Nörlund–Rice integral. The integral representation for these types of series is interesting because the integral can often be evaluated using asymptotic expansion
Asymptotic expansion
In mathematics an asymptotic expansion, asymptotic series or Poincaré expansion is a formal series of functions which has the property that truncating the series after a finite number of terms provides an approximation to a given function as the argument of the function tends towards a particular,...
or saddle-point techniques; by contrast, the forward difference series can be extremely hard to evaluate numerically, because the binomial coefficients grow rapidly for large n.
Newton's series
The Newton series consists of the terms of the Newton forward difference equation, named after Isaac NewtonIsaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
; in essence, it is the Newton interpolation formula, first published in his Principia Mathematica in 1687, namely the discrete analog of the continuum Taylor expansion,
-
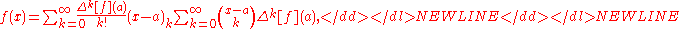
which holds for any polynomialPolynomialIn mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
function f and for most (but not all) analytic functionAnalytic functionIn mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
s. Here, the expression
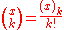
is the binomial coefficientBinomial coefficientIn mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
, and
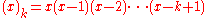
is the "falling factorial" or "lower factorial", while the empty productEmpty productIn mathematics, an empty product, or nullary product, is the result of multiplying no factors. It is equal to the multiplicative identity 1, given that it exists for the multiplication operation in question, just as the empty sum—the result of adding no numbers—is zero, or the additive...
(x)0 is defined to be 1. In this particular case, there is an assumption of unit steps for the changes in the values of x, h=1 of the generalization below.
Note also the formal correspondence of this result to Taylor's theoremTaylor's theoremIn calculus, Taylor's theorem gives an approximation of a k times differentiable function around a given point by a k-th order Taylor-polynomial. For analytic functions the Taylor polynomials at a given point are finite order truncations of its Taylor's series, which completely determines the...
; historically, this, as well as the Chu-Vandermonde identity,
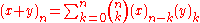, following from it, is one of the observations that matured to the system of the umbral calculusUmbral calculusIn mathematics before the 1970s, the term umbral calculus referred to the surprising similarity between seemingly unrelated polynomial equations and certain shadowy techniques used to 'prove' them. These techniques were introduced by and are sometimes called Blissard's symbolic method...
.
To illustrate how one might use Newton's formula in actual practice, consider the first few terms of the Fibonacci sequence f = 2, 2, 4... One can thus find a polynomialPolynomialIn mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
that reproduces these values, by first computing a difference table, and then substituting the differences which correspond to x0 (underlined) into the formula as follows,
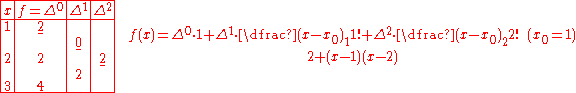
For the case of nonuniform steps in the values of x, Newton computes the divided differencesDivided differencesIn mathematics divided differences is a recursive division process.The method can be used to calculate the coefficients in the interpolation polynomial in the Newton form.-Definition:Given n data points,\ldots,...
,
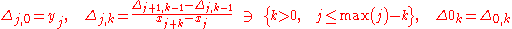
the series of products,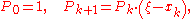
and the resulting polynomial is the scalar product,
.
In analysis with p-adic numberP-adic numberIn mathematics, and chiefly number theory, the p-adic number system for any prime number p extends the ordinary arithmetic of the rational numbers in a way different from the extension of the rational number system to the real and complex number systems...
s, Mahler's theoremMahler's theoremIn mathematics, Mahler's theorem, introduced by , expresses continuous p-adic functions in terms of polynomials.In any field, one has the following result. Let=f-f\,be the forward difference operator...
states that the assumption that f is a polynomial function can be weakened all the way to the assumption that f is merely continuous.
Carlson's theoremCarlson's theoremIn mathematics, in the area of complex analysis, Carlson's theorem is a uniqueness theorem about a summable expansion of an analytic function. It is typically invoked to defend the uniqueness of a Newton series expansion. Carlson's theorem has generalized analogues for expansions in other bases of...
provides necessary and sufficient conditions for a Newton series to be unique, if it exists. However, a Newton series will not, in general, exist.
The Newton series, together with the Stirling series and the Selberg series, is a special case of the general difference series, all of which are defined in terms of scaled forward differences.
In a compressed and slightly more general form and equidistant nodes the formula reads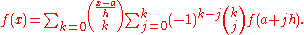
Calculus of finite differences
The forward difference can be considered as a difference operator, which maps the function f to Δh[f]. This operator amounts to
where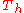
is the shift operatorShift operatorIn mathematics, and in particular functional analysis, the shift operator or translation operator is an operator that takes a function to its translation . In time series analysis, the shift operator is called the lag operator....
with step
, defined by 
, and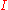 
is an identity operator.
The finite difference of higher orders can be defined in recursive manner as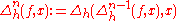
or, in operator notation,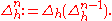
Another equivalent definition is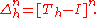
The difference operator Δh is a linear and satisfies a Leibniz ruleLeibniz rule (generalized product rule)In calculus, the general Leibniz rule, named after Gottfried Leibniz, generalizes the product rule. It states that if f and g are n-times differentiable functions, then the nth derivative of the product fg is given by...
. Similar statements hold for the backward and central differences.
Formally applying the Taylor seriesTaylor seriesIn mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
with respect to h yields the formula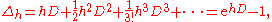
where D denotes the continuum derivative operator, mapping f to its derivative f. The expansion is valid when both sides act on analytic functionAnalytic functionIn mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
s, for sufficiently small h. Formally inverting the exponential suggests that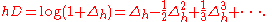
This formula holds in the sense that both operators give the same result when applied to a polynomial. Even for analytic functions, the series on the right is not guaranteed to converge; it may be an asymptotic series. However, it can be used to obtain more accurate approximations for the derivative. For instance, retaining the first two terms of the series yields the second-order approximation to f’(x) mentioned at the end of the section Higher-order differences.
The analogous formulas for the backward and central difference operators are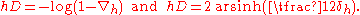
The calculus of finite differences is related to the umbral calculusUmbral calculusIn mathematics before the 1970s, the term umbral calculus referred to the surprising similarity between seemingly unrelated polynomial equations and certain shadowy techniques used to 'prove' them. These techniques were introduced by and are sometimes called Blissard's symbolic method...
of combinatorics. This remarkably systematic correspondence is due to the identity of the commutators of the umbral quantities to their continuum analogs (h→0 limits),
A large number of formal differential relations of standard calculus involving
functions f(x) thus map systematically to umbral finite-difference analogs involving f(xTh−1).
For instance, the umbral analog of a monomial xn is a generalization of the above falling factorial (Pochhammer k-symbolPochhammer k-symbolIn the mathematical theory of special functions, the Pochhammer k-symbol and the k-gamma function, introduced by Rafael Díaz and Eddy Pariguan, are generalizations of the Pochhammer symbol and gamma function...
),
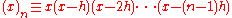, so that
hence the above Newton interpolation formula (by matching coefficients in the expansion of an arbitrary function f(x) in such symbols), and so on.
As in the continuum limit, the eigenfunction of
also happens to be an exponential,
and hence Fourier sums of continuum functions are readily mapped to umbral Fourier sums faithfully, i.e., involving the same Fourier coefficients multiplying these umbral basis exponentials.
Thus, for instance, the Dirac delta functionDirac delta functionThe Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
maps to its umbral correspondent, the cardinal sine function,
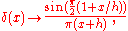
and so forth. Difference equations can often be solved with techniques very similar to those for solving differential equationDifferential equationA differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
s.
The inverse operator of the forward difference operator, the umbral integral, is the indefinite sum or antidifference operator.
Rules for calculus of finite difference operators
Analogous to rules for finding the derivative, we have:- Constant rule: If c is a constantConstant (mathematics)In mathematics, a constant is a non-varying value, i.e. completely fixed or fixed in the context of use. The term usually occurs in opposition to variable In mathematics, a constant is a non-varying value, i.e. completely fixed or fixed in the context of use. The term usually occurs in opposition...
, then
- LinearityLinearity of differentiationIn mathematics, the linearity of differentiation is a most fundamental property of the derivative, in differential calculus. It follows from the sum rule in differentiation and the constant factor rule in differentiation...
: if a and b are constantsConstant (mathematics)In mathematics, a constant is a non-varying value, i.e. completely fixed or fixed in the context of use. The term usually occurs in opposition to variable In mathematics, a constant is a non-varying value, i.e. completely fixed or fixed in the context of use. The term usually occurs in opposition...
,
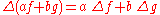
All of the above rules apply equally well to any difference operator, including
as to 
.
- Product ruleProduct ruleIn calculus, the product rule is a formula used to find the derivatives of products of two or more functions. It may be stated thus:'=f'\cdot g+f\cdot g' \,\! or in the Leibniz notation thus:...
:
- Quotient rule:
-
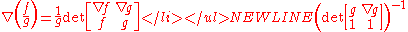
- or
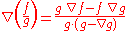
- or
- Summation rules:
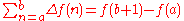
Generalizations
- A generalized finite difference is usually defined as
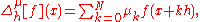
where
is its coefficients vector. An infinite difference is a further generalization, where the finite sum above is replaced by an infinite seriesSeries (mathematics)A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
. Another way of generalization is making coefficients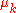
depend on point 
: 
, thus considering weighted finite difference. Also one may make step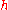 
depend on point 
: 
. Such generalizations are useful for constructing different modulus of continuityModulus of continuityIn mathematical analysis, a modulus of continuity is a function\omega:[0,\infty]\to[0,\infty]used to measure quantitatively the uniform continuity of functions. So, a function f:I\to\R admits \omega as a modulus of continuity if and only if|f-f|\leq\omega,for all x and y in the domain of f...
.
- Difference operator generalizes to Möbius inversion over a partially ordered setPartially ordered setIn mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
.
- As a convolution operator: Via the formalism of incidence algebraIncidence algebraIn order theory, a field of mathematics, an incidence algebra is an associative algebra, defined for any locally finite partially ordered setand commutative ring with unity.-Definition:...
s, difference operators and other Möbius inversion can be represented by convolutionConvolutionIn mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
with a function on the poset, called the Möbius functionMöbius functionThe classical Möbius function μ is an important multiplicative function in number theory and combinatorics. The German mathematician August Ferdinand Möbius introduced it in 1832...
μ; for the difference operator, μ is the sequence (1, −1, 0, 0, 0, ...).
Finite difference in several variables
Finite differences can be considered in more than one variable. They are analogous to partial derivativePartial derivativeIn mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
s in several variables.
Some partial derivative approximations are:
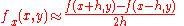
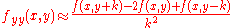
See also
- Finite difference coefficients
- Newton polynomialNewton polynomialIn the mathematical field of numerical analysis, a Newton polynomial, named after its inventor Isaac Newton, is the interpolation polynomial for a given set of data points in the Newton form...
- Table of Newtonian series
- Sheffer sequence
- Umbral calculusUmbral calculusIn mathematics before the 1970s, the term umbral calculus referred to the surprising similarity between seemingly unrelated polynomial equations and certain shadowy techniques used to 'prove' them. These techniques were introduced by and are sometimes called Blissard's symbolic method...
- Taylor seriesTaylor seriesIn mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
- Numerical differentiationNumerical differentiationIn numerical analysis, numerical differentiation describes algorithms for estimating the derivative of a mathematical function or function subroutine using values of the function and perhaps other knowledge about the function.-Finite difference formulae:...
- Five-point stencilFive-point stencilIn numerical analysis, given a square grid in one or two dimensions, the five-point stencil of a point in the grid is made up of the point itself together with its four "neighbors"...
- Divided differencesDivided differencesIn mathematics divided differences is a recursive division process.The method can be used to calculate the coefficients in the interpolation polynomial in the Newton form.-Definition:Given n data points,\ldots,...
- Modulus of continuityModulus of continuityIn mathematical analysis, a modulus of continuity is a function\omega:[0,\infty]\to[0,\infty]used to measure quantitatively the uniform continuity of functions. So, a function f:I\to\R admits \omega as a modulus of continuity if and only if|f-f|\leq\omega,for all x and y in the domain of f...
- Time scale calculusTime scale calculusIn mathematics, time-scale calculus is a unification of the theory of difference equations with that of differential equations, unifying integral and differential calculus with the calculus of finite differences, offering a formalism for studying hybrid discrete–continuous dynamical systems...
- Summation by parts
- Lagrange polynomialLagrange polynomialIn numerical analysis, Lagrange polynomials are used for polynomial interpolation. For a given set of distinct points x_j and numbers y_j, the Lagrange polynomial is the polynomial of the least degree that at each point x_j assumes the corresponding value y_j...
- Gilbreath's conjectureGilbreath's conjectureGilbreath's conjecture is a hypothesis, or a conjecture, in number theory regarding the sequences generated by applying the forward difference operator to consecutive prime numbers and leaving the results unsigned, and then repeating this process on consecutive terms in the resulting sequence, and...
External links
- http://reference.wolfram.com/mathematica/tutorial/NDSolvePDE.html#c:4Table of useful finite difference formula generated using MathematicaMathematicaMathematica is a computational software program used in scientific, engineering, and mathematical fields and other areas of technical computing...
] - Finite Calculus: A Tutorial for Solving Nasty Sums
- Central Differences: Simple derivation, Reference formulas, Frequency domain properties. Possible alternative approaches
-
-
