Lipschitz continuity
Encyclopedia
In mathematical analysis
, Lipschitz continuity, named after Rudolf Lipschitz
, is a strong form of uniform continuity
for function
s. Intuitively, a Lipschitz continuous function
is limited in how fast it can change: for every pair of points on the graph of this function, the absolute value of the slope of the line connecting them is no greater than a definite real number; this bound is called the function's "Lipschitz constant" (or "modulus of uniform continuity
").
In the theory of differential equation
s, Lipschitz continuity is the central condition of the Picard–Lindelöf theorem
which guarantees the existence and uniqueness of the solution to an initial value problem
. A special type of Lipschitz continuity, called contraction
, is used in the Banach fixed point theorem
.
The concept of Lipschitz continuity is well-defined on metric space
s. A generalisation of Lipschitz continuity is called Hölder continuity.
Given two metric space
s (X, dX) and (Y, dY), where dX denotes the metric
on the set X and dY is the metric on set Y (for example, Y might be the set of real number
s R with the metric dY(x, y) = |x − y|, and X might be a subset of R), a function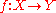
is called Lipschitz continuous if there exists a real constant K ≥ 0 such that, for all x1 and x2 in X,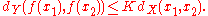
Any such K is referred to as a Lipschitz constant for the function ƒ. The smallest constant is sometimes called the (best) Lipschitz constant; however in most cases the latter notion is less relevant. If K = 1 the function is called a short map
, and if 0 ≤ K < 1 the function is called a contraction
.
The inequality is (trivially) satisfied if x1 = x2. Otherwise, one can equivalently define a function to be Lipschitz continuous if and only if
there exists a constant K ≥ 0 such that, for all x1 ≠ x2,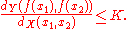
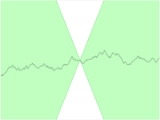
For real-valued functions of several real variables, this holds if and only if the slopes of all secant lines are bounded by K. The set of lines of slope K passing through a point on the graph of the function forms a circular cone, and a function is Lipschitz if and only if the graph of the function everywhere lies completely outside of this cone (see figure).
A function is called locally Lipschitz continuous if for every x in X there exists a neighborhood U of x such that f restricted to U is Lipschitz continuous. Equivalently, if X is a locally compact metric space, then ƒ is locally Lipschitz if and only if it is Lipschitz continuous on every compact subset of X. In spaces that are not locally compact, this is a necessary but not a sufficient condition.
More generally, a function f defined on X is said to be Hölder continuous or to satisfy a Hölder condition
of order α > 0 on X if there exists a constant M > 0 such that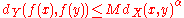
for all x and y in X. Sometimes a Hölder condition of order α is also called a uniform Lipschitz condition of order α > 0.
If there exists a K ≥ 1 with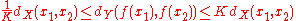
then ƒ is called bilipschitz (also written bi-Lipschitz). A bilipschitz mapping is injective
, and is in fact a homeomorphism
onto its image. A bilipschitz function is the same thing as an injective Lipschitz function whose inverse function
is also Lipschitz. Surjective bilipschitz functions are exactly the isomorphisms of metric spaces.
Continuous functions that are not (globally) Lipschitz continuous:
Differentiable functions that are not (globally) Lipschitz continuous:
Using bi-Lipschitz mappings, it is possible to define a Lipschitz structure on a topological manifold
, since there is a pseudogroup
structure on bi-Lipschitz homeomorphisms. This structure is intermediate between that of a piecewise-linear manifold and a smooth manifold. In fact a PL structure gives rise to a unique Lipschitz structure; it can in that sense 'nearly' be smoothed.
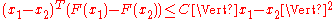
for some C for all x1 and x2.
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, Lipschitz continuity, named after Rudolf Lipschitz
Rudolf Lipschitz
Rudolf Otto Sigismund Lipschitz was a German mathematician and professor at the University of Bonn from 1864. Peter Gustav Dirichlet was his teacher. He supervised the early work of Felix Klein....
, is a strong form of uniform continuity
Uniform continuity
In mathematics, a function f is uniformly continuous if, roughly speaking, it is possible to guarantee that f and f be as close to each other as we please by requiring only that x and y are sufficiently close to each other; unlike ordinary continuity, the maximum distance between x and y cannot...
for function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s. Intuitively, a Lipschitz continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
is limited in how fast it can change: for every pair of points on the graph of this function, the absolute value of the slope of the line connecting them is no greater than a definite real number; this bound is called the function's "Lipschitz constant" (or "modulus of uniform continuity
Modulus of continuity
In mathematical analysis, a modulus of continuity is a function\omega:[0,\infty]\to[0,\infty]used to measure quantitatively the uniform continuity of functions. So, a function f:I\to\R admits \omega as a modulus of continuity if and only if|f-f|\leq\omega,for all x and y in the domain of f...
").
In the theory of differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
s, Lipschitz continuity is the central condition of the Picard–Lindelöf theorem
Picard–Lindelöf theorem
In mathematics, in the study of differential equations, the Picard–Lindelöf theorem, Picard's existence theorem or Cauchy–Lipschitz theorem is an important theorem on existence and uniqueness of solutions to first-order equations with given initial conditions.The theorem is named after Charles...
which guarantees the existence and uniqueness of the solution to an initial value problem
Initial value problem
In mathematics, in the field of differential equations, an initial value problem is an ordinary differential equation together with a specified value, called the initial condition, of the unknown function at a given point in the domain of the solution...
. A special type of Lipschitz continuity, called contraction
Contraction mapping
In mathematics, a contraction mapping, or contraction, on a metric space is a function f from M to itself, with the property that there is some nonnegative real number k...
, is used in the Banach fixed point theorem
Banach fixed point theorem
In mathematics, the Banach fixed-point theorem is an important tool in the theory of metric spaces; it guarantees the existence and uniqueness of fixed points of certain self-maps of metric spaces, and provides a constructive method to find those fixed points...
.
The concept of Lipschitz continuity is well-defined on metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
s. A generalisation of Lipschitz continuity is called Hölder continuity.
Definitions
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
s (X, dX) and (Y, dY), where dX denotes the metric
Metric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
on the set X and dY is the metric on set Y (for example, Y might be the set of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s R with the metric dY(x, y) = |x − y|, and X might be a subset of R), a function
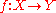
is called Lipschitz continuous if there exists a real constant K ≥ 0 such that, for all x1 and x2 in X,
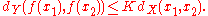
Any such K is referred to as a Lipschitz constant for the function ƒ. The smallest constant is sometimes called the (best) Lipschitz constant; however in most cases the latter notion is less relevant. If K = 1 the function is called a short map
Short map
In the mathematical theory of metric spaces, a metric map is a function between metric spaces that does not increase any distance .These maps are the morphisms in the category of metric spaces, Met ....
, and if 0 ≤ K < 1 the function is called a contraction
Contraction mapping
In mathematics, a contraction mapping, or contraction, on a metric space is a function f from M to itself, with the property that there is some nonnegative real number k...
.
The inequality is (trivially) satisfied if x1 = x2. Otherwise, one can equivalently define a function to be Lipschitz continuous if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
there exists a constant K ≥ 0 such that, for all x1 ≠ x2,
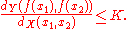
For real-valued functions of several real variables, this holds if and only if the slopes of all secant lines are bounded by K. The set of lines of slope K passing through a point on the graph of the function forms a circular cone, and a function is Lipschitz if and only if the graph of the function everywhere lies completely outside of this cone (see figure).
A function is called locally Lipschitz continuous if for every x in X there exists a neighborhood U of x such that f restricted to U is Lipschitz continuous. Equivalently, if X is a locally compact metric space, then ƒ is locally Lipschitz if and only if it is Lipschitz continuous on every compact subset of X. In spaces that are not locally compact, this is a necessary but not a sufficient condition.
More generally, a function f defined on X is said to be Hölder continuous or to satisfy a Hölder condition
Hölder condition
In mathematics, a real or complex-valued function ƒ on d-dimensional Euclidean space satisfies a Hölder condition, or is Hölder continuous, when there are nonnegative real constants C, \alpha , such that...
of order α > 0 on X if there exists a constant M > 0 such that
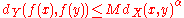
for all x and y in X. Sometimes a Hölder condition of order α is also called a uniform Lipschitz condition of order α > 0.
If there exists a K ≥ 1 with
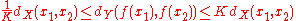
then ƒ is called bilipschitz (also written bi-Lipschitz). A bilipschitz mapping is injective
Injective function
In mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
, and is in fact a homeomorphism
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
onto its image. A bilipschitz function is the same thing as an injective Lipschitz function whose inverse function
Inverse function
In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
is also Lipschitz. Surjective bilipschitz functions are exactly the isomorphisms of metric spaces.
Examples
Lipschitz continuous functions- The function f(x) = defined for all real numbers is Lipschitz continuous with the Lipschitz constant K = 1, because it is everywhere differentiable and the absolute value of the derivative is bounded above by 1.
- Likewise, the sineSineIn mathematics, the sine function is a function of an angle. In a right triangle, sine gives the ratio of the length of the side opposite to an angle to the length of the hypotenuse.Sine is usually listed first amongst the trigonometric functions....
function is Lipschitz continuous because its derivative, the cosine function, is bounded above by 1 in absolute value.
- The function f(x) = |x| defined on the reals is Lipschitz continuous with the Lipschitz constant equal to 1, by the reverse triangle inequality. This is an example of a Lipschitz continuous function that is not differentiable. More generally, a normNorm (mathematics)In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
on a vector space is Lipschitz continuous with respect to the associated metric, with the Lipschitz constant equal to 1.
Continuous functions that are not (globally) Lipschitz continuous:
- The function f(x) = x2 with domain all real numbers is not Lipschitz continuous. This function becomes arbitrarily steep as x approaches infinity. It is however locally Lipschitz continuous.
- The function f(x) = defined on [0, 1] is not Lipschitz continuous. This function becomes infinitely steep as x approaches 0 since its derivative becomes infinite. However, it is uniformly continuous as well as Hölder continuous of class C0, α for α ≤ 1/2.
Differentiable functions that are not (globally) Lipschitz continuous:
- The function f(x) = x3/2sin(1/x) (x ≠ 0) and f(0) = 0, restricted on [0, 1], gives an example of a function that is differentiable on a compact set while not locally Lipschitz because its derivative function is not bounded. See also the first property below.
Properties
- An everywhere differentiable function g : R → R is Lipschitz continuous (with K = sup |g′(x)|) if and only if it has bounded first derivative; one direction follows from the mean value theoremMean value theoremIn calculus, the mean value theorem states, roughly, that given an arc of a differentiable curve, there is at least one point on that arc at which the derivative of the curve is equal to the "average" derivative of the arc. Briefly, a suitable infinitesimal element of the arc is parallel to the...
. In particular, any C1 function is locally Lipschitz, as continuous functions on a locally compact space are locally bounded so its gradient is.
- A Lipschitz function g : R → R is absolutely continuous and therefore is differentiable almost everywhereAlmost everywhereIn measure theory , a property holds almost everywhere if the set of elements for which the property does not hold is a null set, that is, a set of measure zero . In cases where the measure is not complete, it is sufficient that the set is contained within a set of measure zero...
, that is, differentiable at every point outside a set of Lebesgue measureLebesgue measureIn measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
zero. Its derivative is essentially bounded in magnitude by the Lipschitz constant, and for a < b, the difference g(b) − g(a) is equal to the integral of the derivative g′ on the interval [a, b].- Conversely, if ƒ : I → R is absolutely continuous and thus differentiable almost everywhere, and satisfies |ƒ′(x)| ≤ K for almost all x in I, then ƒ is Lipschitz continuous with Lipschitz constant at most K.
- More generally, Rademacher's theoremRademacher's theoremIn mathematical analysis, Rademacher's theorem, named after Hans Rademacher, states the following: If U is an open subset of Rn andis Lipschitz continuous, then f is Fréchet-differentiable almost everywhere in U In mathematical analysis, Rademacher's theorem, named after Hans Rademacher, states the...
extends the differentiability result to Lipschitz mappings between Euclidean spaces: a Lipschitz map ƒ : U → Rm, where U is an open set in Rn, is almost everywhereAlmost everywhereIn measure theory , a property holds almost everywhere if the set of elements for which the property does not hold is a null set, that is, a set of measure zero . In cases where the measure is not complete, it is sufficient that the set is contained within a set of measure zero...
differentiableDerivativeIn calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
. Moreover, if K is the best Lipschitz constant of ƒ, then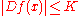
whenever the total derivativeTotal derivativeIn the mathematical field of differential calculus, the term total derivative has a number of closely related meanings.The total derivative of a function f, of several variables, e.g., t, x, y, etc., with respect to one of its input variables, e.g., t, is different from the partial derivative...
Dƒ exists .
- For a differentiable Lipschitz map ƒ : U → Rm the inequality
holds for the best Lipschitz constant of f, and it turns out to be an equality if the domain U is convex. - Suppose that
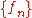is a sequence of Lipschitz continuous mappings between two metric spaces, and that all 
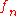have Lipschitz constant bounded by some K. If ƒn converges to a mapping ƒ uniformly, then ƒ is also Lipschitz, with Lipschitz constant bounded by the same K. In particular, this implies that the set of real-valued functions on a compact metric space with a particular bound for the Lipschitz constant is a closed and convex subset of the Banach spaceBanach spaceIn mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
of continuous functions. This result does not hold for sequences in which the functions may have unbounded Lipschitz constants, however. In fact, the space of all Lipschitz functions on a compact metric space is dense in the Banach space of continuous functions, an elementary consequence of the Stone–Weierstrass theorem. - Every Lipschitz continuous map is uniformly continuous, and hence a fortiori continuousContinuous functionIn mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
. More generally, a set of functions with bounded Lipschitz constant forms an equicontinuous set. The Arzelà–Ascoli theorem implies that if
is a uniformly bounded sequence of functions with bounded Lipschitz constant, then it has a convergent subsequence. By the result of the previous paragraph, the limit function is also Lipschitz, with the same bound for the Lipschitz constant. In particular the set of all real-valued Lipschitz functions on a compact metric space X having Lipschitz constant ≤ K is a locally compactLocally compact spaceIn topology and related branches of mathematics, a topological space is called locally compact if, roughly speaking, each small portion of the space looks like a small portion of a compact space.-Formal definition:...
convex subset of the Banach space C(X). - If U is a subset of the metric space M and ƒ : U → R is a Lipschitz continuous function, there always exist Lipschitz continuous maps M → R which extend ƒ and have the same Lipschitz constant as ƒ (see also Kirszbraun theoremKirszbraun theoremIn mathematics, specifically real analysis and functional analysis, the Kirszbraun theorem states that if U is a subset of some Hilbert space H1, and H2 is another Hilbert space, and...
). An extension is provided by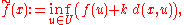
where k is a Lipschitz constant for ƒ on U.
Lipschitz manifolds
Let U and V be two open sets in Rn. A function T : U → V is called bi-Lipschitz if it is a Lipschitz homeomorphism onto its image, and its inverse is also Lipschitz.Using bi-Lipschitz mappings, it is possible to define a Lipschitz structure on a topological manifold
Topological manifold
In mathematics, a topological manifold is a topological space which looks locally like Euclidean space in a sense defined below...
, since there is a pseudogroup
Pseudogroup
In mathematics, a pseudogroup is an extension of the group concept, but one that grew out of the geometric approach of Sophus Lie, rather than out of abstract algebra...
structure on bi-Lipschitz homeomorphisms. This structure is intermediate between that of a piecewise-linear manifold and a smooth manifold. In fact a PL structure gives rise to a unique Lipschitz structure; it can in that sense 'nearly' be smoothed.
One-sided Lipschitz
Let F(x) be an upper semi-continuous function of x, and that F(x) is a closed, convex set for all x. Then F is one-sided Lipschitz if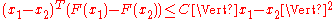for some C for all x1 and x2.