Utility
Encyclopedia
In economics
, utility is a measure of customer satisfaction, referring to the total satisfaction received by a consumer from consuming a good or service.
Given this measure, one may speak meaningfully of increasing or decreasing utility, and thereby explain economic behavior in terms of attempts to increase one's utility. Utility is often modeled to be affected by consumption
of various goods and services
, possession of wealth and spending of leisure time.
The doctrine of utilitarianism
saw the maximization of utility as a moral criterion for the organization of society. According to utilitarians, such as Jeremy Bentham
(1748–1832) and John Stuart Mill
(1806–1873), society should aim to maximize the total utility of individuals, aiming for "the greatest happiness
for the greatest number of people". Another theory forwarded by John Rawls
(1921–2002) would have society maximize the utility of those with the lowest utility, raising them up to create a more equitable distribution across society.
Utility is usually applied by economists in such constructs as the indifference curve
, which plot the combination of commodities that an individual or a society would accept to maintain a given level of satisfaction. Individual utility and social utility can be construed as the value of a utility function and a social welfare function
respectively. When coupled with production or commodity constraints, under some assumptions, these functions can be used to analyze Pareto efficiency
, such as illustrated by Edgeworth box
es in contract curve
s. Such efficiency is a central concept in welfare economics
.
In finance
, utility is applied to generate an individual's price for an asset
called the indifference price
. Utility functions are also related to risk measure
s, with the most common example being the entropic risk measure
.
, were revealed in price:
and ordinal utility
. When cardinal utility is used, the magnitude of utility differences is treated as an ethically or behaviorally significant quantity. On the other hand, ordinal utility captures only ranking and not strength of preferences.
Utility functions of both sorts assign a ranking to members of a choice set. For example, suppose a cup of orange juice has utility of 120 utils, a cup of tea has a utility of 80 utils, and a cup of water has a utility of 40 utils. When speaking of cardinal utility, it could be concluded that the cup of orange juice is better than the cup of tea by exactly the same amount by which the cup of tea is better than the cup of water. One is not entitled to conclude, however, that the cup of tea is two thirds as good as the cup of juice, because this conclusion would depend not only on magnitudes of utility differences, but also on the "zero" of utility.
It is tempting when dealing with cardinal utility to aggregate utilities across persons. The argument against this is that interpersonal comparisons of utility are meaningless because there is no good way to interpret how different people value consumption bundles.
When ordinal utilities are used, differences in utils are treated as ethically or behaviorally meaningless: the utility index encode a full behavioral ordering between members of a choice set, but tells nothing about the related strength of preferences. In the above example, it would only be possible to say that juice is preferred to tea to water, but no more.
Neoclassical economics
has largely retreated from using cardinal utility functions as the basic objects of economic analysis, in favor of considering agent preference
s over choice sets. However, preference relations can often be represented by utility functions satisfying several properties.
Ordinal utility functions are unique up to
positive monotone transformations, while cardinal utilities are unique up to positive linear transformations.
Although preference
s are the conventional foundation of microeconomics
, it is often convenient to represent preferences with a utility function
and analyze human behavior indirectly with utility functions. Let X be the consumption set, the set of all mutually-exclusive baskets the consumer could conceivably consume. The consumer's utility function
ranks each package in the consumption set. If the consumer strictly prefers x to y or is indifferent between them, then u(x) > u(y).
For example, suppose a consumer's consumption set is X = {nothing, 1 apple,1 orange, 1 apple and 1 orange, 2 apples, 2 oranges}, and its utility function is u(nothing) = 0, u(1 apple) = 1, u(1 orange) = 2, u(1 apple and 1 orange) = 4, u(2 apples) = 2 and u(2 oranges) = 3. Then this consumer prefers 1 orange to 1 apple, but prefers one of each to 2 oranges.
In microeconomic models, there are usually a finite set of L commodities, and a consumer may consume an arbitrary amount of each commodity. This gives a consumption set of
, and each package 
is a vector containing the amounts of each commodity. In the previous example, we might say there are two commodities: apples and oranges. If we say apples is the first commodity, and oranges the second, then the consumption set 
and u(0, 0) = 0, u(1, 0) = 1, u(0, 1) = 2, u(1, 1) = 4, u(2, 0) = 2, u(0, 2) = 3 as before. Note that for u to be a utility function on X, it must be defined for every package in X.
A utility function
represents a preference relation 
on X iff
for every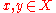
, 
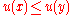implies 
. If u represents 
, then this implies 
is complete and transitive, and hence rational.
In order to simplify calculations, various assumptions have been made of utility functions.
Most utility functions used in modeling or theory are well-behaved. They are usually monotonic, quasi-concave, continuous and globally non-satiated. However, it is possible for preferences not to be representable by a utility function. An example is lexicographic preferences
which are not continuous and cannot be represented by a continuous utility function.
The expected utility model was first proposed by Nicholas Bernoulli in 1713 and solved by Daniel Bernoulli
in 1738 as the St. Petersburg paradox
. Bernoulli argued that the paradox could be resolved if decisionmakers displayed risk aversion
and argued for a logarithmic cardinal utility function.
The first important use of the expected utility theory was that of John von Neumann
and Oskar Morgenstern
who used the assumption of expected utility maximization in their formulation of game theory
.
The reason is that the utility of twenty sandwiches is not twenty times the utility of one sandwich, by the law of diminishing returns. So it is hard to compare the utility of the shirt with 'twenty times the utility of the sandwich'. But Von Neumann and Morgenstern suggested an unambiguous way of making a comparison like this.
Their method of comparison involves considering probabilities. If a person can choose between various randomized events (lotteries), then it is possible to additively compare the shirt and the sandwich. It is possible to compare a sandwich with probability 1, to a shirt with probability p or nothing with probability 1 − p. By adjusting p, the point at which the sandwich becomes preferable defines the ratio of the utilities of the two options.
A notation for a lottery is as follows: if options A and B have probability p and 1 − p in the lottery, write it as a linear combination:
Economics
Economics is the social science that analyzes the production, distribution, and consumption of goods and services. The term economics comes from the Ancient Greek from + , hence "rules of the house"...
, utility is a measure of customer satisfaction, referring to the total satisfaction received by a consumer from consuming a good or service.
Given this measure, one may speak meaningfully of increasing or decreasing utility, and thereby explain economic behavior in terms of attempts to increase one's utility. Utility is often modeled to be affected by consumption
Consumption (economics)
Consumption is a common concept in economics, and gives rise to derived concepts such as consumer debt. Generally, consumption is defined in part by comparison to production. But the precise definition can vary because different schools of economists define production quite differently...
of various goods and services
Goods and services
In economics, economic output is divided into physical goods and intangible services. Consumption of goods and services is assumed to produce utility. It is often used when referring to a Goods and Services Tax....
, possession of wealth and spending of leisure time.
The doctrine of utilitarianism
Utilitarianism
Utilitarianism is an ethical theory holding that the proper course of action is the one that maximizes the overall "happiness", by whatever means necessary. It is thus a form of consequentialism, meaning that the moral worth of an action is determined only by its resulting outcome, and that one can...
saw the maximization of utility as a moral criterion for the organization of society. According to utilitarians, such as Jeremy Bentham
Jeremy Bentham
Jeremy Bentham was an English jurist, philosopher, and legal and social reformer. He became a leading theorist in Anglo-American philosophy of law, and a political radical whose ideas influenced the development of welfarism...
(1748–1832) and John Stuart Mill
John Stuart Mill
John Stuart Mill was a British philosopher, economist and civil servant. An influential contributor to social theory, political theory, and political economy, his conception of liberty justified the freedom of the individual in opposition to unlimited state control. He was a proponent of...
(1806–1873), society should aim to maximize the total utility of individuals, aiming for "the greatest happiness
Happiness
Happiness is a mental state of well-being characterized by positive emotions ranging from contentment to intense joy. A variety of biological, psychological, religious, and philosophical approaches have striven to define happiness and identify its sources....
for the greatest number of people". Another theory forwarded by John Rawls
John Rawls
John Bordley Rawls was an American philosopher and a leading figure in moral and political philosophy. He held the James Bryant Conant University Professorship at Harvard University....
(1921–2002) would have society maximize the utility of those with the lowest utility, raising them up to create a more equitable distribution across society.
Utility is usually applied by economists in such constructs as the indifference curve
Indifference curve
In microeconomic theory, an indifference curve is a graph showing different bundles of goods between which a consumer is indifferent. That is, at each point on the curve, the consumer has no preference for one bundle over another. One can equivalently refer to each point on the indifference curve...
, which plot the combination of commodities that an individual or a society would accept to maintain a given level of satisfaction. Individual utility and social utility can be construed as the value of a utility function and a social welfare function
Social welfare function
In economics, a social welfare function is a real-valued function that ranks conceivable social states from lowest to highest. Inputs of the function include any variables considered to affect the economic welfare of a society...
respectively. When coupled with production or commodity constraints, under some assumptions, these functions can be used to analyze Pareto efficiency
Pareto efficiency
Pareto efficiency, or Pareto optimality, is a concept in economics with applications in engineering and social sciences. The term is named after Vilfredo Pareto, an Italian economist who used the concept in his studies of economic efficiency and income distribution.Given an initial allocation of...
, such as illustrated by Edgeworth box
Edgeworth box
In economics, an Edgeworth box, named after Francis Ysidro Edgeworth, is a way of representing various distributions of resources. Edgeworth made his presentation in his book Mathematical Psychics: An Essay on the Application of Mathematics to the Moral Sciences, 1881...
es in contract curve
Contract curve
In microeconomics, the contract curve is the set of points, representing final allocations of two goods between two people, that could occur as a result of voluntary trading between those people given their initial allocations of the goods...
s. Such efficiency is a central concept in welfare economics
Welfare economics
Welfare economics is a branch of economics that uses microeconomic techniques to evaluate economic well-being, especially relative to competitive general equilibrium within an economy as to economic efficiency and the resulting income distribution associated with it...
.
In finance
Finance
"Finance" is often defined simply as the management of money or “funds” management Modern finance, however, is a family of business activity that includes the origination, marketing, and management of cash and money surrogates through a variety of capital accounts, instruments, and markets created...
, utility is applied to generate an individual's price for an asset
Asset
In financial accounting, assets are economic resources. Anything tangible or intangible that is capable of being owned or controlled to produce value and that is held to have positive economic value is considered an asset...
called the indifference price
Indifference price
In finance, indifference pricing is a method of pricing financial securities with regards to a utility function. Also known as the reservation price or private valuation. Particularly the indifference price is the price that an agent would have the same expected utility level between exercising a...
. Utility functions are also related to risk measure
Risk measure
A Risk measure is used to determine the amount of an asset or set of assets to be kept in reserve. The purpose of this reserve is to make the risks taken by financial institutions, such as banks and insurance companies, acceptable to the regulator...
s, with the most common example being the entropic risk measure
Entropic risk measure
In financial mathematics, the entropic risk measure is a risk measure which depends on the risk aversion of the user through the exponential utility function. This makes it a theoretically interesting measure because it would provide different risk values for different individuals...
.
Quantifying utility
It was recognized that utility could not be measured or observed directly, so instead economists devised a way to measure actual behavior and assume that, in a perfectly competitive equilibrium, this behavior reveals the underlying relative utilities. These 'revealed preferences', as they were named by Paul SamuelsonPaul Samuelson
Paul Anthony Samuelson was an American economist, and the first American to win the Nobel Memorial Prize in Economic Sciences. The Swedish Royal Academies stated, when awarding the prize, that he "has done more than any other contemporary economist to raise the level of scientific analysis in...
, were revealed in price:
Utility is taken to be correlative to Desire or Want. It has been already argued that desires cannot be measured directly, but only indirectly, by the outward phenomena to which they give rise: and that in those cases with which economics is chiefly concerned the measure is found in the price which a person is willing to pay for the fulfilment or satisfaction of his desire. (Marshall 1920:78)
Cardinal and ordinal utility
Economists distinguish between cardinal utilityCardinal utility
In economics, cardinal utility refers to a property of mathematical indices that preserve preference orderings uniquely up to positive linear transformations...
and ordinal utility
Ordinal utility
Ordinal utility theory states that while the utility of a particular good or service cannot be measured using a numerical scale bearing economic meaning in and of itself, pairs of alternative bundles of goods can be ordered such that one is considered by an individual to be worse than, equal to,...
. When cardinal utility is used, the magnitude of utility differences is treated as an ethically or behaviorally significant quantity. On the other hand, ordinal utility captures only ranking and not strength of preferences.
Utility functions of both sorts assign a ranking to members of a choice set. For example, suppose a cup of orange juice has utility of 120 utils, a cup of tea has a utility of 80 utils, and a cup of water has a utility of 40 utils. When speaking of cardinal utility, it could be concluded that the cup of orange juice is better than the cup of tea by exactly the same amount by which the cup of tea is better than the cup of water. One is not entitled to conclude, however, that the cup of tea is two thirds as good as the cup of juice, because this conclusion would depend not only on magnitudes of utility differences, but also on the "zero" of utility.
It is tempting when dealing with cardinal utility to aggregate utilities across persons. The argument against this is that interpersonal comparisons of utility are meaningless because there is no good way to interpret how different people value consumption bundles.
When ordinal utilities are used, differences in utils are treated as ethically or behaviorally meaningless: the utility index encode a full behavioral ordering between members of a choice set, but tells nothing about the related strength of preferences. In the above example, it would only be possible to say that juice is preferred to tea to water, but no more.
Neoclassical economics
Neoclassical economics
Neoclassical economics is a term variously used for approaches to economics focusing on the determination of prices, outputs, and income distributions in markets through supply and demand, often mediated through a hypothesized maximization of utility by income-constrained individuals and of profits...
has largely retreated from using cardinal utility functions as the basic objects of economic analysis, in favor of considering agent preference
Preference (economics)
In economics and other social sciences, preference refers to the set of assumptions related to ordering some alternatives, based on the degree of happiness, satisfaction, gratification, enjoyment, or utility they provide, a process which results in an optimal "choice"...
s over choice sets. However, preference relations can often be represented by utility functions satisfying several properties.
Ordinal utility functions are unique up to
Up to
In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
positive monotone transformations, while cardinal utilities are unique up to positive linear transformations.
Although preference
Preference
-Definitions in different disciplines:The term “preferences” is used in a variety of related, but not identical, ways in the scientific literature. This makes it necessary to make explicit the sense in which the term is used in different social sciences....
s are the conventional foundation of microeconomics
Microeconomics
Microeconomics is a branch of economics that studies the behavior of how the individual modern household and firms make decisions to allocate limited resources. Typically, it applies to markets where goods or services are being bought and sold...
, it is often convenient to represent preferences with a utility function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
and analyze human behavior indirectly with utility functions. Let X be the consumption set, the set of all mutually-exclusive baskets the consumer could conceivably consume. The consumer's utility function
ranks each package in the consumption set. If the consumer strictly prefers x to y or is indifferent between them, then u(x) > u(y).For example, suppose a consumer's consumption set is X = {nothing, 1 apple,1 orange, 1 apple and 1 orange, 2 apples, 2 oranges}, and its utility function is u(nothing) = 0, u(1 apple) = 1, u(1 orange) = 2, u(1 apple and 1 orange) = 4, u(2 apples) = 2 and u(2 oranges) = 3. Then this consumer prefers 1 orange to 1 apple, but prefers one of each to 2 oranges.
In microeconomic models, there are usually a finite set of L commodities, and a consumer may consume an arbitrary amount of each commodity. This gives a consumption set of
, and each package is a vector containing the amounts of each commodity. In the previous example, we might say there are two commodities: apples and oranges. If we say apples is the first commodity, and oranges the second, then the consumption set and u(0, 0) = 0, u(1, 0) = 1, u(0, 1) = 2, u(1, 1) = 4, u(2, 0) = 2, u(0, 2) = 3 as before. Note that for u to be a utility function on X, it must be defined for every package in X.A utility function
represents a preference relation on X iffIf and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
for every
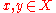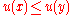, implies . If u represents , then this implies is complete and transitive, and hence rational.In order to simplify calculations, various assumptions have been made of utility functions.
- CESConstant Elasticity of SubstitutionIn economics, Constant elasticity of substitution is a property of some production functions and utility functions.More precisely, it refers to a particular type of aggregator function which combines two or more types of consumption, or two or more types of productive inputs into an aggregate...
(constant elasticity of substitution, or isoelastic) utility - Exponential utilityExponential utilityIn economics exponential discounting is a specific form of the discount function, used in the analysis of choice over time...
- Quasilinear utilityQuasilinear utilityIn economics and consumer theory, quasilinear utility functions are linear in one argument, generally the numeraire. This utility function has the representation U = x_1 + \theta...
- Homothetic preferencesHomothetic preferencesHomothetic preferences is a subset of preferences used in economics when analyzing the demand for consumption of various goods and services.In mathematics, a function of two or more arguments is homothetic if all ratios of its first partial derivatives depend only on the ratios of the arguments,...
Most utility functions used in modeling or theory are well-behaved. They are usually monotonic, quasi-concave, continuous and globally non-satiated. However, it is possible for preferences not to be representable by a utility function. An example is lexicographic preferences
Lexicographic preferences
Lexicographic preferences describe comparative preferences where an economic agent infinitely prefers one good to another . Thus if offered several bundles of goods, the agent will choose the bundle that offers the most X, no matter how much Y there is...
which are not continuous and cannot be represented by a continuous utility function.
Expected utility
The expected utility theory deals with the analysis of choices among risky projects with (possibly multidimensional) outcomes.The expected utility model was first proposed by Nicholas Bernoulli in 1713 and solved by Daniel Bernoulli
Daniel Bernoulli
Daniel Bernoulli was a Dutch-Swiss mathematician and was one of the many prominent mathematicians in the Bernoulli family. He is particularly remembered for his applications of mathematics to mechanics, especially fluid mechanics, and for his pioneering work in probability and statistics...
in 1738 as the St. Petersburg paradox
St. Petersburg paradox
In economics, the St. Petersburg paradox is a paradox related to probability theory and decision theory. It is based on a particular lottery game that leads to a random variable with infinite expected value, i.e., infinite expected payoff, but would nevertheless be considered to be worth only a...
. Bernoulli argued that the paradox could be resolved if decisionmakers displayed risk aversion
Risk aversion
Risk aversion is a concept in psychology, economics, and finance, based on the behavior of humans while exposed to uncertainty....
and argued for a logarithmic cardinal utility function.
The first important use of the expected utility theory was that of John von Neumann
John von Neumann
John von Neumann was a Hungarian-American mathematician and polymath who made major contributions to a vast number of fields, including set theory, functional analysis, quantum mechanics, ergodic theory, geometry, fluid dynamics, economics and game theory, computer science, numerical analysis,...
and Oskar Morgenstern
Oskar Morgenstern
Oskar Morgenstern was a German-born Austrian-School economist. He, along with John von Neumann, helped found the mathematical field of game theory ....
who used the assumption of expected utility maximization in their formulation of game theory
Game theory
Game theory is a mathematical method for analyzing calculated circumstances, such as in games, where a person’s success is based upon the choices of others...
.
Additive von Neumann–Morgenstern utility
When comparing objects it makes sense to rank utilities, but older conceptions of utility allowed no way to compare the sizes of utilities - a person may say that a new shirt is preferable to a baloney sandwich, but not that it is twenty times preferable to the sandwich.The reason is that the utility of twenty sandwiches is not twenty times the utility of one sandwich, by the law of diminishing returns. So it is hard to compare the utility of the shirt with 'twenty times the utility of the sandwich'. But Von Neumann and Morgenstern suggested an unambiguous way of making a comparison like this.
Their method of comparison involves considering probabilities. If a person can choose between various randomized events (lotteries), then it is possible to additively compare the shirt and the sandwich. It is possible to compare a sandwich with probability 1, to a shirt with probability p or nothing with probability 1 − p. By adjusting p, the point at which the sandwich becomes preferable defines the ratio of the utilities of the two options.
A notation for a lottery is as follows: if options A and B have probability p and 1 − p in the lottery, write it as a linear combination:
-
More generally, for a lottery with many possible options:
-
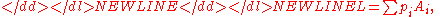
with the sum of the p is equalling 1.
By making some reasonable assumptions about the way choices behave, von Neumann and Morgenstern showed that if an agent can choose between the lotteries, then this agent has a utility function which can be added and multiplied by real numbers, which means the utility of an arbitrary lottery can be calculated as a linear combination of the utility of its parts.
This is called the expected utility theorem. The required assumptions are four axioms about the properties of the agent's preference relation over 'simple lotteries', which are lotteries with just two options. Writing
to mean 'A is preferred to B', the axioms are:
- completeness: For any two simple lotteries
and 
, either 
or 
(or both). - transitivity: for any three lotteries
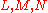, if 
and 
, then 
. - convexity/continuity (Archimedean property): If
, then there is a 
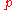between 0 and 1 such that the lottery 
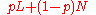is equally preferable to 
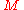. - independence: for any three lotteries
, 
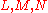if and only if 
.
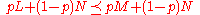In more formal language: A von Neumann–Morgenstern utility function is a function from choices to the real numbers:
which assigns a real number to every outcome in a way that captures the agent's preferences over simple lotteries. Under the four assumptions mentioned above, the agent will prefer a lottery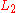
to a lottery 
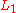if and only if the expected utility of 
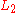is greater than the expected utility of 
:
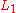Repeating in category language:
is a morphism between the category of preferences with uncertainty and the category of reals as an additive group.
Of all the axioms, independence is the most often discarded. A variety of generalized expected utilityGeneralized expected utilityThe expected utility model developed by John von Neumann and Oskar Morgenstern dominated decision theory from its formulation in 1944 until the late 1970s, not only as a prescriptive, but also as a descriptive model, despite powerful criticism from Maurice Allais and Daniel Ellsberg who showed...
theories have arisen, most of which drop or relax the independence axiom.
- CESConstant Elasticity of SubstitutionIn economics, Constant elasticity of substitution is a property of some production functions and utility functions.More precisely, it refers to a particular type of aggregator function which combines two or more types of consumption, or two or more types of productive inputs into an aggregate...
(constant elasticity of substitution, or isoelastic) utility is one with constant relative risk aversion - Exponential utilityExponential utilityIn economics exponential discounting is a specific form of the discount function, used in the analysis of choice over time...
exhibits constant absolute risk aversion
Money
One of the most common uses of a utility function, especially in economicsEconomicsEconomics is the social science that analyzes the production, distribution, and consumption of goods and services. The term economics comes from the Ancient Greek from + , hence "rules of the house"...
, is the utility of money. The utility function for money is a nonlinear function that is bounded and asymmetric about the origin. These properties can be derived from reasonable assumptions that are generally accepted by economists and decision theoristsDecision theoryDecision theory in economics, psychology, philosophy, mathematics, and statistics is concerned with identifying the values, uncertainties and other issues relevant in a given decision, its rationality, and the resulting optimal decision...
, especially proponents of rational choice theoryRational choice theoryRational choice theory, also known as choice theory or rational action theory, is a framework for understanding and often formally modeling social and economic behavior. It is the main theoretical paradigm in the currently-dominant school of microeconomics...
. The utility function is concaveConcave functionIn mathematics, a concave function is the negative of a convex function. A concave function is also synonymously called concave downwards, concave down, convex upwards, convex cap or upper convex.-Definition:...
in the positive region, reflecting the phenomenon of diminishing marginal utility. The boundedness reflects the fact that beyond a certain point money ceases being useful at all, as the size of any economy at any point in time is itself bounded. The asymmetry about the origin reflects the fact that gaining and losing money can have radically different implications both for individuals and businesses. The nonlinearity of the utility function for money has profound implications in decision making processes: in situations where outcomes of choices influence utility through gains or losses of money, which are the norm in most business settings, the optimal choice for a given decision depends on the possible outcomes of all other decisions in the same time-period.
Utility as probability of success
Castagnoli and LiCalzi (1996) and Bordley and LiCalzi (2000) provided another interpretation for Von Neumann and Morgenstern's theory. Specifically for any utility function, there exists a hypothetical reference lottery with the utility of a lottery being its probability of performing no worse than the reference lottery. Suppose success is defined as getting an outcome no worse than the outcome of the reference lottery. Then this mathematical equivalence means that maximizing expected utility is equivalent to maximizing the probability of success. In many contexts, this makes the concept of utility easier to justify and to apply. For example, a firm's utility might be the probability of meeting uncertain future customer expectations.
Discussion and criticism
Cambridge economist Joan RobinsonJoan RobinsonJoan Violet Robinson FBA was a post-Keynesian economist who was well known for her knowledge of monetary economics and wide-ranging contributions to economic theory...
famously criticized utility for being a circular concept: "Utility is the quality in commodities that makes individuals want to buy them, and the fact that individuals want to buy commodities shows that they have utility" (Robinson 1962: 48).
Different value systems have different perspectives on the use of utility in making moral judgments. For example, Marxists, Kantians, and certain libertariansLibertarianismLibertarianism, in the strictest sense, is the political philosophy that holds individual liberty as the basic moral principle of society. In the broadest sense, it is any political philosophy which approximates this view...
(such as Nozick) all believe utility to be irrelevant as a moral or at least not as important as other factors such as natural rightsRightsRights are legal, social, or ethical principles of freedom or entitlement; that is, rights are the fundamental normative rules about what is allowed of people or owed to people, according to some legal system, social convention, or ethical theory...
, law, conscience and/or religious doctrine. It is debatable whether any of these can be adequately represented in a system that uses a utility model.
Another criticism comes from the assertion that neither cardinal nor ordinary utility is empirically observable in the real world. In the case of cardinal utility it is impossible to measure the level of satisfaction "quantitatively" when someone consumes or purchases an apple. In case of ordinal utility, it is impossible to determine what choices were made when someone purchases, for example, an orange. Any act would involve preference over a vast setSetA set is a collection of well defined and distinct objects, considered as an object in its own right. Sets are one of the most fundamental concepts in mathematics. Developed at the end of the 19th century, set theory is now a ubiquitous part of mathematics, and can be used as a foundation from...
of choices (such as apple, orange juice, other vegetable, vitamin C tablets, exercise, not purchasing, etc.).
External links
- completeness: For any two simple lotteries
-
