Concave function
Encyclopedia
In mathematics
, a concave function is the negative
of a convex function
. A concave function is also synonym
ously called concave downwards, concave down, convex upwards, convex cap or upper convex.
f on an interval
(or, more generally, a convex set
in vector space
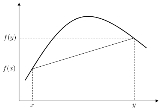
) is said to be concave if, for any x and y in the interval and for any t in [0,1],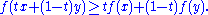
A function is called strictly concave if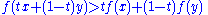
for any t in (0,1) and x ≠ y.
For a function f:R→R, this definition merely states that for every z between x and y, the point (z, f(z) ) on the graph of f is above the straight line joining the points (x, f(x) ) and (y, f(y) ).

A function f(x) is quasiconcave if the upper contour sets of the function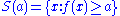 are convex sets.
are convex sets.
the function −f(x) is a convex function
over the set.
A differentiable function
f is concave on an interval
if its derivative
function f ′ is monotonically decreasing on that interval: a concave function has a decreasing slope
. ("Decreasing" here means "non-increasing", rather than "strictly decreasing", and thus allows zero slopes.)
For a twice-differentiable function f, if the second derivative
, f ′′(x), is positive (or, if the acceleration
is positive), then the graph is convex; if f ′′(x) is negative, then the graph is concave. Points
where concavity changes are inflection point
s.
If a convex (i.e., concave upward) function has a "bottom", any point
at the bottom is a minimal extremum
. If a concave (i.e., concave downward) function has an "apex", any point at the apex is a maximal extremum
.
If f(x) is twice-differentiable, then f(x) is concave if and only if
f ′′(x) is non-positive. If its second derivative is negative then it is strictly concave, but the opposite is not true, as shown by f(x) = -x4.
If f is concave and differentiable then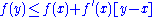
A continuous function
on C is concave if and only if
for any x and y in C
If a function f is concave, and f(0) ≥ 0, then f is subadditive. Proof:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a concave function is the negative
Additive inverse
In mathematics, the additive inverse, or opposite, of a number a is the number that, when added to a, yields zero.The additive inverse of a is denoted −a....
of a convex function
Convex function
In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
. A concave function is also synonym
Synonym
Synonyms are different words with almost identical or similar meanings. Words that are synonyms are said to be synonymous, and the state of being a synonym is called synonymy. The word comes from Ancient Greek syn and onoma . The words car and automobile are synonyms...
ously called concave downwards, concave down, convex upwards, convex cap or upper convex.
Definition
A real-valued functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
f on an interval
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
(or, more generally, a convex set
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
in vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
) is said to be concave if, for any x and y in the interval and for any t in [0,1],
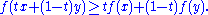
A function is called strictly concave if
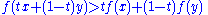
for any t in (0,1) and x ≠ y.
For a function f:R→R, this definition merely states that for every z between x and y, the point (z, f(z) ) on the graph of f is above the straight line joining the points (x, f(x) ) and (y, f(y) ).

A function f(x) is quasiconcave if the upper contour sets of the function
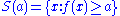 are convex sets.
are convex sets.Properties
A function f(x) is concave over a convex set if and only ifIf and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
the function −f(x) is a convex function
Convex function
In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
over the set.
A differentiable function
Graph of a function
In mathematics, the graph of a function f is the collection of all ordered pairs . In particular, if x is a real number, graph means the graphical representation of this collection, in the form of a curve on a Cartesian plane, together with Cartesian axes, etc. Graphing on a Cartesian plane is...
f is concave on an interval
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
if its derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
function f ′ is monotonically decreasing on that interval: a concave function has a decreasing slope
Slope
In mathematics, the slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline....
. ("Decreasing" here means "non-increasing", rather than "strictly decreasing", and thus allows zero slopes.)
For a twice-differentiable function f, if the second derivative
Second derivative
In calculus, the second derivative of a function ƒ is the derivative of the derivative of ƒ. Roughly speaking, the second derivative measures how the rate of change of a quantity is itself changing; for example, the second derivative of the position of a vehicle with respect to time is...
, f ′′(x), is positive (or, if the acceleration
Acceleration
In physics, acceleration is the rate of change of velocity with time. In one dimension, acceleration is the rate at which something speeds up or slows down. However, since velocity is a vector, acceleration describes the rate of change of both the magnitude and the direction of velocity. ...
is positive), then the graph is convex; if f ′′(x) is negative, then the graph is concave. Points
Point (geometry)
In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
where concavity changes are inflection point
Inflection point
In differential calculus, an inflection point, point of inflection, or inflection is a point on a curve at which the curvature or concavity changes sign. The curve changes from being concave upwards to concave downwards , or vice versa...
s.
If a convex (i.e., concave upward) function has a "bottom", any point
Point (geometry)
In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
at the bottom is a minimal extremum
Maxima and minima
In mathematics, the maximum and minimum of a function, known collectively as extrema , are the largest and smallest value that the function takes at a point either within a given neighborhood or on the function domain in its entirety .More generally, the...
. If a concave (i.e., concave downward) function has an "apex", any point at the apex is a maximal extremum
Maxima and minima
In mathematics, the maximum and minimum of a function, known collectively as extrema , are the largest and smallest value that the function takes at a point either within a given neighborhood or on the function domain in its entirety .More generally, the...
.
If f(x) is twice-differentiable, then f(x) is concave if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
f ′′(x) is non-positive. If its second derivative is negative then it is strictly concave, but the opposite is not true, as shown by f(x) = -x4.
If f is concave and differentiable then
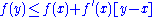
A continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
on C is concave if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
for any x and y in C

If a function f is concave, and f(0) ≥ 0, then f is subadditive. Proof:
- since f is concave, let y = 0,
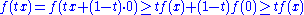
-
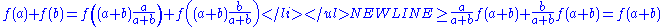
Examples
- The functions
 and
and 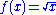 are concave, as the second derivative is always negative.
are concave, as the second derivative is always negative. - Any linear function
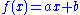 is both concave and convex.
is both concave and convex. - The function
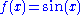 is concave on the interval
is concave on the interval 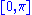 .
. - The function
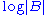 , where
, where 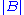 is the determinantDeterminantIn linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
is the determinantDeterminantIn linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of a nonnegative-definite matrix B, is concave. - Practical example: rays bending in Computation of radiowave attenuation in the atmosphereComputation of radiowave attenuation in the atmosphereOne of the causes of attenuation of radio propagation is the absorption by the atmosphere. There are many well known facts on the phenomenon and qualitative treatments in textbooks. A document published by the International Telecommunication Union...
.
See also
- Concave polygon
- Convex functionConvex functionIn mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
- Jensen's inequalityJensen's inequalityIn mathematics, Jensen's inequality, named after the Danish mathematician Johan Jensen, relates the value of a convex function of an integral to the integral of the convex function. It was proved by Jensen in 1906. Given its generality, the inequality appears in many forms depending on the context,...
- Logarithmically concave function
- Quasiconcave function
- The functions

