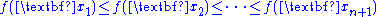Nelder-Mead method
Encyclopedia
| Nelder–Mead simplex search over the Rosenbrock banana function Rosenbrock function In mathematical optimization, the Rosenbrock function is a non-convex function used as a performance test problem for optimization algorithms introduced by Howard H. Rosenbrock in 1960. It is also known as Rosenbrock's valley or Rosenbrock's banana function.The global minimum is inside a long,... (above) and Himmelblau's function Himmelblau's function In mathematical optimization, the Himmelblau's function is a multi-modal function, used to test the performance of optimization algorithms.The function is defined by:... (below) |
|
- See simplex algorithmSimplex algorithmIn mathematical optimization, Dantzig's simplex algorithm is a popular algorithm for linear programming. The journal Computing in Science and Engineering listed it as one of the top 10 algorithms of the twentieth century....
for Dantzig's algorithm for the problem of linear optimizationLinear programmingLinear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...
.
The Nelder–Mead method or downhill simplex method or amoeba method is a commonly used nonlinear optimization
Optimization (mathematics)
In mathematics, computational science, or management science, mathematical optimization refers to the selection of a best element from some set of available alternatives....
technique, which is a well-defined numerical method for twice differentiable and unimodal problems. However, the Nelder–Mead technique is a heuristic
Heuristic
Heuristic refers to experience-based techniques for problem solving, learning, and discovery. Heuristic methods are used to speed up the process of finding a satisfactory solution, where an exhaustive search is impractical...
search method that can converge to non-stationary points on problems that can be solved by alternative methods.
The Nelder–Mead technique was proposed by John Nelder
John Nelder
John Ashworth Nelder FRS was a British statistician known for his contributions to experimental design, analysis of variance, computational statistics, and statistical theory.-Contributions:...
& Roger Mead (1965) and is a technique for minimizing an objective function in a many-dimensional space
Space
Space is the boundless, three-dimensional extent in which objects and events occur and have relative position and direction. Physical space is often conceived in three linear dimensions, although modern physicists usually consider it, with time, to be part of a boundless four-dimensional continuum...
.
Overview
The method uses the concept of a simplexSimplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
, which is a special polytope
Polytope
In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...
of N + 1 vertices in N dimensions. Examples of simplices include a line segment on a line, a triangle on a plane, a tetrahedron
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
in three-dimensional space and so forth.
The method approximates a local optimum of a problem with N variables when the objective function varies smoothly and is unimodal.
For example, a suspension bridge engineer has to choose how thick each strut, cable, and pier must be. Clearly these all link together, but it is not easy to visualize the impact of changing any specific element. The engineer can use the Nelder–Mead method to generate trial designs which are then tested on a large computer model. As each run of the simulation is expensive, it is important to make good decisions about where to look.
Nelder–Mead generates a new test position by extrapolating the behavior of the objective function measured at each test point arranged as a simplex. The algorithm then chooses to replace one of these test points with the new test point and so the technique progresses. The simplest step is to replace the worst point with a point reflected through the centroid
Centroid
In geometry, the centroid, geometric center, or barycenter of a plane figure or two-dimensional shape X is the intersection of all straight lines that divide X into two parts of equal moment about the line. Informally, it is the "average" of all points of X...
of the remaining N points. If this point is better than the best current point, then we can try stretching exponentially out along this line. On the other hand, if this new point isn't much better than the previous value, then we are stepping across a valley, so we shrink the simplex towards a better point.
Unlike modern optimization methods, the Nelder–Mead heuristic can converge to a non-stationary point unless the problem satisfies stronger conditions than are necessary for modern methods. Modern improvements over the Nelder–Mead heuristic have been known since 1979.
Many variations exist depending on the actual nature of the problem being solved. A common variant uses a constant-size, small simplex that roughly follows the gradient direction (which gives steepest descent). Visualize a small triangle on an elevation map flip-flopping its way down a valley to a local bottom. This method is also known as the Flexible Polyhedron Method. This, however, tends to perform poorly against the method described in this article because it makes small, unnecessary steps in areas of little interest.
One possible variation of the NM algorithm
- 1. Order according to the values at the vertices:
- 2. Calculate
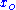 , the center of gravity of all points except
, the center of gravity of all points except 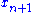 .
.
- 3. Reflection
-
- Compute reflected point
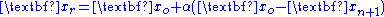
- If the reflected point is better than the second worst, but not better than the best, i.e.:
 ,
, - then obtain a new simplex by replacing the worst point
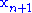 with the reflected point
with the reflected point 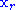 , and go to step 1.
, and go to step 1.
- Compute reflected point
- 4. Expansion
-
- If the reflected point is the best point so far,

- then compute the expanded point

- If the expanded point is better than the reflected point,

- then obtain a new simplex by replacing the worst point
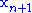 with the expanded point
with the expanded point  , and go to step 1.
, and go to step 1. - Else obtain a new simplex by replacing the worst point
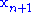 with the reflected point
with the reflected point 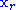 , and go to step 1.
, and go to step 1.
- If the expanded point is better than the reflected point,
- Else (i.e. reflected point is not better than second worst) continue at step 5.
- If the reflected point is the best point so far,
- 5. Contraction
-
- Here, it is certain that
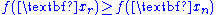
- Compute contracted point
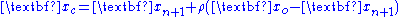
- If the contracted point is better than the worst point, i.e.

- then obtain a new simplex by replacing the worst point
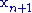 with the contracted point
with the contracted point 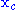 , and go to step 1.
, and go to step 1.
- If the contracted point is better than the worst point, i.e.
- Else go to step 6.
- Here, it is certain that
- 6. Reduction
-
- For all but the best point, replace the point with
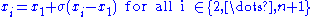 . go to step 1.
. go to step 1.
Note:
 ,
, 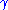 ,
,  and
and  are respectively the reflection, the expansion, the contraction and the shrink coefficient. Standard values are
are respectively the reflection, the expansion, the contraction and the shrink coefficient. Standard values are  ,
,  ,
, 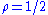 and
and 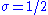 .
.For the reflection, since
 is the vertex with the higher associated value among the vertices, we can expect to find a lower value at the reflection of
is the vertex with the higher associated value among the vertices, we can expect to find a lower value at the reflection of 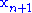 in the opposite face formed by all vertices point
in the opposite face formed by all vertices point  except
except  .
.For the expansion, if the reflection point
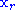 is the new minimum along the vertices we can expect to find interesting values along the direction from
is the new minimum along the vertices we can expect to find interesting values along the direction from  to
to  .
.Concerning the contraction: If
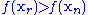 we can expect that a better value will be inside the simplex formed by all the vertices
we can expect that a better value will be inside the simplex formed by all the vertices  .
.The initial simplex is important, indeed, a too small initial simplex can lead to a local search, consequently the NM can get more easily stuck. So this simplex should depend on the nature of the problem.
See also
- Conjugate gradient methodConjugate gradient methodIn mathematics, the conjugate gradient method is an algorithm for the numerical solution of particular systems of linear equations, namely those whose matrix is symmetric and positive-definite. The conjugate gradient method is an iterative method, so it can be applied to sparse systems that are too...
- Levenberg–Marquardt algorithm
- Broyden–Fletcher–Goldfarb–Shanno or BFGS methodBFGS methodIn numerical optimization, the Broyden–Fletcher–Goldfarb–Shanno method is a method for solving nonlinear optimization problems ....
- Differential evolutionDifferential evolutionIn computer science, differential evolution is a method that optimizes a problem by iteratively trying to improve a candidate solution with regard to a given measure of quality. Such methods are commonly known as metaheuristics as they make few or no assumptions about the problem being optimized...
Further reading
- Avriel, Mordecai (2003). Nonlinear Programming: Analysis and Methods. Dover Publishing. ISBN 0-486-43227-0.
- Coope, I. D.; C.J. Price, 2002. “Positive bases in numerical optimization”, Computational Optimization & Applications, Vol. 21, No. 2, pp. 169–176, 2002.
External links
- Nelder–Mead (Simplex) Method
- Nelder–Mead Search for a Minimum
- John Burkardt: Nelder–Mead code in Matlab - note that a variation of the Nelder-Mead method is also implemented by the Matlab function fminsearch.
- Nelder–Mead online for the calibration of the SABR model - Application in Finance.