
Arg max
Encyclopedia
In mathematics
, arg max stands for the argument of the maximum, that is to say, the set of points of the given argument
for which the given function
attains its maximum value
:For clarity, we refer to the input (x) as points and the output (y) as values; compare critical point
and critical value
.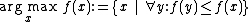
In other words,

is the set of values of x for which f(x) attains its largest value M. For example, if f(x) is 1−|x|, then it attains its maximum value of 1 at x = 0 and only there, so .
.
Equivalently, if M is the maximum of f, then the arg max is the level set
of the maximum: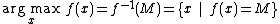
If the maximum is reached at a single value, then one refers to the point as the arg max, meaning we define the arg max as a point, not a set of points. So, for example,

(rather than the singleton set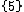 ), since the maximum value of x(10 − x) is 25, which occurs for x = 5.By differentiation, we have
), since the maximum value of x(10 − x) is 25, which occurs for x = 5.By differentiation, we have 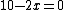 .
.
However, in case the maximum is reached at many values, arg max is a set of points.
Then, we have for example
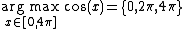
since the maximum value of cos(x) is 1, which occurs on this interval for
x = 0, 2π or 4π. On the whole real line, the arg max is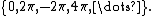
Note also that functions do not in general attain a maximum value, and hence will in general not have an arg max: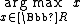 is undefined, as x is unbounded on the real line. However, by the extreme value theorem
is undefined, as x is unbounded on the real line. However, by the extreme value theorem
(or the classical compactness argument), a continuous function on a compact
interval
has a maximum, and thus an arg max.
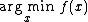
are values of x for which f(x) attains its smallest value M.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, arg max stands for the argument of the maximum, that is to say, the set of points of the given argument
Argument of a function
In mathematics, an argument of a function is a specific input in the function, also known as an independent variable. When it is clear from the context which argument is meant, the argument is often denoted by arg....
for which the given function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
attains its maximum value
Value (mathematics)
In mathematics, value commonly refers to the 'output' of a function. In the most basic case, that of unary, single-valued functions, there is one input and one output .The function f of the example is real-valued, since each and every possible function value is real...
:For clarity, we refer to the input (x) as points and the output (y) as values; compare critical point
Critical point (mathematics)
In calculus, a critical point of a function of a real variable is any value in the domain where either the function is not differentiable or its derivative is 0. The value of the function at a critical point is a critical value of the function...
and critical value
Critical value
-Differential topology:In differential topology, a critical value of a differentiable function between differentiable manifolds is the image ƒ in N of a critical point x in M.The basic result on critical values is Sard's lemma...
.
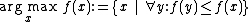
In other words,

is the set of values of x for which f(x) attains its largest value M. For example, if f(x) is 1−|x|, then it attains its maximum value of 1 at x = 0 and only there, so
 .
.Equivalently, if M is the maximum of f, then the arg max is the level set
Level set
In mathematics, a level set of a real-valued function f of n variables is a set of the formthat is, a set where the function takes on a given constant value c....
of the maximum:
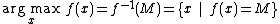
If the maximum is reached at a single value, then one refers to the point as the arg max, meaning we define the arg max as a point, not a set of points. So, for example,

(rather than the singleton set
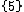 ), since the maximum value of x(10 − x) is 25, which occurs for x = 5.By differentiation, we have
), since the maximum value of x(10 − x) is 25, which occurs for x = 5.By differentiation, we have 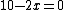 .
.However, in case the maximum is reached at many values, arg max is a set of points.
Then, we have for example
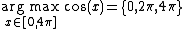
since the maximum value of cos(x) is 1, which occurs on this interval for
x = 0, 2π or 4π. On the whole real line, the arg max is
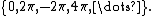
Note also that functions do not in general attain a maximum value, and hence will in general not have an arg max:
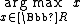 is undefined, as x is unbounded on the real line. However, by the extreme value theorem
is undefined, as x is unbounded on the real line. However, by the extreme value theoremExtreme value theorem
In calculus, the extreme value theorem states that if a real-valued function f is continuous in the closed and bounded interval [a,b], then f must attain its maximum and minimum value, each at least once...
(or the classical compactness argument), a continuous function on a compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
interval
Interval
Interval may refer to:* Interval , a range of numbers * Interval measurements or interval variables in statistics is a level of measurement...
has a maximum, and thus an arg max.
Arg min
arg min stands for argument of the minimum, and are defined analogously. For instance,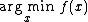
are values of x for which f(x) attains its smallest value M.
See also
- Argument of a functionArgument of a functionIn mathematics, an argument of a function is a specific input in the function, also known as an independent variable. When it is clear from the context which argument is meant, the argument is often denoted by arg....
- Maxima and minimaMaxima and minimaIn mathematics, the maximum and minimum of a function, known collectively as extrema , are the largest and smallest value that the function takes at a point either within a given neighborhood or on the function domain in its entirety .More generally, the...
- Mode (statistics)Mode (statistics)In statistics, the mode is the value that occurs most frequently in a data set or a probability distribution. In some fields, notably education, sample data are often called scores, and the sample mode is known as the modal score....
- Mathematical optimization

