Nonlinear programming
Encyclopedia
In mathematics
, nonlinear programming (NLP) is the process of solving a system of equalities
and inequalities, collectively termed constraints, over a set of unknown real variables, along with an objective function
to be maximized or minimized, where some of the constraints or the objective function are nonlinear.
 to maximize some variable such as product throughput
to maximize some variable such as product throughput
or to minimize a cost function
to minimize a cost function
where

is a polytope
, the problem is a linear programming
problem, which may be solved using well known linear programming solutions.
If the objective function is concave
(maximization problem), or convex
(minimization problem) and the constraint set is convex
, then the program is called convex and general methods from convex optimization can be used in most cases.
If the objective function is a ratio of a concave and a convex function (in the maximization case) and the constraints are convex, then the problem can be transformed to a convex optimization problem using fractional programming
techniques.
Several methods are available for solving nonconvex problems. One approach is to use special formulations of linear programming problems. Another method involves the use of branch and bound
techniques, where the program is divided into subclasses to be solved with convex (minimization problem) or linear approximations that form a lower bound on the overall cost within the subdivision. With subsequent divisions, at some point an actual solution will be obtained whose cost is equal to the best lower bound obtained for any of the approximate solutions. This solution is optimal, although possibly not unique. The algorithm may also be stopped early, with the assurance that the best possible solution is within a tolerance from the best point found; such points are called ε-optimal. Terminating to ε-optimal points is typically necessary to ensure finite termination. This is especially useful for large, difficult problems and problems with uncertain costs or values where the uncertainty can be estimated with an appropriate reliability estimation.
Under differentiability and constraint qualifications, the Karush–Kuhn–Tucker (KKT) conditions provide necessary conditions for a solution to be optimal. Under convexity, these conditions are also sufficient.
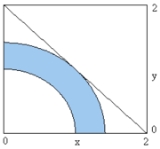
 A simple problem can be defined by the constraints
A simple problem can be defined by the constraints
with an objective function to be maximized
where x = (x1, x2). Solve 2-D Problem.
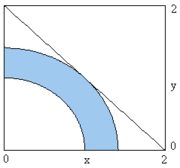
 Another simple problem can be defined by the constraints
Another simple problem can be defined by the constraints
with an objective function to be maximized
where x = (x1, x2, x3). Solve 3-D Problem.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, nonlinear programming (NLP) is the process of solving a system of equalities
Equation
An equation is a mathematical statement that asserts the equality of two expressions. In modern notation, this is written by placing the expressions on either side of an equals sign , for examplex + 3 = 5\,asserts that x+3 is equal to 5...
and inequalities, collectively termed constraints, over a set of unknown real variables, along with an objective function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
to be maximized or minimized, where some of the constraints or the objective function are nonlinear.
Applicability
A typical nonconvex problem is that of optimising transportation costs by selection from a set of transportion methods, one or more of which exhibit economies of scale, with various connectivities and capacity constraints. An example would be petroleum product transport given a selection or combination of pipeline, rail tanker, road tanker, river barge, or coastal tankship. Owing to economic batch size the cost functions may have discontinuities in addition to smooth changes.Mathematical formulation of the problem
The problem can be stated simply as: to maximize some variable such as product throughput
to maximize some variable such as product throughputor
 to minimize a cost function
to minimize a cost functionwhere


Methods for solving the problem
If the objective function f is linear and the constrained spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
is a polytope
Polytope
In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...
, the problem is a linear programming
Linear programming
Linear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...
problem, which may be solved using well known linear programming solutions.
If the objective function is concave
Concave function
In mathematics, a concave function is the negative of a convex function. A concave function is also synonymously called concave downwards, concave down, convex upwards, convex cap or upper convex.-Definition:...
(maximization problem), or convex
Convex function
In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
(minimization problem) and the constraint set is convex
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
, then the program is called convex and general methods from convex optimization can be used in most cases.
If the objective function is a ratio of a concave and a convex function (in the maximization case) and the constraints are convex, then the problem can be transformed to a convex optimization problem using fractional programming
Fractional programming
In mathematical optimization, fractional programming is a generalization of linear-fractional programming. The objective function in a fractional program is a ratio of two functions that are in general nonlinear...
techniques.
Several methods are available for solving nonconvex problems. One approach is to use special formulations of linear programming problems. Another method involves the use of branch and bound
Branch and bound
Branch and bound is a general algorithm for finding optimal solutions of various optimization problems, especially in discrete and combinatorial optimization...
techniques, where the program is divided into subclasses to be solved with convex (minimization problem) or linear approximations that form a lower bound on the overall cost within the subdivision. With subsequent divisions, at some point an actual solution will be obtained whose cost is equal to the best lower bound obtained for any of the approximate solutions. This solution is optimal, although possibly not unique. The algorithm may also be stopped early, with the assurance that the best possible solution is within a tolerance from the best point found; such points are called ε-optimal. Terminating to ε-optimal points is typically necessary to ensure finite termination. This is especially useful for large, difficult problems and problems with uncertain costs or values where the uncertainty can be estimated with an appropriate reliability estimation.
Under differentiability and constraint qualifications, the Karush–Kuhn–Tucker (KKT) conditions provide necessary conditions for a solution to be optimal. Under convexity, these conditions are also sufficient.
2-dimensional example

- x1 ≥ 0
- x2 ≥ 0
- x12 + x22 ≥ 1
- x12 + x22 ≤ 2
with an objective function to be maximized
- f(x) = x1 + x2
where x = (x1, x2). Solve 2-D Problem.
3-dimensional example

- x12 − x22 + x32 ≤ 2
- x12 + x22 + x32 ≤ 10
with an objective function to be maximized
- f(x) = x1x2 + x2x3
where x = (x1, x2, x3). Solve 3-D Problem.
See also
- Curve fittingCurve fittingCurve fitting is the process of constructing a curve, or mathematical function, that has the best fit to a series of data points, possibly subject to constraints. Curve fitting can involve either interpolation, where an exact fit to the data is required, or smoothing, in which a "smooth" function...
- Least squaresLeast squaresThe method of least squares is a standard approach to the approximate solution of overdetermined systems, i.e., sets of equations in which there are more equations than unknowns. "Least squares" means that the overall solution minimizes the sum of the squares of the errors made in solving every...
minimization - Linear programmingLinear programmingLinear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...
- nl (format)Nl (format)nl is a file format for presenting and archiving mathematical programming problems. It supports linear and nonlinear optimization problems as well as complementarity problems , in discrete or continuous variables...
- Mathematical optimization
- List of optimization software
Further reading
- Avriel, Mordecai (2003). Nonlinear Programming: Analysis and Methods. Dover Publishing. ISBN 0-486-43227-0.
- Bazaraa, Mokhtar S. and Shetty, C. M. (1979). Nonlinear programming. Theory and algorithms. John Wiley & Sons. ISBN 0-471-78610-1.
- Bertsekas, Dimitri P. (1999). Nonlinear Programming: 2nd Edition. Athena Scientific. ISBN 1-886529-00-0.
- Nocedal, Jorge and Wright, Stephen J. (1999). Numerical Optimization. Springer. ISBN 0-387-98793-2.
- Jan BrinkhuisJan BrinkhuisProf. dr. Jan Brinkhuis is Associate Professor of Finance and Mathematical Methods and Techniques at the Econometric Institute of Erasmus University Rotterdam, Rotterdam. He obtained his PhD in 1981 with the disseration "Embedding Problems and Galois Modules"...
and Vladimir Tikhomirov, 'Optimization: Insights and Applications', 2005, Princeton University Press

