
Constraint (mathematics)
Encyclopedia
In mathematics
, a constraint is a condition that a solution to an optimization
problem must satisfy. There are two types of constraints: equality constraints and inequality constraints. The set of solutions that satisfy all constraints is called the feasible set
.
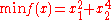
subject to
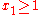
and

where denotes the vector
denotes the vector
(x1, x2).
In this example, the first line defines the function to be minimized (called the objective or cost function). The second and third lines define two constraints, the first of which is an inequality constraint and the second is an equality constraint. These two constraints define the feasible set of candidate solution
s.
Without the constraints, the solution would be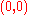 where
where 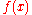 has the lowest value. But this solution does not satisfy the constraints. The solution of the constrained optimization problem stated above but
has the lowest value. But this solution does not satisfy the constraints. The solution of the constrained optimization problem stated above but  , which is the point with the smallest value of
, which is the point with the smallest value of 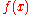 that satisfies the two constraints.
that satisfies the two constraints.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a constraint is a condition that a solution to an optimization
Optimization (mathematics)
In mathematics, computational science, or management science, mathematical optimization refers to the selection of a best element from some set of available alternatives....
problem must satisfy. There are two types of constraints: equality constraints and inequality constraints. The set of solutions that satisfy all constraints is called the feasible set
Candidate solution
In optimization , a candidate solution is a member of a set of possible solutions to a given problem. A candidate solution does not have to be a likely or reasonable solution to the problem – it is simply in the set that satisfies all constraints.The space of all candidate solutions is called the...
.
Example
The following is a simple optimization problem: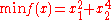
subject to
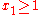
and

where
 denotes the vector
denotes the vectorVectorization (mathematics)
In mathematics, especially in linear algebra and matrix theory, the vectorization of a matrix is a linear transformation which converts the matrix into a column vector...
(x1, x2).
In this example, the first line defines the function to be minimized (called the objective or cost function). The second and third lines define two constraints, the first of which is an inequality constraint and the second is an equality constraint. These two constraints define the feasible set of candidate solution
Candidate solution
In optimization , a candidate solution is a member of a set of possible solutions to a given problem. A candidate solution does not have to be a likely or reasonable solution to the problem – it is simply in the set that satisfies all constraints.The space of all candidate solutions is called the...
s.
Without the constraints, the solution would be
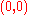 where
where 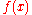 has the lowest value. But this solution does not satisfy the constraints. The solution of the constrained optimization problem stated above but
has the lowest value. But this solution does not satisfy the constraints. The solution of the constrained optimization problem stated above but  , which is the point with the smallest value of
, which is the point with the smallest value of 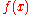 that satisfies the two constraints.
that satisfies the two constraints.Terminology
- If a constraint is an equality at a given point, the constraint is said to be , as the point cannot be varied in the direction of the constraint.
- If a constraint is an inequality at a given point, the constraint is said to be , as the point can be varied in the direction of the constraint.
- If a constraint is not satisfied, the point is said to be infeasible.
See also
- Constraint satisfaction problemConstraint satisfaction problemConstraint satisfaction problems s are mathematical problems defined as a set of objects whose state must satisfy a number of constraints or limitations. CSPs represent the entities in a problem as a homogeneous collection of finite constraints over variables, which is solved by constraint...
- Karush–Kuhn–Tucker conditions
- Lagrange multipliersLagrange multipliersIn mathematical optimization, the method of Lagrange multipliers provides a strategy for finding the maxima and minima of a function subject to constraints.For instance , consider the optimization problem...
- Level setLevel setIn mathematics, a level set of a real-valued function f of n variables is a set of the formthat is, a set where the function takes on a given constant value c....
- Linear programmingLinear programmingLinear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...
- Nonlinear programmingNonlinear programmingIn mathematics, nonlinear programming is the process of solving a system of equalities and inequalities, collectively termed constraints, over a set of unknown real variables, along with an objective function to be maximized or minimized, where some of the constraints or the objective function are...

