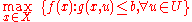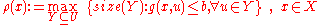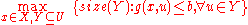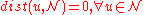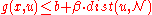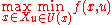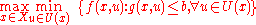Robust optimization
Encyclopedia
Robust optimization is a field of optimization
theory that deals with optimization problems where robustness is sought against uncertainty
and/or variability in the value of a parameter of the problem.
in the 1950s and the use of worst case analysis and Wald's maximin model
as a tool for the treatment of severe uncertainty. It became a field of its own in the 1970s with parallel developments in fields such as operations research
, control theory
, statistics
, economics
, and more.
problem
where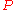
is a given subset of 
.
What makes this a 'robust optimization' problem is the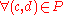
clause in the constraints. Its implication is that for a pair 
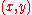to be admissible, the constraint 
must be satisfied by the worst 
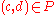pertaining to 
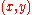, namely the pair 
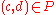that maximizes the value of 
for the given value of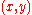 
.
If the parameter space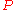
is finite (consisting of finitely many elements), then this robust optimization problem itself is a linear programming
problem: for each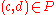
there is a linear constraint 
.
If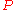
is not a finite set, then this problem is a linear semi-infinite programming problem, namely a linear programming problem with finitely many (2) decision variables and infinitely many constraints.
oriented and as such usually deploy Wald's maximin models
.
model:
where
denotes the nominal value of the parameter, 
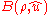denotes a ball of radius 
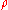centered at 
and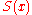 
denotes the set of values of 
that satisfy given stability/performance conditions associated with decision 
.
In words, the robustness (radius of stability) of decision
is the radius of the largest ball centered at 
all of whose elements satisfy the stability requirements imposed on 
. The picture is this:
where the rectangle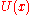
represents the set of all the values 
associated with decision 
.
where
denotes the set of all possible values of 
under consideration.
This is a global robust optimization problem in the sense that the robustness constraint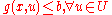
represents all the possible values of 
.
The difficulty is that such a "global" constraint can be too demanding in that there is no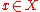
that satisfies this constraint. But even if such an 
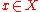exists, the constraint can be too "conservative" in that it yields a solution 
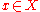that generates a very small payoff 
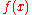that is not representative of the performance of other decisions in 
. For instance, there could be an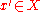 
that only slightly violates the robustness constraint but yields a very large payoff 
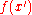. In such cases it might be necessary to relax a bit the robustness constraint and/or modify the statement of the problem.
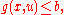. where 
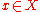denotes the decision variable and 
is a parameter whose set of possible values in 
. If there is no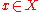 
such that 
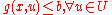, then the following intuitive measure of robustness suggests itself:
where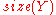
denotes an appropriate measure of the "size" of set 
. For example, if 
is a finite set, then 
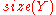could be defined as the cardinality of set 
.
In words, the robustness of decision is the size of the largest subset of
for which the constraint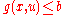 
is satisfied for each 
in this set. An optimal decision is then a decision whose robustness is the largest.
This yields the following robust optimization problem:
This intuitive notion of global robustness is not used often in practice because the robust optimization problems that it induces are usually (not always) very difficult to solve.
where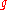
is a real-valued function on 
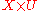, and assume that there is no feasible solution to this problem because the robustness constraint 
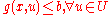is too demanding.
To overcome this difficult, let
be a relatively small subset of 
representing "normal" values of 
and consider the following robust optimization problem: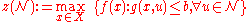
Since
is much smaller than 
, its optimal solution may not perform well on a large portion of 
and therefore may not be robust against the variability of 
over 
.
One way to fix this difficulty is to relax the constraint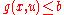
for values of 
outside the set 
in a controlled manner so that larger violations are allowed as the distance of 
from 
increases. For instance, consider the relaxed robustness constraint
where
is a control parameter and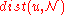 
denotes the distance of 
from 
. Thus, for 
the relaxed robustness constraint reduces back to the original robustness constraint.
This yields the following (relaxed) robust optimization problem:
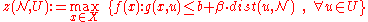
The function
is defined in such a manner that
and
and therefore the optimal solution to the relaxed problem satisfies the original constraint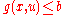
for all values of 
in 
. In addition, it also satisfies the relaxed constraint
outside
.
, namely
where the
represents the decision maker, the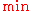 
represents Nature, namely uncertainty
,
represents the decision space and 
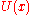denotes the set of possible values of 
associated with decision 
. This is the classic format of the generic model, and is often referred to as minimax or maximin optimization problem. The non-probabilistic (deterministic) model has been and is being extensively used for robust optimization especially in the field of signal processing .
The equivalent mathematical programming
(MP) of the classic format above is
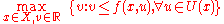
Constraints can be incorporated explicitly in these models. The generic constrained classic format is
The equivalent constrained MP format is
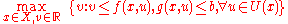
In another effort and in one of the non-probabilistic models, Erfani and Utyuzhnikov , use the fuzzy variables in order to quantify the uncertainties within the design parameters. They introduce a Robust measure in context of multiobjective optimization
to find the robust Pareto optimal solutions.
and stochastic optimization
models.
Optimization (mathematics)
In mathematics, computational science, or management science, mathematical optimization refers to the selection of a best element from some set of available alternatives....
theory that deals with optimization problems where robustness is sought against uncertainty
Uncertainty
Uncertainty is a term used in subtly different ways in a number of fields, including physics, philosophy, statistics, economics, finance, insurance, psychology, sociology, engineering, and information science...
and/or variability in the value of a parameter of the problem.
History
The origins of robust optimization date back to the establishment of modern decision theoryDecision theory
Decision theory in economics, psychology, philosophy, mathematics, and statistics is concerned with identifying the values, uncertainties and other issues relevant in a given decision, its rationality, and the resulting optimal decision...
in the 1950s and the use of worst case analysis and Wald's maximin model
Wald's maximin model
In decision theory and game theory, Wald's maximin model is a non-probabilistic decision-making model according to which decisions are ranked on the basis of their worst-case outcomes. That is, the best decision is one whose worst outcome is at least as good as the worst outcome of any other...
as a tool for the treatment of severe uncertainty. It became a field of its own in the 1970s with parallel developments in fields such as operations research
Operations research
Operations research is an interdisciplinary mathematical science that focuses on the effective use of technology by organizations...
, control theory
Control theory
Control theory is an interdisciplinary branch of engineering and mathematics that deals with the behavior of dynamical systems. The desired output of a system is called the reference...
, statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, economics
Economics
Economics is the social science that analyzes the production, distribution, and consumption of goods and services. The term economics comes from the Ancient Greek from + , hence "rules of the house"...
, and more.
Example
Consider the simple linear programmingLinear programming
Linear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...
problem
where
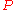is a given subset of .What makes this a 'robust optimization' problem is the
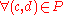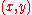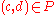clause in the constraints. Its implication is that for a pair to be admissible, the constraint must be satisfied by the worst pertaining to 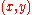, namely the pair 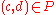that maximizes the value of for the given value of 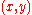.If the parameter space
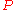is finite (consisting of finitely many elements), then this robust optimization problem itself is a linear programmingLinear programming
Linear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...
problem: for each
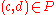there is a linear constraint .If
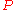is not a finite set, then this problem is a linear semi-infinite programming problem, namely a linear programming problem with finitely many (2) decision variables and infinitely many constraints.Classification
There are a number of classification criteria for robust optimization problems/models. In particular, one can distinguish between problems dealing with local and global models of robustness; and between probabilistic and non-probabilistic models of robustness. Modern robust optimization deals primarily with non-probabilistic models of robustness that are worst caseWorst Case
Worst Case is the 3rd book in the Michael Bennett series from James Patterson and Michael Ledwidge.-Plot summary:NYPD Detective Mike Bennett and his new partner FBI Special Agent Emily Parker are on the trail of Francis Mooney, a Manhattan trusts and estates lawyer with terminal lung cancer...
oriented and as such usually deploy Wald's maximin models
Wald's maximin model
In decision theory and game theory, Wald's maximin model is a non-probabilistic decision-making model according to which decisions are ranked on the basis of their worst-case outcomes. That is, the best decision is one whose worst outcome is at least as good as the worst outcome of any other...
.
Local robustness
There are cases where robustness is sought against small perturbations in a nominal value of a parameter. A very popular model of local robustness is the radius of stabilityStability radius
The stability radius of an object at a given nominal point is the radius of the largest ball, centered at the nominal point, all whose elements satisfy pre-determined stability conditions...
model:
where
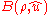denotes the nominal value of the parameter, denotes a ball of radius 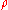centered at and 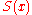denotes the set of values of that satisfy given stability/performance conditions associated with decision .In words, the robustness (radius of stability) of decision
is the radius of the largest ball centered at all of whose elements satisfy the stability requirements imposed on . The picture is this:where the rectangle
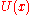represents the set of all the values associated with decision .Global robustness
Consider the simple abstract robust optimization problem
where
denotes the set of all possible values of under consideration.This is a global robust optimization problem in the sense that the robustness constraint
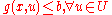represents all the possible values of .The difficulty is that such a "global" constraint can be too demanding in that there is no
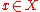that satisfies this constraint. But even if such an 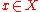exists, the constraint can be too "conservative" in that it yields a solution 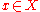that generates a very small payoff 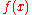that is not representative of the performance of other decisions in . For instance, there could be an 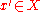that only slightly violates the robustness constraint but yields a very large payoff 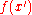. In such cases it might be necessary to relax a bit the robustness constraint and/or modify the statement of the problem.Example
Consider the case where the objective is to satisfy a constraint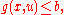. where 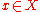denotes the decision variable and is a parameter whose set of possible values in . If there is no 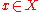such that 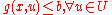, then the following intuitive measure of robustness suggests itself:
where
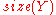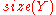denotes an appropriate measure of the "size" of set . For example, if is a finite set, then could be defined as the cardinality of set .In words, the robustness of decision is the size of the largest subset of
for which the constraint 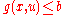is satisfied for each in this set. An optimal decision is then a decision whose robustness is the largest.This yields the following robust optimization problem:
This intuitive notion of global robustness is not used often in practice because the robust optimization problems that it induces are usually (not always) very difficult to solve.
Example
Consider the robust optimization problemwhere
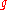is a real-valued function on 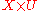, and assume that there is no feasible solution to this problem because the robustness constraint 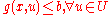is too demanding.To overcome this difficult, let
be a relatively small subset of representing "normal" values of and consider the following robust optimization problem: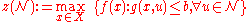Since
is much smaller than , its optimal solution may not perform well on a large portion of and therefore may not be robust against the variability of over .One way to fix this difficulty is to relax the constraint
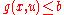for values of outside the set in a controlled manner so that larger violations are allowed as the distance of from increases. For instance, consider the relaxed robustness constraint
where
is a control parameter and 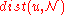denotes the distance of from . Thus, for the relaxed robustness constraint reduces back to the original robustness constraint.This yields the following (relaxed) robust optimization problem:
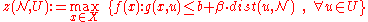
The function
is defined in such a manner thatand
and therefore the optimal solution to the relaxed problem satisfies the original constraint
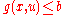for all values of in . In addition, it also satisfies the relaxed constraint
outside
.Non-probabilistic robust optimization models
The dominating paradigm in this area of robust optimization is Wald's maximin modelWald's maximin model
In decision theory and game theory, Wald's maximin model is a non-probabilistic decision-making model according to which decisions are ranked on the basis of their worst-case outcomes. That is, the best decision is one whose worst outcome is at least as good as the worst outcome of any other...
, namely
where the
represents the decision maker, the 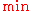represents Nature, namely uncertaintyUncertainty
Uncertainty is a term used in subtly different ways in a number of fields, including physics, philosophy, statistics, economics, finance, insurance, psychology, sociology, engineering, and information science...
,
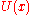represents the decision space and denotes the set of possible values of associated with decision . This is the classic format of the generic model, and is often referred to as minimax or maximin optimization problem. The non-probabilistic (deterministic) model has been and is being extensively used for robust optimization especially in the field of signal processing .The equivalent mathematical programming
Mathematical Programming
Mathematical Programming, established in 1971, and published by Springer Science+Business Media, is the official scientific journal of the Mathematical Optimization Society. It currently consists of two series: A and B. The "A" series contains general publications. The "B" series focuses on topical...
(MP) of the classic format above is
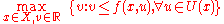
Constraints can be incorporated explicitly in these models. The generic constrained classic format is
The equivalent constrained MP format is
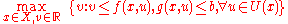
In another effort and in one of the non-probabilistic models, Erfani and Utyuzhnikov , use the fuzzy variables in order to quantify the uncertainties within the design parameters. They introduce a Robust measure in context of multiobjective optimization
Multiobjective optimization
Multi-objective optimization , also known as multi-criteria or multi-attribute optimization, is the process of simultaneously optimizing two or more conflicting objectives subject to certain constraints....
to find the robust Pareto optimal solutions.
Probabilistic robust optimization models
These models quantify the uncertainty in the "true" value of the parameter of interest by probability distribution functions. They have been traditionally classified as stochastic programmingStochastic programming
Stochastic programming is a framework for modeling optimization problems that involve uncertainty. Whereas deterministic optimization problems are formulated with known parameters, real world problems almost invariably include some unknown parameters. When the parameters are known only within...
and stochastic optimization
Stochastic optimization
Stochastic optimization methods are optimization methods that generate and use random variables. For stochastic problems, the random variables appear in the formulation of the optimization problem itself, which involve random objective functions or random constraints, for example. Stochastic...
models.
See also
- Stability radiusStability radiusThe stability radius of an object at a given nominal point is the radius of the largest ball, centered at the nominal point, all whose elements satisfy pre-determined stability conditions...
- MinimaxMinimaxMinimax is a decision rule used in decision theory, game theory, statistics and philosophy for minimizing the possible loss for a worst case scenario. Alternatively, it can be thought of as maximizing the minimum gain...
- Minimax estimator
- Minimax regret
- Robust statisticsRobust statisticsRobust statistics provides an alternative approach to classical statistical methods. The motivation is to produce estimators that are not unduly affected by small departures from model assumptions.- Introduction :...
- Robust decision makingRobust decision makingRobust decision making is an iterative decision analytic framework that helps identify potential robust strategies, characterize the vulnerabilities of such strategies, and evaluate the tradeoffs among them...
- Stochastic programmingStochastic programmingStochastic programming is a framework for modeling optimization problems that involve uncertainty. Whereas deterministic optimization problems are formulated with known parameters, real world problems almost invariably include some unknown parameters. When the parameters are known only within...
- Stochastic optimizationStochastic optimizationStochastic optimization methods are optimization methods that generate and use random variables. For stochastic problems, the random variables appear in the formulation of the optimization problem itself, which involve random objective functions or random constraints, for example. Stochastic...
- Info-gap decision theoryInfo-gap decision theoryInfo-gap decision theory is a non-probabilistic decision theory that seeks to optimize robustness to failure – or opportuneness for windfall – under severe uncertainty, in particular applying sensitivity analysis of the stability radius type to perturbations in the value of a given estimate of the...