
Maxima and minima
Encyclopedia
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the maximum and minimum (plural: maxima and minima) of a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
, known collectively as extrema (singular: extremum), are the largest and smallest value that the function takes at a point either within a given neighborhood (local or relative extremum) or on the function domain
Domain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
in its entirety (global or absolute extremum).
More generally, the maximum and minimum of a set (as defined in set theory
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
) are the greatest and least element
Greatest element
In mathematics, especially in order theory, the greatest element of a subset S of a partially ordered set is an element of S which is greater than or equal to any other element of S. The term least element is defined dually...
in the set. Unbounded infinite sets such as the set of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s have no minimum and maximum.
To locate extreme values is the basic objective of optimization.
Analytical definition
A real-valued functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
f defined on a real line
Real line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
is said to have a local (or relative) maximum point at the point x∗, if there exists some ε > 0 such that f(x∗) ≥ f(x) when |x − x∗| < ε. The value of the function at this point is called maximum of the function. Similarly, a function has a local minimum point at x∗, if f(x∗) ≤ f(x) when |x − x∗| < ε. The value of the function at this point is called minimum of the function.
A function has a global (or absolute) maximum point at x∗ if f(x∗) ≥ f(x) for all x. Similarly, a function has a global (or absolute) minimum point at x∗ if f(x∗) ≤ f(x) for all x. The global maximum and global minimum points are also known as the arg max and arg min: the argument (input) at which the maximum (respectively, minimum) occurs.
Restricted domains: There may be maxima and minima for a function whose
domain
Domain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
does not include all real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s. A real-valued function, whose domain is any set, can have a global maximum and minimum. There may also be local maxima and local minima points, but only at points of the domain set where the concept of neighborhood is defined. A neighborhood plays the role of the set of x such that
|x − x∗| < ε.
A continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
(real-valued) function on a compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
set always takes maximum and minimum values on that set. An important example is a function whose domain is a closed (and bounded) interval
Interval
Interval may refer to:* Interval , a range of numbers * Interval measurements or interval variables in statistics is a level of measurement...
of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s (see the graph above). The neighborhood requirement precludes a local maximum or minimum at an endpoint of an interval. However, an endpoint may still be a global maximum or minimum. Thus it is not always true, for finite domains, that a global maximum (minimum) must also be a local maximum (minimum).
Finding functional maxima and minima
Finding global maxima and minima is the goal of mathematical optimization. If a function is continuous on a closed interval, then by the extreme value theoremExtreme value theorem
In calculus, the extreme value theorem states that if a real-valued function f is continuous in the closed and bounded interval [a,b], then f must attain its maximum and minimum value, each at least once...
global maxima and minima exist. Furthermore, a global maximum (or minimum) either must be a local maximum (or minimum) in the interior of the domain, or must lie on the boundary of the domain. So a method of finding a global maximum (or minimum) is to look at all the local maxima (or minima) in the interior, and also look at the maxima (or minima) of the points on the boundary; and take the biggest (or smallest) one.
Local extrema can be found by Fermat's theorem
Fermat's theorem (stationary points)
In mathematics, Fermat's theorem is a method to find local maxima and minima of differentiable functions on open sets by showing that every local extremum of the function is a stationary point...
, which states that they must occur at critical point
Critical point (mathematics)
In calculus, a critical point of a function of a real variable is any value in the domain where either the function is not differentiable or its derivative is 0. The value of the function at a critical point is a critical value of the function...
s. One can distinguish whether a critical point is a local maximum or local minimum by using the
first derivative test
First derivative test
In calculus, the first derivative test uses the first derivative of a function to determine whether a given critical point of a function is a local maximum, a local minimum, or neither.-Intuitive explanation:...
or second derivative test
Second derivative test
In calculus, the second derivative test is a criterion often useful for determining whether a given stationary point of a function is a local maximum or a local minimum using the value of the second derivative at the point....
.
For any function that is defined piecewise
Piecewise
On mathematics, a piecewise-defined function is a function whose definition changes depending on the value of the independent variable...
, one finds a maxima (or minima) by finding the maximum (or minimum) of each piece separately; and then seeing which one is biggest (or smallest).
Examples
- The function x2 has a unique global minimum at x = 0.
- The function x3 has no global minima or maxima. Although the first derivative (3x2) is 0 at x = 0, this is an inflection pointInflection pointIn differential calculus, an inflection point, point of inflection, or inflection is a point on a curve at which the curvature or concavity changes sign. The curve changes from being concave upwards to concave downwards , or vice versa...
. - The function
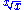 has a unique global maximum at x = eE (mathematical constant)The mathematical constant ' is the unique real number such that the value of the derivative of the function at the point is equal to 1. The function so defined is called the exponential function, and its inverse is the natural logarithm, or logarithm to base...
has a unique global maximum at x = eE (mathematical constant)The mathematical constant ' is the unique real number such that the value of the derivative of the function at the point is equal to 1. The function so defined is called the exponential function, and its inverse is the natural logarithm, or logarithm to base...
. (See figure at right) - The function x-x has a unique global maximum over the positive real numbers at x = 1/e.
- The function x3/3 − x has first derivative x2 − 1 and second derivativeSecond derivativeIn calculus, the second derivative of a function ƒ is the derivative of the derivative of ƒ. Roughly speaking, the second derivative measures how the rate of change of a quantity is itself changing; for example, the second derivative of the position of a vehicle with respect to time is...
2x. Setting the first derivative to 0 and solving for x gives stationary points at −1 and +1. From the sign of the second derivative we can see that −1 is a local maximum and +1 is a local minimum. Note that this function has no global maximum or minimum. - The function |x| has a global minimum at x = 0 that cannot be found by taking derivatives, because the derivative does not exist at x = 0.
- The function cos(x) has infinitely many global maxima at 0, ±2π, ±4π, …, and infinitely many global minima at ±π, ±3π, ….
- The function 2 cos(x) − x has infinitely many local maxima and minima, but no global maximum or minimum.
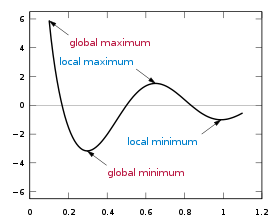
- The function cos(3πx)/x with 0.1 ≤ x ≤ 1.1 has a global maximum at x = 0.1 (a boundary), a global minimum near x = 0.3, a local maximum near x = 0.6, and a local minimum near x = 1.0. (See figure at top of page.)
- The function x3 + 3x2 − 2x + 1 defined over the closed interval (segment) [−4,2] has two extrema: one local maximum at x = −1−√15⁄3, one local minimum at x = −1+√15⁄3, a global maximum at x = 2 and a global minimum at x = −4.
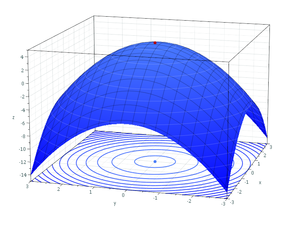
Functions of more than one variable
For functions of more than one variable, similar conditions apply. For example, in the (enlargeable) figure at the right, the necessary conditions for a local maximum are similar to those of a function with only one variable. The first partial derivatives as to z (the variable to be maximized) are zero at the maximum (the glowing dot on top in the figure). The second partial derivatives are negative. These are only necessary, not sufficient, conditions for a local maximum because of the possibility of a saddle pointSaddle point
In mathematics, a saddle point is a point in the domain of a function that is a stationary point but not a local extremum. The name derives from the fact that in two dimensions the surface resembles a saddle that curves up in one direction, and curves down in a different direction...
. For use of these conditions to solve for a maximum, the function z must also be differentiable throughout. The second partial derivative test
Second partial derivative test
In mathematics, the second partial derivative test is a method in multivariable calculus used to determine if a critical point of a function f is a minimum, maximum or saddle point.-Explanation:Suppose that...
can help classify the point as a relative maximum or relative minimum.
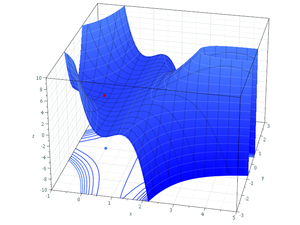
In contrast, there are substantial differences between functions of one variable and functions of more than one variable in the identification of global extrema. For example, if a bounded differentiable function f defined on a closed interval in the real line has a single critical point, which is a local minimum, then it is also a global minimum (use the intermediate value theorem
Intermediate value theorem
In mathematical analysis, the intermediate value theorem states that for each value between the least upper bound and greatest lower bound of the image of a continuous function there is at least one point in its domain that the function maps to that value....
and Rolle's theorem
Rolle's theorem
In calculus, Rolle's theorem essentially states that a differentiable function which attains equal values at two distinct points must have a point somewhere between them where the first derivative is zero.-Standard version of the theorem:If a real-valued function ƒ is continuous on a closed...
to prove this by reductio ad absurdum
Reductio ad absurdum
In logic, proof by contradiction is a form of proof that establishes the truth or validity of a proposition by showing that the proposition's being false would imply a contradiction...
). In two and more dimensions, this argument fails, as the function

shows. Its only critical point is at (0,0), which is a local minimum with ƒ(0,0) = 0. However, it cannot be a global one, because ƒ(4,1) = −11.
 |
 |
In relation to sets
Maxima and minima are more generally defined for sets. In general, if an ordered setOrdered set
In order theory in mathematics, a set with a binary relation R on its elements that is reflexive , antisymmetric and transitive is described as a partially ordered set or poset...
S has a greatest element
Greatest element
In mathematics, especially in order theory, the greatest element of a subset S of a partially ordered set is an element of S which is greater than or equal to any other element of S. The term least element is defined dually...
m, m is a maximal element
Maximal element
In mathematics, especially in order theory, a maximal element of a subset S of some partially ordered set is an element of S that is not smaller than any other element in S. The term minimal element is defined dually...
. Furthermore, if S is a subset of an ordered set T and m is the greatest element of S with respect to order induced by T, m is a least upper bound
Supremum
In mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
of S in T. The similar result holds for least element, minimal element and greatest lower bound
Infimum
In mathematics, the infimum of a subset S of some partially ordered set T is the greatest element of T that is less than or equal to all elements of S. Consequently the term greatest lower bound is also commonly used...
.
In the case of a general partial order, the least element (smaller than all other) should not be confused with a minimal element (nothing is smaller). Likewise, a greatest element
Greatest element
In mathematics, especially in order theory, the greatest element of a subset S of a partially ordered set is an element of S which is greater than or equal to any other element of S. The term least element is defined dually...
of a partially ordered set
Partially ordered set
In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
(poset) is an upper bound
Upper bound
In mathematics, especially in order theory, an upper bound of a subset S of some partially ordered set is an element of P which is greater than or equal to every element of S. The term lower bound is defined dually as an element of P which is lesser than or equal to every element of S...
of the set which is contained within the set, whereas a maximal element m of a poset A is an element of A such that if m ≤ b (for any b in A) then m = b. Any least element or greatest element of a poset is unique, but a poset can have several minimal or maximal elements. If a poset has more than one maximal element, then these elements will not be mutually comparable.
In a totally ordered
Total order
In set theory, a total order, linear order, simple order, or ordering is a binary relation on some set X. The relation is transitive, antisymmetric, and total...
set, or chain, all elements are mutually comparable, so such a set can have at most one minimal element and at most one maximal element. Then, due to mutual comparability, the minimal element will also be the least element and the maximal element will also be the greatest element. Thus in a totally ordered set we can simply use the terms minimum and maximum. If a chain is finite then it will always have a maximum and a minimum. If a chain is infinite then it need not have a maximum or a minimum. For example, the set of natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s has no maximum, though it has a minimum. If an infinite chain S is bounded, then the closure Cl(S) of the set occasionally has a minimum and a maximum, in such case they are called the greatest lower bound and the least upper bound of the set S, respectively..
See also
- First derivative testFirst derivative testIn calculus, the first derivative test uses the first derivative of a function to determine whether a given critical point of a function is a local maximum, a local minimum, or neither.-Intuitive explanation:...
- Second derivative testSecond derivative testIn calculus, the second derivative test is a criterion often useful for determining whether a given stationary point of a function is a local maximum or a local minimum using the value of the second derivative at the point....
- Limit superior and limit inferiorLimit superior and limit inferiorIn mathematics, the limit inferior and limit superior of a sequence can be thought of as limiting bounds on the sequence...
- Mechanical equilibriumMechanical equilibriumA standard definition of static equilibrium is:This is a strict definition, and often the term "static equilibrium" is used in a more relaxed manner interchangeably with "mechanical equilibrium", as defined next....
- Sample maximum and minimumSample maximum and minimumIn statistics, the maximum and sample minimum, also called the largest observation, and smallest observation, are the values of the greatest and least elements of a sample....
- Saddle pointSaddle pointIn mathematics, a saddle point is a point in the domain of a function that is a stationary point but not a local extremum. The name derives from the fact that in two dimensions the surface resembles a saddle that curves up in one direction, and curves down in a different direction...
External links
- Maxima and Minima From MathWorld--A Wolfram Web Resource.
- Thomas Simpson's work on Maxima and Minima at Convergence
- Application of Maxima and Minima with sub pages of solved problems

