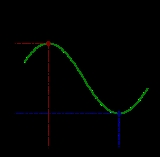
Extreme value theorem - AbsoluteAstronomy.com

Calculus

Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...

, the extreme value theorem states that if a real-valued function

Function (mathematics)

In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...

f is continuous

Continuous function

In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...

in the closed

Closed set

In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...

and bounded interval [a,b], then f must attain its maximum and minimum value, each at least once. That is, there exist numbers c and d in [a,b] such that:

A related theorem is the boundedness theorem which states that a continuous function f in the closed interval [a,b] is bounded

Bounded function

In mathematics, a function f defined on some set X with real or complex values is called bounded, if the set of its values is bounded. In other words, there exists a real number M...

on that interval. That is, there exist real numbers m and M such that:

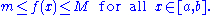
The extreme value theorem enriches the boundedness theorem by saying that not only is the function bounded, but it also attains its least upper bound as its maximum and its greatest lower bound as its minimum.

The extreme value theorem is used to prove Rolle's theorem

Rolle's theorem

In calculus, Rolle's theorem essentially states that a differentiable function which attains equal values at two distinct points must have a point somewhere between them where the first derivative is zero.-Standard version of the theorem:If a real-valued function ƒ is continuous on a closed...

. In a formulation due to Karl Weierstrass

Karl Weierstrass

Karl Theodor Wilhelm Weierstrass was a German mathematician who is often cited as the "father of modern analysis".- Biography :Weierstrass was born in Ostenfelde, part of Ennigerloh, Province of Westphalia....

, this theorem states that a continuous function from a compact space

Compact space

In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...

to a subset of the real number

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

s attains its maximum and minimum.

History

The extreme value theorem was originally proved by Bolzano in 1830's in a work Function Theory but the work remained unpublished until 1930. Bolzano's proof consisted of showing that a continuous function on a closed interval was bounded, and then showing that the function attained its maximum and minimum value. Both proofs involved what is known today as the Bolzano–Weierstrass theorem . The result was also discovered later by Weierstrass in 1860.

Functions to which theorem does not apply

The following examples show why the function domain must be closed and bounded in order for the theorem to apply. Each fails to attain a maximum on the given interval.

ƒ(x) = x defined over [0, ∞) is not bounded from above.
ƒ(x) = defined over [0, ∞) is bounded but does not attain its least upper bound 1.
ƒ(x) = defined over (0, 1] is not bounded from above.
ƒ(x) = 1 – x defined over (0, 1] is bounded but never attains its least upper bound 1.

Defining ƒ(0) = 0 in the last two examples shows that both theorems require continuity on [a, b].

Extension to semi-continuous functions

If the continuity of the function f is weakened to semi-continuity

Semi-continuity

In mathematical analysis, semi-continuity is a property of extended real-valued functions that is weaker than continuity...

, then the corresponding half of the boundedness theorem and the extreme value theorem hold and the values –∞ or +∞, respectively, from the extended real number line

Extended real number line

In mathematics, the affinely extended real number system is obtained from the real number system R by adding two elements: +∞ and −∞ . The projective extended real number system adds a single object, ∞ and makes no distinction between "positive" or "negative" infinity...

can be allowed as possible values. More precisely:

Theorem: If a function f : [a,b] → [–∞,∞) is upper semi-continuous, meaning that

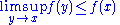
for all x in [a,b], then f is bounded above and attains its supremum.

Proof: If f(x) = –∞ for all x in [a,b], then the supremum is also –∞ and the theorem is true. In all other cases, the proof is a slight modification of the proofs given above. In the proof of the boundedness theorem, the upper semi-continuity of f at x only implies that the limit superior of the subsequence {f(x_{n_k})} is bounded above by f(x) < ∞, but that is enough to obtain the contradiction. In the proof of the extreme value theorem, upper semi-continuity of f at d implies that the limit superior of the subsequence {f(d_{n_k})} is bounded above by f(d), but this suffices to conclude that f(d) = M. ∎

Q.E.D.

Q.E.D. is an initialism of the Latin phrase , which translates as "which was to be demonstrated". The phrase is traditionally placed in its abbreviated form at the end of a mathematical proof or philosophical argument when what was specified in the enunciation — and in the setting-out —...

Applying this result to −f proves:

Theorem: If a function f : [a,b] → (–∞,∞] is lower semi-continuous, meaning that

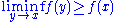
for all x in [a,b], then f is bounded below and attains its infimum

Infimum

In mathematics, the infimum of a subset S of some partially ordered set T is the greatest element of T that is less than or equal to all elements of S. Consequently the term greatest lower bound is also commonly used...

.

A real-valued function is upper as well as lower semi-continuous, if and only if it is continuous in the usual sense. Hence these two theorems imply the boundedness theorem and the extreme value theorem.

Topological formulation

In general topology

General topology

In mathematics, general topology or point-set topology is the branch of topology which studies properties of topological spaces and structures defined on them...

, the extreme value theorem follows from the general fact that compactness is preserved by continuous function

Continuous function

s, and the fact that a subset of the real line is compact if and only if it is both closed and bounded.

Proving the theorems

We look at the proof for the upper bound

Upper bound

In mathematics, especially in order theory, an upper bound of a subset S of some partially ordered set is an element of P which is greater than or equal to every element of S. The term lower bound is defined dually as an element of P which is lesser than or equal to every element of S...

and the maximum of f. By applying these results to the function –f, the existence of the lower bound and the result for the minimum of f follows. Also note that everything in the proof is done within the context of the real numbers.

We first prove the boundedness theorem, which is a step in the proof of the extreme value theorem. The basic steps involved in the proof of the extreme value theorem are:

Prove the boundedness theorem.
Find a sequence so that its image
Image (mathematics)
In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...

converges to the supremum
Supremum
In mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...

of f.
Show that there exists a subsequence
Subsequence
In mathematics, a subsequence is a sequence that can be derived from another sequence by deleting some elements without changing the order of the remaining elements...

that converges to a point in the domain
Domain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...

.
Use continuity to show that the image of the subsequence converges to the supremum.

Proof of the boundedness theorem

Suppose the function f is not bounded above on the interval [a,b]. Then, by the Archimedean property

Archimedean property

In abstract algebra and analysis, the Archimedean property, named after the ancient Greek mathematician Archimedes of Syracuse, is a property held by some ordered or normed groups, fields, and other algebraic structures. Roughly speaking, it is the property of having no infinitely large or...

of the real numbers, for every natural number n, there exists an x_n in [a,b] such that f(x_n) > n. This defines a sequence

Sequence

In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...

{x_n}. Because [a,b] is bounded, the Bolzano-Weierstrass theorem implies that there exists a convergent subsequence {

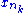} of {x_n}. Denote its limit by x. As [a,b] is closed, it contains x. Because f is continuous at x, we know that {f(

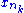)} converges to the real number f(x) (as f is sequentially continuous at x.) But f(x_{n_k}) > n_k ≥ k for every k, which implies that {f(x_{n_k})} diverges to +∞

Extended real number line

, a contradiction. Therefore, f is bounded above on [a,b]. ∎

Q.E.D.

Proof of the extreme value theorem

By the boundedness theorem, f is bounded from above, hence, by the Dedekind-completeness of the real numbers, the least upper bound (supremum) M of f exists. It is necessary to find a d in [a,b] such that M = f(d). Let n be a natural number. As M is the least upper bound, M – 1/n is not an upper bound for f. Therefore, there exists d_n in [a,b] so that M – 1/n < f(d_n). This defines a sequence {d_n}. Since M is an upper bound for f, we have M – 1/n < f(d_n) ≤ M for all n. Therefore, the sequence {f(d_n)} converges to M.

The Bolzano-Weierstrass theorem tells us that there exists a subsequence {

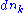}, which converges to some d and, as [a,b] is closed, d is in [a,b]. Since f is continuous at d, the sequence {f(

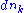)} converges to f(d). But {f(d_{n_k})} is a subsequence of {f(d_n)} that converges to M, so M = f(d). Therefore, f attains its supremum M at d. ∎

Q.E.D.

Alternative proof of the extreme value theorem

The set } is a bounded set. Hence, its least upper bound exists by least upper bound property of the real numbers. Let M = sup(f(x)) on [a, b]. If there is no point x on [a, b] so that f(x) = M then
f(x) < M on [a, b]. Therefore 1/(M − f(x)) is continuous on [a, b].

However, to every positive number ε, there is always some x in [a, b] such that M − f(x) < ε because M is the least upper bound. Hence,
1/(M − f(x)) > 1/ε, which means that 1/(M − f(x)) is not bounded. Since every continuous function on a [a, b] is bounded, this contradicts the conclusion that 1/(M − f(x)) was continuous on [a, b]. Therefore there must be a point x in [a, b] such that f(x) = M. ∎

Q.E.D.

Proof using the hyperreals

In the setting of non-standard calculus

Non-standard calculus

In mathematics, non-standard calculus is the modern application of infinitesimals, in the sense of non-standard analysis, to differential and integral calculus...

, let N be an infinite hyperinteger

Hyperinteger

In non-standard analysis, a hyperinteger N is a hyperreal number equal to its own integer part. A hyperinteger may be either finite or infinite. A finite hyperinteger is an ordinary integer...

. The interval [0, 1] has a natural hyperreal extension. Consider its partition into N subintervals of equal infinitesimal

Infinitesimal

Infinitesimals have been used to express the idea of objects so small that there is no way to see them or to measure them. The word infinitesimal comes from a 17th century Modern Latin coinage infinitesimus, which originally referred to the "infinite-th" item in a series.In common speech, an...

length 1/N, with partition points x_i = i /N as i "runs" from 0 to N. The function ƒ is also naturally extended to a function ƒ* defined on the hyperreals between 0 and 1. Note that in the standard setting (when N is finite), a point with the maximal value of ƒ can always be chosen among the N+1 points x_i, by induction. Hence, by the transfer principle

Transfer principle

In model theory, a transfer principle states that all statements of some language that are true for some structure are true for another structure...

, there is a hyperinteger i₀ such that 0 ≤ i₀ ≤ N and

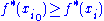for all i = 0, …, N. Consider the real point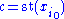

where st is the standard part function

Standard part function

In non-standard analysis, the standard part function is a function from the limited hyperreals to the reals, which associates to every hyperreal, the unique real infinitely close to it. As such, it is a mathematical implementation of the historical concept of adequality introduced by Pierre de...

. An arbitrary real point x lies in a suitable sub-interval of the partition, namely

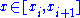, so that st(x_i) = x. Applying st to the inequality

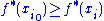, we obtain

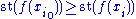. By continuity of ƒ we have

.
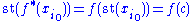Hence ƒ(c) ≥ ƒ(x), for all x, proving c to be a maximum of ƒ. See .

External links

A Proof for extreme value theorem at cut-the-knot
Cut-the-knot
Cut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
Extreme Value Theorem by Jacqueline Wandzura with additional contributions by Stephen Wandzura, the Wolfram Demonstrations Project
Wolfram Demonstrations Project
The Wolfram Demonstrations Project is hosted by Wolfram Research, whose stated goal is to bring computational exploration to the widest possible audience. It consists of an organized, open-source collection of small interactive programs called Demonstrations, which are meant to visually and...

.

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.