
Quadratic programming
Encyclopedia
Quadratic programming is a special type of mathematical optimization problem
. It is the problem of optimizing (minimizing or maximizing) a quadratic function of several variables subject to linear constraints on these variables.
The quadratic programming problem can be formulated as:
Assume x belongs to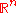 space. Both x and c are column vectors with n elements (n×1 matrices), and Q is a symmetric n×n matrix.
space. Both x and c are column vectors with n elements (n×1 matrices), and Q is a symmetric n×n matrix.
Minimize (with respect to x)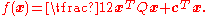
Subject to one or more constraints of the form: (inequality constraint)
(inequality constraint)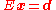 (equality constraint)
(equality constraint)
where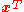 indicates the vector transpose
indicates the vector transpose
of . The notation
. The notation  means that every entry of the vector
means that every entry of the vector 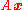 is less than or equal to the corresponding entry of the vector
is less than or equal to the corresponding entry of the vector  .
.
If the matrix is positive semidefinite matrix
is positive semidefinite matrix
, then is a convex function
is a convex function
: In this case the quadratic program has a global minimizer if there exists some feasible vector (satisfying the constraints) and if
(satisfying the constraints) and if  is bounded below on the feasible region. If the matrix
is bounded below on the feasible region. If the matrix  is positive definite
is positive definite
and the problem has a feasible solution, then the global minimizer is unique.
If is zero, then the problem becomes a linear program
is zero, then the problem becomes a linear program
.
A related programming problem, quadratically constrained quadratic programming
, can be posed by adding quadratic constraints on the variables.
and seeking the extremum of the Lagrangian, it may be readily shown that the solution to the equality constrained problem is given by the linear system:

where is a set of Lagrange multipliers which come out of the solution alongside
is a set of Lagrange multipliers which come out of the solution alongside  . For inequality constrained problems a variety of methods are commonly used, including
. For inequality constrained problems a variety of methods are commonly used, including
Convex quadratic programming is a special case of the more general field of convex optimization.
of a QP is also a QP. To see that let us focus on the case where and Q is positive definite. We write the Lagrangian
and Q is positive definite. We write the Lagrangian
function as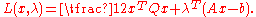
Defining the (Lagrangian) dual function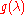 , defined as
, defined as 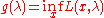 , we find an infimum
, we find an infimum
of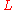 , using
, using 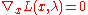 :
:
 , hence the dual function is
, hence the dual function is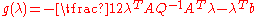
hence the Lagrangian dual of the QP is
maximize: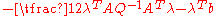
subject to: .
.
Besides the Lagrangian duality theory, there are other duality pairings (e.g. Wolfe, etc.).
Q, the ellipsoid method
solves the problem in polynomial time. If, on the other hand, Q is indefinite, then the problem is NP-hard
. In fact, even if Q has only one negative eigenvalue, the problem is NP-hard
.
licenses:
Free open-source copyleft (reciprocal)
licenses:
Other Free open-source licenses:
Proprietary:
Optimization problem
In mathematics and computer science, an optimization problem is the problem of finding the best solution from all feasible solutions. Optimization problems can be divided into two categories depending on whether the variables are continuous or discrete. An optimization problem with discrete...
. It is the problem of optimizing (minimizing or maximizing) a quadratic function of several variables subject to linear constraints on these variables.
The quadratic programming problem can be formulated as:
Assume x belongs to
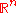 space. Both x and c are column vectors with n elements (n×1 matrices), and Q is a symmetric n×n matrix.
space. Both x and c are column vectors with n elements (n×1 matrices), and Q is a symmetric n×n matrix.Minimize (with respect to x)
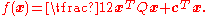
Subject to one or more constraints of the form:
 (inequality constraint)
(inequality constraint)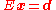 (equality constraint)
(equality constraint)where
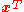 indicates the vector transpose
indicates the vector transposeTranspose
In linear algebra, the transpose of a matrix A is another matrix AT created by any one of the following equivalent actions:...
of
 . The notation
. The notation  means that every entry of the vector
means that every entry of the vector 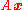 is less than or equal to the corresponding entry of the vector
is less than or equal to the corresponding entry of the vector  .
.If the matrix
 is positive semidefinite matrix
is positive semidefinite matrixPositive-definite matrix
In linear algebra, a positive-definite matrix is a matrix that in many ways is analogous to a positive real number. The notion is closely related to a positive-definite symmetric bilinear form ....
, then
 is a convex function
is a convex functionConvex function
In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
: In this case the quadratic program has a global minimizer if there exists some feasible vector
 (satisfying the constraints) and if
(satisfying the constraints) and if  is bounded below on the feasible region. If the matrix
is bounded below on the feasible region. If the matrix  is positive definite
is positive definitePositive-definite matrix
In linear algebra, a positive-definite matrix is a matrix that in many ways is analogous to a positive real number. The notion is closely related to a positive-definite symmetric bilinear form ....
and the problem has a feasible solution, then the global minimizer is unique.
If
 is zero, then the problem becomes a linear program
is zero, then the problem becomes a linear programLinear programming
Linear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...
.
A related programming problem, quadratically constrained quadratic programming
Quadratically constrained quadratic program
In mathematics, a quadratically constrained quadratic program is an optimization problem in which both the objective function and the constraints are quadratic functions...
, can be posed by adding quadratic constraints on the variables.
Solution methods
If there are only equality constraints, the quadratic programming problem may be approached relatively easily. By using Lagrange multipliersLagrange multipliers
In mathematical optimization, the method of Lagrange multipliers provides a strategy for finding the maxima and minima of a function subject to constraints.For instance , consider the optimization problem...
and seeking the extremum of the Lagrangian, it may be readily shown that the solution to the equality constrained problem is given by the linear system:

where
 is a set of Lagrange multipliers which come out of the solution alongside
is a set of Lagrange multipliers which come out of the solution alongside  . For inequality constrained problems a variety of methods are commonly used, including
. For inequality constrained problems a variety of methods are commonly used, including- interior pointInterior point methodInterior point methods are a certain class of algorithms to solve linear and nonlinear convex optimization problems.The interior point method was invented by John von Neumann...
, - active set,
- augmented LagrangianAugmented Lagrangian methodAugmented Lagrangian methods are a certain class of algorithms for solving constrained optimization problems. They have similarities to penalty methods in that they replace a constrained optimization problem by a series of unconstrained problems; the difference is that the augmented Lagrangian...
, - conjugate gradientConjugate gradient methodIn mathematics, the conjugate gradient method is an algorithm for the numerical solution of particular systems of linear equations, namely those whose matrix is symmetric and positive-definite. The conjugate gradient method is an iterative method, so it can be applied to sparse systems that are too...
, - gradient projection,
- extensions of the simplex algorithmSimplex algorithmIn mathematical optimization, Dantzig's simplex algorithm is a popular algorithm for linear programming. The journal Computing in Science and Engineering listed it as one of the top 10 algorithms of the twentieth century....
.
Convex quadratic programming is a special case of the more general field of convex optimization.
Lagrangian duality
The Lagrangian dualDual problem
In constrained optimization, it is often possible to convert the primal problem to a dual form, which is termed a dual problem. Usually dual problem refers to the Lagrangian dual problem but other dual problems are used, for example, the Wolfe dual problem and the Fenchel dual problem...
of a QP is also a QP. To see that let us focus on the case where
 and Q is positive definite. We write the Lagrangian
and Q is positive definite. We write the LagrangianLagrange multipliers
In mathematical optimization, the method of Lagrange multipliers provides a strategy for finding the maxima and minima of a function subject to constraints.For instance , consider the optimization problem...
function as
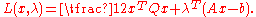
Defining the (Lagrangian) dual function
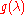 , defined as
, defined as 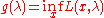 , we find an infimum
, we find an infimumInfimum
In mathematics, the infimum of a subset S of some partially ordered set T is the greatest element of T that is less than or equal to all elements of S. Consequently the term greatest lower bound is also commonly used...
of
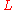 , using
, using 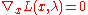 :
: , hence the dual function is
, hence the dual function is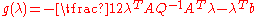
hence the Lagrangian dual of the QP is
maximize:
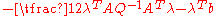
subject to:
 .
.Besides the Lagrangian duality theory, there are other duality pairings (e.g. Wolfe, etc.).
Complexity
For positive definitePositive-definite matrix
In linear algebra, a positive-definite matrix is a matrix that in many ways is analogous to a positive real number. The notion is closely related to a positive-definite symmetric bilinear form ....
Q, the ellipsoid method
Ellipsoid method
In mathematical optimization, the ellipsoid method is an iterative method for minimizing convex functions. When specialized to solving feasible linear optimization problems with rational data, the ellipsoid method is an algorithm, which finds an optimal solution in a finite number of steps.The...
solves the problem in polynomial time. If, on the other hand, Q is indefinite, then the problem is NP-hard
NP-hard
NP-hard , in computational complexity theory, is a class of problems that are, informally, "at least as hard as the hardest problems in NP". A problem H is NP-hard if and only if there is an NP-complete problem L that is polynomial time Turing-reducible to H...
. In fact, even if Q has only one negative eigenvalue, the problem is NP-hard
NP-hard
NP-hard , in computational complexity theory, is a class of problems that are, informally, "at least as hard as the hardest problems in NP". A problem H is NP-hard if and only if there is an NP-complete problem L that is polynomial time Turing-reducible to H...
.
Solvers and scripting (programming) languages
Free open-source permissivePermissive free software licence
A permissive free software licence is a class of free software licence with minimal requirements about how the software can be redistributed. This is in contrast to copyleft licences, which have reciprocity / share-alike requirements. Both sets of free software licences offer the same freedoms in...
licenses:
| Name | License | Brief info |
|---|---|---|
| OpenOpt OpenOpt OpenOpt is an open-source framework for numerical optimization, nonlinear equations and systems of them. It is licensed under the BSD license, making it available to be used in both open- and closed-code software. The package already has some essential .... |
BSD BSD licenses BSD licenses are a family of permissive free software licenses. The original license was used for the Berkeley Software Distribution , a Unix-like operating system after which it is named.... |
Universal cross-platform numerical optimization framework, see its QP page and other problems involved. Uses NumPy arrays and SciPy SciPy SciPy is an open source library of algorithms and mathematical tools for the Python programming language.SciPy contains modules for optimization, linear algebra, integration, interpolation, special functions, FFT, signal and image processing, ODE solvers and other tasks common in science and... sparse matrices. |
| qp-numpy | BSD BSD licenses BSD licenses are a family of permissive free software licenses. The original license was used for the Berkeley Software Distribution , a Unix-like operating system after which it is named.... |
Built around the qld code written by K.Schittkowski of the University of Bayreuth, Germany |
Free open-source copyleft (reciprocal)
Copyleft
Copyleft is a play on the word copyright to describe the practice of using copyright law to offer the right to distribute copies and modified versions of a work and requiring that the same rights be preserved in modified versions of the work...
licenses:
| Name | License | Brief info |
|---|---|---|
| CVXOPT | GPL | General purpose convex optimization solver written in Python OOQP |
| Octave | GPL | General purpose GNU Octave GNU Octave GNU Octave is a high-level language, primarily intended for numerical computations. It provides a convenient command-line interface for solving linear and nonlinear problems numerically, and for performing other numerical experiments using a language that is mostly compatible with MATLAB... solver for Quadratic Programming problems |
Other Free open-source licenses:
| Name | License | Brief info |
|---|---|---|
| CGAL | QPL | An exact solver QP_solver, part of the Computational Geometry Algorithms Library (CGAL) |
Proprietary:
Proprietary software
Proprietary software is computer software licensed under exclusive legal right of the copyright holder. The licensee is given the right to use the software under certain conditions, while restricted from other uses, such as modification, further distribution, or reverse engineering.Complementary...
| Name | Brief info |
|---|---|
| AIMMS AIMMS AIMMS is a software system designed for modeling and solving large-scale optimization and scheduling-type problems.... |
|
| AMPL AMPL AMPL, an acronym for "A Mathematical Programming Language", is an algebraic modeling language for describing and solving high-complexity problems for large-scale mathematical computation AMPL, an acronym for "A Mathematical Programming Language", is an algebraic modeling language for describing and... |
|
| CPLEX CPLEX IBM ILOG CPLEX Optimization Studio is an optimization software package. In 2004, the work on CPLEX earned the first .... |
Popular solver with an API for several programming languages |
| EXCEL Excel Excel may refer to:* Microsoft Excel, a spreadsheet application by Microsoft Corporation* Excel , a brand of chewing gum produced by Wrigley's* Excel , a crossover thrash/punk band from Venice, California... Solver Function |
|
| FinMath | A .NET .NET Framework The .NET Framework is a software framework that runs primarily on Microsoft Windows. It includes a large library and supports several programming languages which allows language interoperability... numerical library containing an interior-point primal-dual Interior point method Interior point methods are a certain class of algorithms to solve linear and nonlinear convex optimization problems.The interior point method was invented by John von Neumann... solver for convex quadratic programming problems. |
| GAMS General Algebraic Modeling System The General Algebraic Modeling System is a high-level modeling system for mathematical optimization. GAMS is designed for modeling and solving linear, nonlinear, and mixed-integer optimization problems. The system is tailored for complex, large-scale modeling applications and allows the user to... |
|
| Gurobi Gurobi Gurobi is a commercial software package for solving large-scale linear optimization, quadratic optimization, and mixed-integer optimization problems... |
Solver with parallel algorithms for large-scale linear programs, quadratic programs and mixed-integer programs. Free for academic use. |
| Lingo | |
| MATLAB MATLAB MATLAB is a numerical computing environment and fourth-generation programming language. Developed by MathWorks, MATLAB allows matrix manipulations, plotting of functions and data, implementation of algorithms, creation of user interfaces, and interfacing with programs written in other languages,... |
A general-purpose and matrix-oriented programming-language for numerical computing. Quadratic programming in MATLAB requires the Optimization Toolbox in addition to the base MATLAB product |
| Mathematica Mathematica Mathematica is a computational software program used in scientific, engineering, and mathematical fields and other areas of technical computing... |
A general-purpose programming-language for mathematics, including symbolic and numerical capabilities. |
| MOSEK MOSEK MOSEK is a software package for the solution of linear, mixed-integer linear, quadratic, mixed-integer quadratic, quadratically constraint, conic and convex nonlinear mathematical optimization problems. The emphasize in MOSEK is on solving large scale sparse problems. Particularly the... |
A solver for large scale optimization with API for several languages (C++,java,.net, Matlab and python) |
| OptimJ OptimJ OptimJ is an extension of the Java with language support for writing optimization models and abstractions for bulk data processing. OptimJ aims at providing a clear and concise algebraic notation for optimization modeling, removing compatibility barriers between optimization modeling and... |
Free Java-based Modeling Language for Optimization supporting multiple target solvers and available as an Eclipse plugin. |
| Solver Foundation | A .NET .NET Framework The .NET Framework is a software framework that runs primarily on Microsoft Windows. It includes a large library and supports several programming languages which allows language interoperability... platform for modeling, scheduling, and optimization |
| TOMLAB TOMLAB The TOMLAB Optimization Environment is a modeling platform for solving applied optimization problems in MATLAB.-Description:TOMLAB is a general purpose development and modeling environment in MATLAB for research, teaching and practical solution of optimization problems... |
Supports global optimization, integer programming, all types of least sqaures, linear, quadratic and unconstrained programming for MATLAB MATLAB MATLAB is a numerical computing environment and fourth-generation programming language. Developed by MathWorks, MATLAB allows matrix manipulations, plotting of functions and data, implementation of algorithms, creation of user interfaces, and interfacing with programs written in other languages,... . TOMLAB supports solvers like Gurobi Gurobi Gurobi is a commercial software package for solving large-scale linear optimization, quadratic optimization, and mixed-integer optimization problems... , CPLEX CPLEX IBM ILOG CPLEX Optimization Studio is an optimization software package. In 2004, the work on CPLEX earned the first .... , SNOPT SNOPT SNOPT is a software package for solving large-scale optimization problems written by Philip Gill, Walter Murray and Michael Saunders.... and KNITRO KNITRO KNITRO is a software package for solving large scale mathematical optimization problems. KNITRO is specialized for nonlinear optimization, but also solves linear programming problems, quadratic programming problems, and systems of nonlinear equations. The unknowns in these problems must be... . |
| Xpress |
See also
- Support vector machineSupport vector machineA support vector machine is a concept in statistics and computer science for a set of related supervised learning methods that analyze data and recognize patterns, used for classification and regression analysis...
- Sequential quadratic programmingSequential quadratic programmingSequential quadratic programming is an iterative method for nonlinear optimization. SQP methods are used on problems for which the objective function and the constraints are twice continuously differentiable....
- Quadratically constrained quadratic programmingQuadratically constrained quadratic programIn mathematics, a quadratically constrained quadratic program is an optimization problem in which both the objective function and the constraints are quadratic functions...

