
Linear-fractional programming
Encyclopedia
In mathematical optimization, linear-fractional programming (LFP) is a generalization of linear programming
(LP). Whereas the objective function in linear programs are linear functions
, the objective function in a linear-fractional program is a ratio of two linear functions. A linear program can be regarded as a special case of a linear-fractional program in which the denominator is the constant function one.
,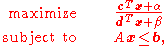
where represents the vector of variables to be determined,
represents the vector of variables to be determined, 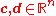 and
and  are vectors of (known) coefficients,
are vectors of (known) coefficients, 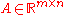 is a (known) matrix of coefficients and
is a (known) matrix of coefficients and 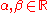 are constants. The domain of the objective function is defined by
are constants. The domain of the objective function is defined by 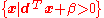 , i.e. where the denominator is positive.
, i.e. where the denominator is positive.
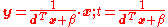 , the linear-fractional program above can be transformed to the equivalent linear program
, the linear-fractional program above can be transformed to the equivalent linear program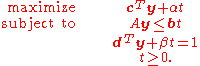
 and
and 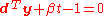 be denoted by
be denoted by  and
and 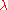 , respectively. Then the dual of the LFP above is
, respectively. Then the dual of the LFP above is 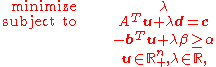
which is an LP and which coincides with the dual of the equivalent linear program resulting from the Charnes-Cooper transformation.
(hence quasilinear) with a monotone property, pseudoconvexity
, which is a stronger property than quasiconvexity
. A linear-fractional objective function is both pseudoconvex and pseudoconcave, hence pseudolinear. Since an LFP can be transformed to an LP, it can be solved using any LP solution method, such as the simplex algorithm
(of George B. Dantzig), the criss-cross algorithm
, or interior-point methods.
Linear programming
Linear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...
(LP). Whereas the objective function in linear programs are linear functions
Linear functional
In linear algebra, a linear functional or linear form is a linear map from a vector space to its field of scalars. In Rn, if vectors are represented as column vectors, then linear functionals are represented as row vectors, and their action on vectors is given by the dot product, or the...
, the objective function in a linear-fractional program is a ratio of two linear functions. A linear program can be regarded as a special case of a linear-fractional program in which the denominator is the constant function one.
Relation to linear programming
Both linear programming and linear-fractional programming represent optimization problems using linear equations and linear inequalities, which for each problem-instance define a feasible set. Fractional linear programs have a richer set of objective functions. Informally, linear programming computes a policy delivering the best outcome, such as maximum profit or lowest cost. In contrast, a linear-fractional programming is used to achieve the highest ratio of outcome to cost, the ratio representing the highest efficiency. For example, in the context of LP we maximize the objective function profit = income − cost and might obtain maximal profit of $100 (= $1100 of income − $1000 of cost). Thus, in LP we have an efficiency of $100/$1000 = 0.1. Using LFP we might obtain an efficiency of $10/$50 = 0.2 with a profit of only $10, which requires only $50 of investment however.Definition
Formally, a linear-fractional program is defined as the problem of maximizing (or minimizing) a ratio of affine functions over a polyhedronPolyhedron
In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
,
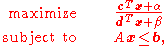
where
 represents the vector of variables to be determined,
represents the vector of variables to be determined, 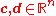 and
and  are vectors of (known) coefficients,
are vectors of (known) coefficients, 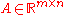 is a (known) matrix of coefficients and
is a (known) matrix of coefficients and 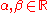 are constants. The domain of the objective function is defined by
are constants. The domain of the objective function is defined by 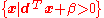 , i.e. where the denominator is positive.
, i.e. where the denominator is positive.Transformation to a linear program
Using the Charnes-Cooper transformation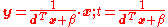 , the linear-fractional program above can be transformed to the equivalent linear program
, the linear-fractional program above can be transformed to the equivalent linear program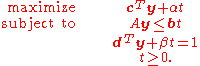
Duality
Let the dual variables associated with the constraints and
and 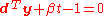 be denoted by
be denoted by  and
and 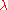 , respectively. Then the dual of the LFP above is
, respectively. Then the dual of the LFP above is 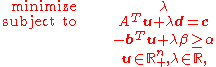
which is an LP and which coincides with the dual of the equivalent linear program resulting from the Charnes-Cooper transformation.
Properties of and algorithms for linear-fractional programs
The objective function in a linear-fractional problem is both quasiconcave and quasiconvexQuasiconvex function
In mathematics, a quasiconvex function is a real-valued function defined on an interval or on a convex subset of a real vector space such that the inverse image of any set of the form is a convex set...
(hence quasilinear) with a monotone property, pseudoconvexity
Pseudoconvex function
In convex analysis and the calculus of variations, branches of mathematics, a pseudoconvex function is a function that behaves like a convex function with respect to finding its local minima, but need not actually be convex...
, which is a stronger property than quasiconvexity
Quasiconvex function
In mathematics, a quasiconvex function is a real-valued function defined on an interval or on a convex subset of a real vector space such that the inverse image of any set of the form is a convex set...
. A linear-fractional objective function is both pseudoconvex and pseudoconcave, hence pseudolinear. Since an LFP can be transformed to an LP, it can be solved using any LP solution method, such as the simplex algorithm
Simplex algorithm
In mathematical optimization, Dantzig's simplex algorithm is a popular algorithm for linear programming. The journal Computing in Science and Engineering listed it as one of the top 10 algorithms of the twentieth century....
(of George B. Dantzig), the criss-cross algorithm
Criss-cross algorithm
In mathematical optimization, the criss-cross algorithm denotes a family of algorithms for linear programming. Variants of the criss-cross algorithm also solve more general problems with linear inequality constraints and nonlinear objective functions; there are criss-cross algorithms for...
, or interior-point methods.
Software
- WinGULF – educational interactive linear and linear-fractional programming solver with a lot of special options (pivoting, pricing, branching variables etc.).

