
Parameter
Encyclopedia
Parameter from Ancient Greek παρά also “para” meaning “beside, subsidiary” and μέτρον also “metron” meaning “measure”, can be interpreted in mathematics
, logic
, linguistics
, environmental science
and other disciplines.
In its common meaning, the term is used to identify a characteristic, a feature, a measurable factor that can help in defining a particular system. It is an important element to take into consideration for the evaluation or for the comprehension of an event, a project or any situation.
, statistics
, and the mathematical science
s, a parameter (from Ancient Greek παρά “beside” and μέτρον “measure”) is a quantity that serves to relate function
s and variable
s using a common variable when such a relationship would be difficult to explicate with an equation
.
Mathematical functions have one or more arguments
that are designated in the definition by variable
s, while their definition can also contain parameters. The variables are mentioned in the list of arguments that the function takes, but the parameters are not. When parameters are present, the definition actually defines a whole family of functions, one for every valid set of values of the parameters. For instance, one could define a general quadratic function by defining ;
;
here, the variable x designates the function argument, but a, b, and c are parameters that determine which quadratic function one is considering. The parameter could be incorporated into the function name to indicate its dependence on the parameter. For instance, one may define the base a logarithm by
where a is a parameter that indicates which logarithmic function is being used. It is not an argument of the function, and will, for instance, be a constant when considering the derivative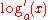 .
.
In some informal situations it is a matter of convention (or historical accident) whether some or all of the symbols in a function definition are called parameters. However, changing the status of symbols between parameter and variable changes the function as a mathematical object. For instance, the notation for the falling factorial power ,
,
defines a polynomial function of n (when k is considered a parameter), but is not a polynomial function of k (when n is considered a parameter). Indeed, in the latter case, it is only defined for non-negative integer arguments.
In the special case of parametric equations, the independent variable
s are called the parameters.
, such as a probability distribution
, the distinction between variables and parameters was described by Bard as follows:
, curve
s are often given as the image of some function. The argument of the function is invariably called "the parameter". A circle of radius 1 centered at the origin can be specified in more than one form:
A somewhat more detailed description can be found at parametric equation
.
, integrals dependent on a parameter are often considered. These are of the form
In this formula, t is the argument of the function F, and on the right-hand side the parameter on which the integral depends. When evaluating the integral, t is held constant, and so it is considered a parameter. If we are interested in the value of F for different values of t, we now consider it to be a variable. The quantity x is a dummy variable
or variable of integration (confusingly, also sometimes called a parameter of integration).
and econometrics
, the probability framework above still holds, but attention shifts to estimating the parameters of a distribution based on observed data, or testing hypotheses about them. In classical estimation these parameters are considered "fixed but unknown", but in Bayesian estimation
they are treated as random variables, and their uncertainty is described as a distribution.
It is possible to make statistical inferences without assuming a particular parametric family of probability distributions. In that case, one speaks of non-parametric statistics
as opposed to the parametric statistics
described in the previous paragraph. For example, Spearman
is a non-parametric test as it is computed from the order of the data regardless of the actual values, whereas Pearson
is a parametric test as it is computed directly from the data and can be used to derive a mathematical relationship.
Statistic
s are mathematical characteristics of samples which can be used as estimates of parameters, mathematical characteristics of the populations from which the samples are drawn. For example, the sample mean ( ) can be used as an estimate of the mean parameter (μ) of the population from which the sample was drawn.
) can be used as an estimate of the mean parameter (μ) of the population from which the sample was drawn.
In short, parameter can be defined as the numerical summary of a population
.
 In probability theory
In probability theory
, one may describe the distribution
of a random variable
as belonging to a family of probability distribution
s, distinguished from each other by the values of a finite number of parameters. For example, one talks about "a Poisson distribution
with mean value λ". The function defining the distribution (the probability mass function
) is: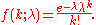
This example nicely illustrates the distinction between constants, parameters, and variables. e is Euler's Number, a fundamental mathematical constant
. The parameter λ is the mean
number of observations of some phenomenon in question, a property characteristic of the system. k is a variable, in this case the number of occurrences of the phenomenon actually observed from a particular sample. If we want to know the probability of observing k1 occurrences, we plug it into the function to get . Without altering the system, we can take multiple samples, which will have a range of values of k, but the system will always be characterized by the same λ.
. Without altering the system, we can take multiple samples, which will have a range of values of k, but the system will always be characterized by the same λ.
For instance, suppose we have a radioactive sample that emits, on average, five particles every ten minutes. We take measurements of how many particles the sample emits over ten-minute periods. The measurements will exhibit different values of k, and if the sample behaves according to Poisson statistics, then each value of k will come up in a proportion given by the probability mass function above. From measurement to measurement, however, λ remains constant at 5. If we do not alter the system, then the parameter λ is unchanged from measurement to measurement; if, on the other hand, we modulate the system by replacing the sample with a more radioactive one, then the parameter λ would increase.
Another common distribution is the normal distribution, which has as parameters the mean μ and the variance σ².
In these above examples, the distributions of the random variables are completely specified by the typpe of distribution, i.e. Poisson or normal, and the parameter values, i.e. mean and variance. In such a case, we have a parameterized distribution.a
It is possible to use the sequence of moments
(mean, mean square, ...) or cumulant
s (mean, variance, ...) as parameters for a probability distribution: see Statistical parameter
.
. In the definition of a function such as
x is a formal parameter. When the function is used as in
3 is the actual parameter value that is substituted for the formal parameter in the function definition. These concepts are discussed in a more precise way in functional programming
and its foundational disciplines, lambda calculus
and combinatory logic
.
In computing
, parameters are often called arguments, and the two words are used interchangeably. However, some computer languages such as C define argument to mean actual parameter (i.e., the value), and parameter to mean formal parameter.
(especially involving data acquisition) the term parameter sometimes loosely refers to an individual measured item. This usage isn't consistent, as sometimes the term channel refers to an individual measured item, with parameter referring to the setup information about that channel.
"Speaking generally, properties are those physical quantities which directly describe the physical attributes of the system; parameters are those combinations of the properties which suffice to determine the response of the system. Properties can have all sorts of dimensions, depending upon the system being considered; parameters are dimensionless, or have the dimension of time or its reciprocal."
The term can also be used in engineering contexts, however, as it is typically used in the physical sciences.
and microbiology
, a parameter is used to describe a discrete chemical or microbiological entity which can be assigned a value which is commonly a concentration. The value may also be a logical entity (present or absent), a statistical
result such as a 95%ile value or in some cases a subjective value
within a Principles and Parameters
framework.
, the parameters passed to (or operated on by) an open predicate are called parameters by some authors (e.g., Prawitz
, "Natural Deduction"; Paulson
, "Designing a theorem prover"). Parameters locally defined within the predicate are called variables. This extra distinction pays off when defining substitution (without this distinction special provision has to be made to avoid variable capture). Others (maybe most) just call parameters passed to (or operated on by) an open predicate variables, and when defining substitution have to distinguish between free variables and bound variables.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, logic
Logic
In philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
, linguistics
Linguistics
Linguistics is the scientific study of human language. Linguistics can be broadly broken into three categories or subfields of study: language form, language meaning, and language in context....
, environmental science
Environmental science
Environmental science is an interdisciplinary academic field that integrates physical and biological sciences, to the study of the environment, and the solution of environmental problems...
and other disciplines.
In its common meaning, the term is used to identify a characteristic, a feature, a measurable factor that can help in defining a particular system. It is an important element to take into consideration for the evaluation or for the comprehension of an event, a project or any situation.
Mathematical functions
In mathematicsMathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, and the mathematical science
Science
Science is a systematic enterprise that builds and organizes knowledge in the form of testable explanations and predictions about the universe...
s, a parameter (from Ancient Greek παρά “beside” and μέτρον “measure”) is a quantity that serves to relate function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s and variable
Variable
Variable may refer to:* Variable , a logical set of attributes* Variable , a symbol that represents a quantity in an algebraic expression....
s using a common variable when such a relationship would be difficult to explicate with an equation
Equation
An equation is a mathematical statement that asserts the equality of two expressions. In modern notation, this is written by placing the expressions on either side of an equals sign , for examplex + 3 = 5\,asserts that x+3 is equal to 5...
.
Mathematical functions have one or more arguments
Argument of a function
In mathematics, an argument of a function is a specific input in the function, also known as an independent variable. When it is clear from the context which argument is meant, the argument is often denoted by arg....
that are designated in the definition by variable
Variable (mathematics)
In mathematics, a variable is a value that may change within the scope of a given problem or set of operations. In contrast, a constant is a value that remains unchanged, though often unknown or undetermined. The concepts of constants and variables are fundamental to many areas of mathematics and...
s, while their definition can also contain parameters. The variables are mentioned in the list of arguments that the function takes, but the parameters are not. When parameters are present, the definition actually defines a whole family of functions, one for every valid set of values of the parameters. For instance, one could define a general quadratic function by defining
 ;
;here, the variable x designates the function argument, but a, b, and c are parameters that determine which quadratic function one is considering. The parameter could be incorporated into the function name to indicate its dependence on the parameter. For instance, one may define the base a logarithm by

where a is a parameter that indicates which logarithmic function is being used. It is not an argument of the function, and will, for instance, be a constant when considering the derivative
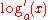 .
.In some informal situations it is a matter of convention (or historical accident) whether some or all of the symbols in a function definition are called parameters. However, changing the status of symbols between parameter and variable changes the function as a mathematical object. For instance, the notation for the falling factorial power
 ,
,defines a polynomial function of n (when k is considered a parameter), but is not a polynomial function of k (when n is considered a parameter). Indeed, in the latter case, it is only defined for non-negative integer arguments.
In the special case of parametric equations, the independent variable
Independent variable
The terms "dependent variable" and "independent variable" are used in similar but subtly different ways in mathematics and statistics as part of the standard terminology in those subjects...
s are called the parameters.
Examples
- In a section on frequently misused words in his book The Writer's Art, James J. KilpatrickJames J. KilpatrickJames Jackson Kilpatrick was an American editorial columnist and grammarian. He was a legal abstractionist, a social conservative, and an economic libertarian according to Harvard ....
quoted a letter from a correspondent, giving examples to illustrate the correct use of the word parameter:
- A parametric equaliserEqualizationEqualization, is the process of adjusting the balance between frequency components within an electronic signal. The most well known use of equalization is in sound recording and reproduction but there are many other applications in electronics and telecommunications. The circuit or equipment used...
is an audio filterAudio filterAn audio filter is a frequency dependent amplifier circuit, working in the audio frequency range, 0 Hz to beyond 20 kHz. Many types of filters exist for applications including graphic equalizers, synthesizers, sound effects, CD players and virtual reality systems.Being a frequency dependent...
that allows the frequencyFrequencyFrequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
of maximum cut or boost to be set by one control, and the size of the cut or boost by another. These settings, the frequency level of the peak or trough, are two of the parameters of a frequency response curve, and in a two-control equaliser they completely describe the curve. More elaborate parametric equalisers may allow other parameters to be varied, such as skew. These parameters each describe some aspect of the response curve seen as a whole, over all frequencies. A graphic equaliserEqualizationEqualization, is the process of adjusting the balance between frequency components within an electronic signal. The most well known use of equalization is in sound recording and reproduction but there are many other applications in electronics and telecommunications. The circuit or equipment used...
provides individual level controls for various frequency bands, each of which acts only on that particular frequency band.
- If asked to imagine the graph of the relationship y = ax2, one typically visualizes a range of values of x, but only one value of a. Of course a different value of a can be used, generating a different relation between x and y. Thus a is considered to be a parameter: it is less variable than the variable x or y, but it is not an explicit constant like the exponent 2. More precisely, changing the parameter a gives a different (though related) problem, whereas the variations of the variables x and y (and their interrelation) are part of the problem itself.
- In calculating income based on wage and hours worked (income equals wage multiplied by hours worked), it is typically assumed that the number of hours worked is easily changed, but the wage is more static. This makes 'wage' a parameter, 'hours worked' an independent variableIndependent variableThe terms "dependent variable" and "independent variable" are used in similar but subtly different ways in mathematics and statistics as part of the standard terminology in those subjects...
, and 'income' a dependent variable.
Mathematical models
In the context of a mathematical modelMathematical model
A mathematical model is a description of a system using mathematical concepts and language. The process of developing a mathematical model is termed mathematical modeling. Mathematical models are used not only in the natural sciences and engineering disciplines A mathematical model is a...
, such as a probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
, the distinction between variables and parameters was described by Bard as follows:
- We refer to the relations which supposedly describe a certain physical situation, as a model. Typically, a model consists of one or more equations. The quantities appearing in the equations we classify into variables and parameters. The distinction between these is not always clear cut, and it frequently depends on the context in which the variables appear. Usually a model is designed to explain the relationships that exist among quantities which can be measured independently in an experiment; these are the variables of the model. To formulate these relationships, however, one frequently introduces "constants" which stand for inherent properties of nature (or of the materials and equipment used in a given experiment). These are the parameters.
Analytic geometry
In analytic geometryAnalytic geometry
Analytic geometry, or analytical geometry has two different meanings in mathematics. The modern and advanced meaning refers to the geometry of analytic varieties...
, curve
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
s are often given as the image of some function. The argument of the function is invariably called "the parameter". A circle of radius 1 centered at the origin can be specified in more than one form:
- implicit form

- parametric form

- where t is the parameter.
A somewhat more detailed description can be found at parametric equation
Parametric equation
In mathematics, parametric equation is a method of defining a relation using parameters. A simple kinematic example is when one uses a time parameter to determine the position, velocity, and other information about a body in motion....
.
Mathematical analysis
In mathematical analysisMathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, integrals dependent on a parameter are often considered. These are of the form

In this formula, t is the argument of the function F, and on the right-hand side the parameter on which the integral depends. When evaluating the integral, t is held constant, and so it is considered a parameter. If we are interested in the value of F for different values of t, we now consider it to be a variable. The quantity x is a dummy variable
Dummy variable
In statistics and econometrics, particularly in regression analysis, a dummy variable is one that takes the values 0 or 1 to indicate the absence or presence of some categorical effect that may be expected to shift the outcome...
or variable of integration (confusingly, also sometimes called a parameter of integration).
Statistics and econometrics
In statisticsStatistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
and econometrics
Econometrics
Econometrics has been defined as "the application of mathematics and statistical methods to economic data" and described as the branch of economics "that aims to give empirical content to economic relations." More precisely, it is "the quantitative analysis of actual economic phenomena based on...
, the probability framework above still holds, but attention shifts to estimating the parameters of a distribution based on observed data, or testing hypotheses about them. In classical estimation these parameters are considered "fixed but unknown", but in Bayesian estimation
Bayesian probability
Bayesian probability is one of the different interpretations of the concept of probability and belongs to the category of evidential probabilities. The Bayesian interpretation of probability can be seen as an extension of logic that enables reasoning with propositions, whose truth or falsity is...
they are treated as random variables, and their uncertainty is described as a distribution.
It is possible to make statistical inferences without assuming a particular parametric family of probability distributions. In that case, one speaks of non-parametric statistics
Non-parametric statistics
In statistics, the term non-parametric statistics has at least two different meanings:The first meaning of non-parametric covers techniques that do not rely on data belonging to any particular distribution. These include, among others:...
as opposed to the parametric statistics
Parametric statistics
Parametric statistics is a branch of statistics that assumes that the data has come from a type of probability distribution and makes inferences about the parameters of the distribution. Most well-known elementary statistical methods are parametric....
described in the previous paragraph. For example, Spearman
Spearman's rank correlation coefficient
In statistics, Spearman's rank correlation coefficient or Spearman's rho, named after Charles Spearman and often denoted by the Greek letter \rho or as r_s, is a non-parametric measure of statistical dependence between two variables. It assesses how well the relationship between two variables can...
is a non-parametric test as it is computed from the order of the data regardless of the actual values, whereas Pearson
Pearson product-moment correlation coefficient
In statistics, the Pearson product-moment correlation coefficient is a measure of the correlation between two variables X and Y, giving a value between +1 and −1 inclusive...
is a parametric test as it is computed directly from the data and can be used to derive a mathematical relationship.
Statistic
Statistic
A statistic is a single measure of some attribute of a sample . It is calculated by applying a function to the values of the items comprising the sample which are known together as a set of data.More formally, statistical theory defines a statistic as a function of a sample where the function...
s are mathematical characteristics of samples which can be used as estimates of parameters, mathematical characteristics of the populations from which the samples are drawn. For example, the sample mean (
 ) can be used as an estimate of the mean parameter (μ) of the population from which the sample was drawn.
) can be used as an estimate of the mean parameter (μ) of the population from which the sample was drawn.In short, parameter can be defined as the numerical summary of a population
Population
A population is all the organisms that both belong to the same group or species and live in the same geographical area. The area that is used to define a sexual population is such that inter-breeding is possible between any pair within the area and more probable than cross-breeding with individuals...
.
Probability theory

Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, one may describe the distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
of a random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
as belonging to a family of probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
s, distinguished from each other by the values of a finite number of parameters. For example, one talks about "a Poisson distribution
Poisson distribution
In probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently of the time since...
with mean value λ". The function defining the distribution (the probability mass function
Probability mass function
In probability theory and statistics, a probability mass function is a function that gives the probability that a discrete random variable is exactly equal to some value...
) is:
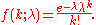
This example nicely illustrates the distinction between constants, parameters, and variables. e is Euler's Number, a fundamental mathematical constant
Mathematical constant
A mathematical constant is a special number, usually a real number, that is "significantly interesting in some way". Constants arise in many different areas of mathematics, with constants such as and occurring in such diverse contexts as geometry, number theory and calculus.What it means for a...
. The parameter λ is the mean
Mean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
number of observations of some phenomenon in question, a property characteristic of the system. k is a variable, in this case the number of occurrences of the phenomenon actually observed from a particular sample. If we want to know the probability of observing k1 occurrences, we plug it into the function to get
 . Without altering the system, we can take multiple samples, which will have a range of values of k, but the system will always be characterized by the same λ.
. Without altering the system, we can take multiple samples, which will have a range of values of k, but the system will always be characterized by the same λ.For instance, suppose we have a radioactive sample that emits, on average, five particles every ten minutes. We take measurements of how many particles the sample emits over ten-minute periods. The measurements will exhibit different values of k, and if the sample behaves according to Poisson statistics, then each value of k will come up in a proportion given by the probability mass function above. From measurement to measurement, however, λ remains constant at 5. If we do not alter the system, then the parameter λ is unchanged from measurement to measurement; if, on the other hand, we modulate the system by replacing the sample with a more radioactive one, then the parameter λ would increase.
Another common distribution is the normal distribution, which has as parameters the mean μ and the variance σ².
In these above examples, the distributions of the random variables are completely specified by the typpe of distribution, i.e. Poisson or normal, and the parameter values, i.e. mean and variance. In such a case, we have a parameterized distribution.a
It is possible to use the sequence of moments
Moment (mathematics)
In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
(mean, mean square, ...) or cumulant
Cumulant
In probability theory and statistics, the cumulants κn of a probability distribution are a set of quantities that provide an alternative to the moments of the distribution. The moments determine the cumulants in the sense that any two probability distributions whose moments are identical will have...
s (mean, variance, ...) as parameters for a probability distribution: see Statistical parameter
Statistical parameter
A statistical parameter is a parameter that indexes a family of probability distributions. It can be regarded as a numerical characteristic of a population or a model....
.
Computer science
When the terms formal parameter and actual parameter are used, they generally correspond with the definitions used in computer scienceParameter (computer science)
In computer programming, a parameter is a special kind of variable, used in a subroutine to refer to one of the pieces of data provided as input to the subroutine. These pieces of data are called arguments...
. In the definition of a function such as
- f(x) = x + 2,
x is a formal parameter. When the function is used as in
- y = f(3) + 5 or just the value of f(3),
3 is the actual parameter value that is substituted for the formal parameter in the function definition. These concepts are discussed in a more precise way in functional programming
Functional programming
In computer science, functional programming is a programming paradigm that treats computation as the evaluation of mathematical functions and avoids state and mutable data. It emphasizes the application of functions, in contrast to the imperative programming style, which emphasizes changes in state...
and its foundational disciplines, lambda calculus
Lambda calculus
In mathematical logic and computer science, lambda calculus, also written as λ-calculus, is a formal system for function definition, function application and recursion. The portion of lambda calculus relevant to computation is now called the untyped lambda calculus...
and combinatory logic
Combinatory logic
Combinatory logic is a notation introduced by Moses Schönfinkel and Haskell Curry to eliminate the need for variables in mathematical logic. It has more recently been used in computer science as a theoretical model of computation and also as a basis for the design of functional programming...
.
In computing
Computing
Computing is usually defined as the activity of using and improving computer hardware and software. It is the computer-specific part of information technology...
, parameters are often called arguments, and the two words are used interchangeably. However, some computer languages such as C define argument to mean actual parameter (i.e., the value), and parameter to mean formal parameter.
Engineering
In engineeringEngineering
Engineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...
(especially involving data acquisition) the term parameter sometimes loosely refers to an individual measured item. This usage isn't consistent, as sometimes the term channel refers to an individual measured item, with parameter referring to the setup information about that channel.
"Speaking generally, properties are those physical quantities which directly describe the physical attributes of the system; parameters are those combinations of the properties which suffice to determine the response of the system. Properties can have all sorts of dimensions, depending upon the system being considered; parameters are dimensionless, or have the dimension of time or its reciprocal."
The term can also be used in engineering contexts, however, as it is typically used in the physical sciences.
Environmental science
In environmental science and particularly in chemistryChemistry
Chemistry is the science of matter, especially its chemical reactions, but also its composition, structure and properties. Chemistry is concerned with atoms and their interactions with other atoms, and particularly with the properties of chemical bonds....
and microbiology
Microbiology
Microbiology is the study of microorganisms, which are defined as any microscopic organism that comprises either a single cell , cell clusters or no cell at all . This includes eukaryotes, such as fungi and protists, and prokaryotes...
, a parameter is used to describe a discrete chemical or microbiological entity which can be assigned a value which is commonly a concentration. The value may also be a logical entity (present or absent), a statistical
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
result such as a 95%ile value or in some cases a subjective value
Linguistics
Within linguistics, the word "parameter" is almost exclusively used to denote a binary switch in a Universal GrammarUniversal grammar
Universal grammar is a theory in linguistics that suggests that there are properties that all possible natural human languages have.Usually credited to Noam Chomsky, the theory suggests that some rules of grammar are hard-wired into the brain, and manifest themselves without being taught...
within a Principles and Parameters
Principles and parameters
Principles and parameters is a framework within generative linguistics in which the syntax of a natural language is described in accordance with general principles and specific parameters that for particular languages are either turned on or off...
framework.
Logic
In logicLogic
In philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
, the parameters passed to (or operated on by) an open predicate are called parameters by some authors (e.g., Prawitz
Dag Prawitz
Dag Prawitz is a Swedish philosopher and logician. He is best known for his work on proof theory and the foundations of natural deduction....
, "Natural Deduction"; Paulson
Lawrence Paulson
Lawrence Charles Paulson is a professor at the University of Cambridge Computer Laboratory and a fellow of Clare College. He lectures courses on the foundations of computer science, logic and proof among others. He is best known for the cornerstone text on the programming language ML, ML for the...
, "Designing a theorem prover"). Parameters locally defined within the predicate are called variables. This extra distinction pays off when defining substitution (without this distinction special provision has to be made to avoid variable capture). Others (maybe most) just call parameters passed to (or operated on by) an open predicate variables, and when defining substitution have to distinguish between free variables and bound variables.
See also
- One-parameter groupOne-parameter groupIn mathematics, a one-parameter group or one-parameter subgroup usually means a continuous group homomorphismfrom the real line R to some other topological group G...
- ParametrizationParametrizationParametrization is the process of deciding and defining the parameters necessary for a complete or relevant specification of a model or geometric object....
(i.e., coordinate systemCoordinate systemIn geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...
) - Parametrization (climate)Parametrization (climate)Parameterization in a weather or climate model within numerical weather prediction refers to the method of replacing processes that are too small-scale or complex to be physically represented in the model by a simplified process. This can be contrasted with other processes—e.g., large-scale flow of...
- Parsimony (with regards to the trade-off of many or few parameters in data fitting)

