
Regular representation
Encyclopedia
In mathematics
, and in particular the theory of group representation
s, the regular representation of a group G is the linear representation afforded by the group action
of G on itself by translation.
One distinguishes the left regular representation λ given by left translation and the right regular representation ρ given by the inverse of right translation.
G, the left regular representation λ (over a field
K) is a linear representation on the K-vector space
V whose basis
are the elements of G. Given g ∈ G, λ(g) is the linear map determined by its action on the basis by left translation by g, i.e.
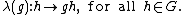
For the right regular representation ρ, an inversion must occur in order to satisfy the axioms of a representation. Specifically, given g ∈ G, ρ(g) is the linear map on V determined by its action on the basis by right translation by g−1, i.e.
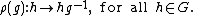
Alternatively, these representations can be defined on the K-vector space W of all functions . It is in this form that the regular representation is generalized to topological group
s such as Lie group
s.
The specific definition in terms of W is as follows. Given a function and an element g ∈ G,
and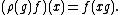
it is characterised as having a single orbit and stabilizer
the identity subgroup {e} of G. The regular representation of G, for a given field K, is the linear representation made by taking this permutation representation as a set of basis vectors of a vector space
over K. The significance is that while the permutation representation doesn't decompose - it is transitive
- the regular representation in general breaks up into smaller representations. For example if G is a finite group and K is the complex number
field, the regular representation decomposes as a direct sum of irreducible representations, with each irreducible representation appearing in the decomposition with multiplicity its dimension. The number of these irreducibles is equal to the number of conjugacy class
es of G.
The article on group algebra
s articulates the regular representation for finite group
s, as well as showing how the regular representation can be taken to be a module
.
K[G] is considered as a module over itself. (There is a choice here of left-action or right-action, but that is not of importance except for notation.) If G is finite and the characteristic
of K doesn't divide |G|, this is a semisimple ring and we are looking at its left (right) ring ideals. This theory has been studied in great depth. It is known in particular that the direct sum decomposition of the regular representation contains a representative of every isomorphism class of irreducible linear representations of G over K. You can say that the regular representation is comprehensive for representation theory, in this case. The modular case, when the characteristic of K does divide |G|, is harder mainly because with K[G] not semisimple, and a representation can fail to be irreducible without splitting as a direct sum.
C generated by g of order n, the matrix form of an element of K[C] acting on K[C] by multiplication takes a distinctive form known as a circulant matrix
, in which each row is a shift to the right of the one above (in cyclic order, i.e. with the right-most element appearing on the left), when referred to the natural basis
When the field K contains a primitive n-th root of unity, one can diagonalise
the representation of C by writing down n linearly independent simultaneous eigenvectors for all the n×n circulants. In fact if ζ is any n-th root of unity, the element
is an eigenvector for the action of g by multiplication, with eigenvalue
and so also an eigenvector of all powers of g, and their linear combinations.
This is the explicit form in this case of the abstract result that over an algebraically closed field
K (such as the complex number
s) the regular representation of G is completely reducible, provided that the characteristic of K (if it is a prime number p) doesn't divide the order of G. That is called Maschke's theorem
. In this case the condition on the characteristic is implied by the existence of a primitive n-th root of unity, which cannot happen in the case of prime characteristic p dividing n.
Circulant determinant
s were first encountered in nineteenth century mathematics, and the consequence of their diagonalisation drawn. Namely, the determinant of a circulant is the product of the n eigenvalues for the n eigenvectors described above. The basic work of Frobenius
on group representation
s started with the motivation of finding analogous factorisations of the group determinants for any finite G; that is, the determinants of arbitrary matrices representing elements of K[G] acting by multiplication on the basis elements given by g in G. Unless G is abelian
, the factorisation must contain non-linear factors corresponding to irreducible representations of G of degree > 1.
case. If G is a Lie group but not compact nor abelian
, this is a difficult matter of harmonic analysis
. The locally compact abelian case is part of the Pontryagin duality
theory.
it is shown that for a field L, and a finite group G of automorphism
s of L, the fixed field K of G has [L:K] = |G|. In fact we can say more: L viewed as a K[G]-module is the regular representation. This is the content of the normal basis theorem, a normal basis being an element x of L such that the g(x) for g in G are a vector space
basis for L over K. Such x exist, and each one gives a K[G]-isomorphism from L to K[G]. From the point of view of algebraic number theory
it is of interest to study normal integral bases, where we try to replace L and K by the rings of algebraic integer
s they contain. One can see already in the case of the Gaussian integer
s that such bases may not exist: a + bi and a − bi can never form a Z-module basis of Z[i] because 1 cannot be an integer combination. The reasons are studied in depth in Galois module
theory.
A, it doesn't immediately make sense to ask about the relation between A as left-module over itself, and as right-module. In the group case, the mapping on basis elements g of K[G] defined by taking the inverse element gives an isomorphism of K[G] to its opposite ring. For A general, such a structure is called a Frobenius algebra
. As the name implies, these were introduced by Frobenius
in the nineteenth century. They have been shown to be related to topological quantum field theory
in 1 + 1 dimensions.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, and in particular the theory of group representation
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
s, the regular representation of a group G is the linear representation afforded by the group action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
of G on itself by translation.
One distinguishes the left regular representation λ given by left translation and the right regular representation ρ given by the inverse of right translation.
Finite groups
For a finite groupFinite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
G, the left regular representation λ (over a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
K) is a linear representation on the K-vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
V whose basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
are the elements of G. Given g ∈ G, λ(g) is the linear map determined by its action on the basis by left translation by g, i.e.
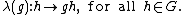
For the right regular representation ρ, an inversion must occur in order to satisfy the axioms of a representation. Specifically, given g ∈ G, ρ(g) is the linear map on V determined by its action on the basis by right translation by g−1, i.e.
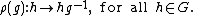
Alternatively, these representations can be defined on the K-vector space W of all functions . It is in this form that the regular representation is generalized to topological group
Topological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
s such as Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s.
The specific definition in terms of W is as follows. Given a function and an element g ∈ G,

and
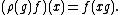
Significance of the regular representation of a group
To say that G acts on itself by multiplication is tautological. If we consider this action as a permutation representationGroup action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
it is characterised as having a single orbit and stabilizer
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
the identity subgroup {e} of G. The regular representation of G, for a given field K, is the linear representation made by taking this permutation representation as a set of basis vectors of a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
over K. The significance is that while the permutation representation doesn't decompose - it is transitive
Transitivity (mathematics)
-In grammar:* Intransitive verb* Transitive verb, when a verb takes an object* Transitivity -In logic and mathematics:* Arc-transitive graph* Edge-transitive graph* Ergodic theory, a group action that is metrically transitive* Vertex-transitive graph...
- the regular representation in general breaks up into smaller representations. For example if G is a finite group and K is the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
field, the regular representation decomposes as a direct sum of irreducible representations, with each irreducible representation appearing in the decomposition with multiplicity its dimension. The number of these irreducibles is equal to the number of conjugacy class
Conjugacy class
In mathematics, especially group theory, the elements of any group may be partitioned into conjugacy classes; members of the same conjugacy class share many properties, and study of conjugacy classes of non-abelian groups reveals many important features of their structure...
es of G.
The article on group algebra
Group algebra
In mathematics, the group algebra is any of various constructions to assign to a locally compact group an operator algebra , such that representations of the algebra are related to representations of the group...
s articulates the regular representation for finite group
Finite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
s, as well as showing how the regular representation can be taken to be a module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
.
Module theory point of view
To put the construction more abstractly, the group ringGroup ring
In algebra, a group ring is a free module and at the same time a ring, constructed in a natural way from any given ring and any given group. As a free module, its ring of scalars is the given ring and its basis is one-to-one with the given group. As a ring, its addition law is that of the free...
K[G] is considered as a module over itself. (There is a choice here of left-action or right-action, but that is not of importance except for notation.) If G is finite and the characteristic
Characteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
of K doesn't divide |G|, this is a semisimple ring and we are looking at its left (right) ring ideals. This theory has been studied in great depth. It is known in particular that the direct sum decomposition of the regular representation contains a representative of every isomorphism class of irreducible linear representations of G over K. You can say that the regular representation is comprehensive for representation theory, in this case. The modular case, when the characteristic of K does divide |G|, is harder mainly because with K[G] not semisimple, and a representation can fail to be irreducible without splitting as a direct sum.
Structure for finite cyclic groups
For a cyclic groupCyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
C generated by g of order n, the matrix form of an element of K[C] acting on K[C] by multiplication takes a distinctive form known as a circulant matrix
Circulant matrix
In linear algebra, a circulant matrix is a special kind of Toeplitz matrix where each row vector is rotated one element to the right relative to the preceding row vector. In numerical analysis, circulant matrices are important because they are diagonalized by a discrete Fourier transform, and hence...
, in which each row is a shift to the right of the one above (in cyclic order, i.e. with the right-most element appearing on the left), when referred to the natural basis
- 1, g, g2, ..., gn−1.
When the field K contains a primitive n-th root of unity, one can diagonalise
Diagonalizable matrix
In linear algebra, a square matrix A is called diagonalizable if it is similar to a diagonal matrix, i.e., if there exists an invertible matrix P such that P −1AP is a diagonal matrix...
the representation of C by writing down n linearly independent simultaneous eigenvectors for all the n×n circulants. In fact if ζ is any n-th root of unity, the element
- 1 + ζg + ζ2g2 + ... + ζn−1gn−1
is an eigenvector for the action of g by multiplication, with eigenvalue
- ζ−1
and so also an eigenvector of all powers of g, and their linear combinations.
This is the explicit form in this case of the abstract result that over an algebraically closed field
Algebraically closed field
In mathematics, a field F is said to be algebraically closed if every polynomial with one variable of degree at least 1, with coefficients in F, has a root in F.-Examples:...
K (such as the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s) the regular representation of G is completely reducible, provided that the characteristic of K (if it is a prime number p) doesn't divide the order of G. That is called Maschke's theorem
Maschke's theorem
In mathematics, Maschke's theorem, named after Heinrich Maschke, is a theorem in group representation theory that concerns the decomposition of representations of a finite group into irreducible pieces...
. In this case the condition on the characteristic is implied by the existence of a primitive n-th root of unity, which cannot happen in the case of prime characteristic p dividing n.
Circulant determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
s were first encountered in nineteenth century mathematics, and the consequence of their diagonalisation drawn. Namely, the determinant of a circulant is the product of the n eigenvalues for the n eigenvectors described above. The basic work of Frobenius
Ferdinand Georg Frobenius
Ferdinand Georg Frobenius was a German mathematician, best known for his contributions to the theory of differential equations and to group theory...
on group representation
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
s started with the motivation of finding analogous factorisations of the group determinants for any finite G; that is, the determinants of arbitrary matrices representing elements of K[G] acting by multiplication on the basis elements given by g in G. Unless G is abelian
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
, the factorisation must contain non-linear factors corresponding to irreducible representations of G of degree > 1.
Topological group case
For a topological group G, the regular representation in the above sense should be replaced by a suitable space of functions on G, with G acting by translation. See Peter-Weyl theorem for the compactCompact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
case. If G is a Lie group but not compact nor abelian
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
, this is a difficult matter of harmonic analysis
Harmonic analysis
Harmonic analysis is the branch of mathematics that studies the representation of functions or signals as the superposition of basic waves. It investigates and generalizes the notions of Fourier series and Fourier transforms...
. The locally compact abelian case is part of the Pontryagin duality
Pontryagin duality
In mathematics, specifically in harmonic analysis and the theory of topological groups, Pontryagin duality explains the general properties of the Fourier transform on locally compact groups, such as R, the circle or finite cyclic groups.-Introduction:...
theory.
Normal bases in Galois theory
In Galois theoryGalois theory
In mathematics, more specifically in abstract algebra, Galois theory, named after Évariste Galois, provides a connection between field theory and group theory...
it is shown that for a field L, and a finite group G of automorphism
Automorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
s of L, the fixed field K of G has [L:K] = |G|. In fact we can say more: L viewed as a K[G]-module is the regular representation. This is the content of the normal basis theorem, a normal basis being an element x of L such that the g(x) for g in G are a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
basis for L over K. Such x exist, and each one gives a K[G]-isomorphism from L to K[G]. From the point of view of algebraic number theory
Algebraic number theory
Algebraic number theory is a major branch of number theory which studies algebraic structures related to algebraic integers. This is generally accomplished by considering a ring of algebraic integers O in an algebraic number field K/Q, and studying their algebraic properties such as factorization,...
it is of interest to study normal integral bases, where we try to replace L and K by the rings of algebraic integer
Algebraic integer
In number theory, an algebraic integer is a complex number that is a root of some monic polynomial with coefficients in . The set of all algebraic integers is closed under addition and multiplication and therefore is a subring of complex numbers denoted by A...
s they contain. One can see already in the case of the Gaussian integer
Gaussian integer
In number theory, a Gaussian integer is a complex number whose real and imaginary part are both integers. The Gaussian integers, with ordinary addition and multiplication of complex numbers, form an integral domain, usually written as Z[i]. The Gaussian integers are a special case of the quadratic...
s that such bases may not exist: a + bi and a − bi can never form a Z-module basis of Z[i] because 1 cannot be an integer combination. The reasons are studied in depth in Galois module
Galois module
In mathematics, a Galois module is a G-module where G is the Galois group of some extension of fields. The term Galois representation is frequently used when the G-module is a vector space over a field or a free module over a ring, but can also be used as a synonym for G-module...
theory.
More general algebras
The regular representation of a group ring is such that the left-hand and right-hand regular representations give isomorphic modules (and we often need not distinguish the cases). Given an algebra over a fieldAlgebra over a field
In mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...
A, it doesn't immediately make sense to ask about the relation between A as left-module over itself, and as right-module. In the group case, the mapping on basis elements g of K[G] defined by taking the inverse element gives an isomorphism of K[G] to its opposite ring. For A general, such a structure is called a Frobenius algebra
Frobenius algebra
In mathematics, especially in the fields of representation theory and module theory, a Frobenius algebra is a finite dimensional unital associative algebra with a special kind of bilinear form which gives the algebras particularly nice duality theories. Frobenius algebras began to be studied in...
. As the name implies, these were introduced by Frobenius
Ferdinand Georg Frobenius
Ferdinand Georg Frobenius was a German mathematician, best known for his contributions to the theory of differential equations and to group theory...
in the nineteenth century. They have been shown to be related to topological quantum field theory
Topological quantum field theory
A topological quantum field theory is a quantum field theory which computes topological invariants....
in 1 + 1 dimensions.

