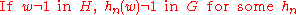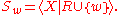Word problem for groups
Encyclopedia
In mathematics
, especially in the area of abstract algebra
known as combinatorial group theory
, the word problem for a finitely generated group G is the algorithmic problem of deciding whether two words in the generators represent the same element. More precisely, if A is a finite set of generators for G then the word problem is the membership problem for the formal language
of all words in A and a formal set of inverses that map to the identity under the natural map from the free monoid with involution on A to the group G. If B is another finite generating set for G, then the word problem over the generating set B is equivalent to the word problem over the generating set A. Thus one can speak unambiguously of the decidability of the word problem for the finitely generated group G.
The related but different uniform word problem for a class K of recursively presented groups is the algorithmic problem of deciding, given as input a presentation
P for a group G in the class K and two words in the generators of G, whether the words represent the same element of G. Some authors require the class K to be definable by a recursively enumerable set of presentations.
s. These usually implicitly solve the word problem for the groups in question. In 1911 Max Dehn
proposed that the word problem was an important area of study in its own right, , together with the conjugacy problem
and the group isomorphism problem
. In 1912 he gave an algorithm that solves both the word and conjugacy problem for the fundamental group
s of closed orientable two-dimensional manifolds of genus greater than or equal to 2, . Subsequent authors have greatly extended Dehn's algorithm and applied it to a wide range of group theoretic decision problem
s.
It was shown by Pyotr Novikov in 1955 that there exists a finitely generated (in fact, a finitely presented) group G such that the word problem for G is undecidable
. It follows immediately that the uniform word problem is also undecidable. A different proof was obtained by Boone in 1958.
The word problem was one of the first examples of an unsolvable problem to be found not in mathematical logic
or the theory of algorithms, but in one of the central branches of classical mathematics, algebra
. As a result of its unsolvability, several other problems in combinatorial group theory have been shown to be unsolvable as well.
It is important to realize that the word problem is in fact solvable for many groups G. For example, polycyclic group
s have solvable word problems since the normal form of an arbitrary word in a polycyclic presentation is readily computable; other algorithms for groups may, in suitable circumstances, also solve the word problem, see the Todd–Coxeter algorithm and the Knuth–Bendix completion algorithm. On the other hand the fact that a particular algorithm does not solve the word problem for a particular group does not show that the group has unsolvable word problem. For instance Dehn's algorithm does not solve the word problem for the fundamental group of the torus
. However this group is the direct product of two infinite cyclic groups and so has solvable word problem.
question, for literal strings, . For a presentation P of a group G, P will specify a certain number of generators
for G. We need to introduce one letter for x and another (for convenience) for the group element represented by x−1. Call these letters (twice as many as the generators) the alphabet A for our problem. Then each element in G is represented in some way by a product
of symbols from A, of some length, multiplied in G. The string of length 0 (null string
) stands for the identity element
e of G. The crux of the whole problem is to be able to recognise all the ways e can be represented, given some relations.
The effect of the relations in G is to make various such strings represent the same element of G. In fact the relations provide a list of strings that can be either introduced where we want, or cancelled out whenever we see them, without changing the 'value', i.e. the group element that is the result of the multiplication.
For a simple example, take the presentation ⟨xy|x3⟩. Writing y for the inverse of x, we have possible strings combining any number of x and y symbols. Whenever we see xxx, or xy or yx we may strike these out. We should also remember to strike out yyy; this says that since the cube of x is the identity element of G, so is the cube of the inverse of x. Under these conditions the word problem becomes easy. First reduce strings to e, x, xx, y or yy. Then note that we may also multiply by xxx, so we can convert yy to x. The result is that we can prove that the word problem here, for what is the cyclic group
of order three, is solvable.
This is not, however, the typical case. For the example, we have a canonical form
available that reduces any string to one of length at most three, by decreasing the length monotonically. In general, it is not true that one can get a canonical form for the elements, by stepwise cancellation. One may have to use relations to expand a string many-fold, in order eventually to find a cancellation that brings the length right down.
The upshot is, in the worst case, that the relation between strings that says they are equal in G is not decidable
.
Examples with unsolvable word problems are also known:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, especially in the area of abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
known as combinatorial group theory
Combinatorial group theory
In mathematics, combinatorial group theory is the theory of free groups, and the concept of a presentation of a group by generators and relations...
, the word problem for a finitely generated group G is the algorithmic problem of deciding whether two words in the generators represent the same element. More precisely, if A is a finite set of generators for G then the word problem is the membership problem for the formal language
Formal language
A formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
of all words in A and a formal set of inverses that map to the identity under the natural map from the free monoid with involution on A to the group G. If B is another finite generating set for G, then the word problem over the generating set B is equivalent to the word problem over the generating set A. Thus one can speak unambiguously of the decidability of the word problem for the finitely generated group G.
The related but different uniform word problem for a class K of recursively presented groups is the algorithmic problem of deciding, given as input a presentation
Presentation of a group
In mathematics, one method of defining a group is by a presentation. One specifies a set S of generators so that every element of the group can be written as a product of powers of some of these generators, and a set R of relations among those generators...
P for a group G in the class K and two words in the generators of G, whether the words represent the same element of G. Some authors require the class K to be definable by a recursively enumerable set of presentations.
History
Throughout the history of the subject, computations in groups have been carried out using various normal formNormal form
Normal form may refer to:* Normal form * Normal form * Normal form * Normal form In formal language theory:* Beta normal form* Chomsky normal form* Greibach normal form* Kuroda normal form...
s. These usually implicitly solve the word problem for the groups in question. In 1911 Max Dehn
Max Dehn
Max Dehn was a German American mathematician and a student of David Hilbert. He is most famous for his work in geometry, topology and geometric group theory...
proposed that the word problem was an important area of study in its own right, , together with the conjugacy problem
Conjugacy problem
In abstract algebra, the conjugacy problem for a group G with a given presentation is the decision problem of determining, given two words x and y in G, whether or not they represent conjugate elements of G...
and the group isomorphism problem
Group isomorphism problem
In abstract algebra, the group isomorphism problem is the decision problem of determining whether two group presentations present isomorphic groups....
. In 1912 he gave an algorithm that solves both the word and conjugacy problem for the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
s of closed orientable two-dimensional manifolds of genus greater than or equal to 2, . Subsequent authors have greatly extended Dehn's algorithm and applied it to a wide range of group theoretic decision problem
Decision problem
In computability theory and computational complexity theory, a decision problem is a question in some formal system with a yes-or-no answer, depending on the values of some input parameters. For example, the problem "given two numbers x and y, does x evenly divide y?" is a decision problem...
s.
It was shown by Pyotr Novikov in 1955 that there exists a finitely generated (in fact, a finitely presented) group G such that the word problem for G is undecidable
Undecidable problem
In computability theory and computational complexity theory, an undecidable problem is a decision problem for which it is impossible to construct a single algorithm that always leads to a correct yes-or-no answer....
. It follows immediately that the uniform word problem is also undecidable. A different proof was obtained by Boone in 1958.
The word problem was one of the first examples of an unsolvable problem to be found not in mathematical logic
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
or the theory of algorithms, but in one of the central branches of classical mathematics, algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
. As a result of its unsolvability, several other problems in combinatorial group theory have been shown to be unsolvable as well.
It is important to realize that the word problem is in fact solvable for many groups G. For example, polycyclic group
Polycyclic group
In mathematics, a polycyclic group is a solvable group that satisfies the maximal condition on subgroups...
s have solvable word problems since the normal form of an arbitrary word in a polycyclic presentation is readily computable; other algorithms for groups may, in suitable circumstances, also solve the word problem, see the Todd–Coxeter algorithm and the Knuth–Bendix completion algorithm. On the other hand the fact that a particular algorithm does not solve the word problem for a particular group does not show that the group has unsolvable word problem. For instance Dehn's algorithm does not solve the word problem for the fundamental group of the torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
. However this group is the direct product of two infinite cyclic groups and so has solvable word problem.
A more concrete description
In more concrete terms, the uniform word problem can be expressed as a rewritingRewriting
In mathematics, computer science, and logic, rewriting covers a wide range of methods of replacing subterms of a formula with other terms. What is considered are rewriting systems...
question, for literal strings, . For a presentation P of a group G, P will specify a certain number of generators
- x, y, z, ...
for G. We need to introduce one letter for x and another (for convenience) for the group element represented by x−1. Call these letters (twice as many as the generators) the alphabet A for our problem. Then each element in G is represented in some way by a product
- abc ... pqr
of symbols from A, of some length, multiplied in G. The string of length 0 (null string
Empty string
In computer science and formal language theory, the empty string is the unique string of length zero. It is denoted with λ or sometimes Λ or ε....
) stands for the identity element
Identity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
e of G. The crux of the whole problem is to be able to recognise all the ways e can be represented, given some relations.
The effect of the relations in G is to make various such strings represent the same element of G. In fact the relations provide a list of strings that can be either introduced where we want, or cancelled out whenever we see them, without changing the 'value', i.e. the group element that is the result of the multiplication.
For a simple example, take the presentation ⟨xy|x3⟩. Writing y for the inverse of x, we have possible strings combining any number of x and y symbols. Whenever we see xxx, or xy or yx we may strike these out. We should also remember to strike out yyy; this says that since the cube of x is the identity element of G, so is the cube of the inverse of x. Under these conditions the word problem becomes easy. First reduce strings to e, x, xx, y or yy. Then note that we may also multiply by xxx, so we can convert yy to x. The result is that we can prove that the word problem here, for what is the cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
of order three, is solvable.
This is not, however, the typical case. For the example, we have a canonical form
Canonical form
Generally, in mathematics, a canonical form of an object is a standard way of presenting that object....
available that reduces any string to one of length at most three, by decreasing the length monotonically. In general, it is not true that one can get a canonical form for the elements, by stepwise cancellation. One may have to use relations to expand a string many-fold, in order eventually to find a cancellation that brings the length right down.
The upshot is, in the worst case, that the relation between strings that says they are equal in G is not decidable
Decidable
The word decidable may refer to:* Decidable language*Decidability for the equivalent in mathematical logic*Gödel's incompleteness theorem, a theorem on the indecidability of languages consisting of "true statements" in mathematical logic....
.
Examples
The following groups have a solvable word problem:- Automatic groupAutomatic groupIn mathematics, an automatic group is a finitely generated group equipped with several finite-state automata. These automata can tell if a given word representation of a group element is in a "canonical form" and can tell if two elements given in canonical words differ by a generator.More...
s, including:- Finite groupFinite groupIn mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
s - Polycyclic groupPolycyclic groupIn mathematics, a polycyclic group is a solvable group that satisfies the maximal condition on subgroups...
s - Negatively curved groups
- Euclidean groupEuclidean groupIn mathematics, the Euclidean group E, sometimes called ISO or similar, is the symmetry group of n-dimensional Euclidean space...
s - Coxeter groupCoxeter groupIn mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
s - Braid groupBraid groupIn mathematics, the braid group on n strands, denoted by Bn, is a group which has an intuitive geometrical representation, and in a sense generalizes the symmetric group Sn. Here, n is a natural number; if n > 1, then Bn is an infinite group...
s - Geometrically finite groups
- Finite group
- Finitely generated recursively absolutely presented groupAbsolute presentation of a groupIn mathematics, one method of defining a group is by an absolute presentation.Recall that to define a group G\ by means of a presentation, one specifies a set S\ of generators so that every element of the group can be written as a product of some of these generators, and a set R\ of relations...
s, including:- Finitely presented simple groups.
- Finitely presented residually finite groups
- One relator groups (this is a theorem of Magnus), including:
- Fundamental groups of closed orientable two-dimensional manifolds.
- Combable groups
Examples with unsolvable word problems are also known:
- Given a recursively enumerable set A of positive integers that has insoluble membership problem, ⟨a,b,c,d | anban = cndcn : n ∈ A⟩ is a finitely generated group with a recursively enumerable presentation whose word problem is insoluble
- Every finitely generated group with a recursively enumerable presentation and insoluble word problem is a subgroup of a finitely presented group with insoluble word problem
- The number of relators in a finitely presented group with insoluble word problem may be as low as 14 by or even 12 by , .
- An explicit example of a reasonable short presentation with insoluble word problem is given in :
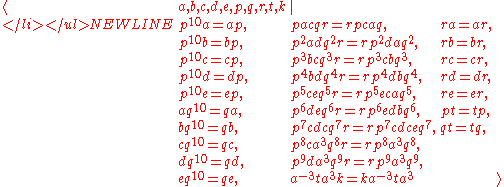
Partial solution of the word problem
The word problem for a recursively presented group can be partially solved in the following sense:
-
- Given a recursive presentation P = ⟨X|R⟩ for a group G, define:
- then there is a partial recursive function fP such that:
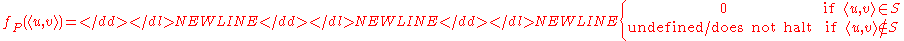
More informally, there is an algorithm that halts if u=v, but does not do so otherwise.
It follows that to solve the word problem for P it is sufficient to construct a recursive function g such that:-

However u=v in G if and only if uv−1=1 in G. It follows that to solve the word problem for P it is sufficient to construct a recursive function h such that:-

Example
The following will be proved as an example of the use of this technique:
-
- Theorem: A finitely presented residually finite group has solvable word problem.
Proof: Suppose G = ⟨H|R⟩ is a finitely presented, residually finite group.
Let S be the group of all permutations of N, the natural numbers, that fixes all but finitely many numbers then:- S is locally finiteLocally finite groupIn mathematics, in the field of group theory, a locally finite group is a type of group that can be studied in ways analogous to a finite group. Sylow subgroups, Carter subgroups, and abelian subgroups of locally finite groups have been studied....
and contains a copy of every finite group. - The word problem in S is solvable by calculating products of permutations.
- There is a recursive enumeration of all mappings of the finite set X into S.
- Since G is residually finite, if w is a word in the generators X of G then w ≠ 1 in G if and only of some mapping of X into S induces a homomorphism such that w ≠ 1 in S.
Given these facts, algorithm defined by the following pseudocode:
- For every mapping of X into S
- If every relator in R is satisfied in S
- If w ≠ 1 in S
- return 0
- End if
- If w ≠ 1 in S
- End if
- If every relator in R is satisfied in S
- End for
defines a recursive function h such that:
-

This shows that G has solvable word problem.
Unsolvability of the uniform word problem
The criterion, given above for the solvability of the word problem in a single group can be extended to a criterion for the uniform solvability of the word problem for a class of finitely presented groups by a straightforward argument. The result is:
-
- To solve the uniform word problem for a class K of groups it is sufficient to find a recursive function f(P,w) that takes a finite presentation P for a group G and a word w in the generators of G such that whenever in G ∈ K:

-
- Boone- Rogers Theorem: There is no uniform partial algorithm which solves the word problem in all finitely presented groups with solvable word problem.
In other words the uniform word problem for the class of all finitely presented groups with solvable word problem is unsolvable. This has some interesting consequences. For instance the Higman embedding theorem can be used to construct a group containing an isomorphic copy of every finitely presented group with solvable word problem. It seems natural to ask whether this group can have solvable word problem. But it is a consequence of the Boone-Rogers result that:
-
- Corollary: There is no universal solvable word problem group. That is, if G is a finitely presented group which contains an isomorphic copy of every finitely presented group with solvable word problem, then G itself must have unsolvable word problem.
Remark: Suppose G = ⟨X|R⟩ is a finitely presented group with solvable word problem and H is a finite subset G. Let H* = ⟨H⟩, be the group generated by H. Then the word problem in H* is solvable: given two words h, k in the generators H of H*, write them as words in X and compare them using the solution to the word problem in G. It is easy to think that this demonstrates a uniform solution the word problem for the class K (say) of finitely generated groups that can be embedded in G. If this were the case the non-existence of a universal solvable word problem group would follow easily from Boone-Rogers. However, solution just exhibited for the word problem for groups in K is not uniform. To see this consider a group J = ⟨Y|T⟩ ∈ K, in order to use the above argument to solve the word problem in J, it is first necessary to exhibit a mapping e: Y → G that extends to an embedding e*: J → G. If there were a recursive function that mapped (finitely generated) presentations of groups in K to embeddings into G, then a uniform solution the word problem in K could indeed be constructed. But there is no reason, in general, to suppose that such a recursive function exists. However, it turns out that, using a more sophisicated argument, the word problem in J can be solved without using an embedding e: J → G. Instead an enumeration of homomorphisms is used, and since such enumeration can be constructed uniformly, it results in a uniform solution to the word problem in K.
Proof that there is no universal solvable word problem group
Suppose G were a universal solvable word problem group. Given a finite presentation P = ⟨X|R⟩ of a group H, one can recursively enumeration all homomorphisms h: H → G by first enumerate all mappings h†: X → G. Not all of these mappings extend to homomorphisms, but, since h†(R), is finite, it is possible to distinguish between homomorphism and non-homomorphisms by using the solution to the word problem in G. "Weeding out" non-homomorphisms gives the required recursive enumeration: h1, h2, ..., hn, ... .
If H has solvable word problem, then at least one of these homomorphism must be an embedding. So given a word w in the generators of H:
Consider the algorithm described by the pseudocode:
-
- Let n=0
- Let repeat=TRUE
- while (repeat
TRUE)
FALSE- increase n by 1
- if (solution to word problem in G reveals hn(w) ≠ 1 in G)
- Let repeat
-
- output 0.
This describes a recursive function:
-

The function f clearly depends on the presentation P. Considering it to be a function of the two variables, a recursive function f(P,w) has been constructed that takes a finite presentation P for a group G and a word w in the generators of G such that whenever G has soluble word problem:
-

But this uniformly solves the word problem for the class of all finitely presented groups with solvable word problem contradicting Boone-Rogers. This contradiction proves G cannot exist.
Algebraic structure and the word problem
There are a number of results that relate solvability of the word problem and algebraic structure. The most significant of these is the Boone-Higman theorem:
-
- A finitely presented group has solvable word problem if and only if it can be embedded in a simple groupSimple groupIn mathematics, a simple group is a nontrivial group whose only normal subgroups are the trivial group and the group itself. A group that is not simple can be broken into two smaller groups, a normal subgroup and the quotient group, and the process can be repeated...
that can be embedded in a finitely presented group.
- A finitely presented group has solvable word problem if and only if it can be embedded in a simple group
It is widely believed that it should be possible to do the construction so that the simple group itself is finitely presented. If so one would expect it to be difficult to prove as the mapping from presentations to simple groups would have to be non-recursive.
The following has been proved by Bernhard NeumannBernhard NeumannBernhard Hermann Neumann AC FRS was a German-born British mathematician who was one of the leading figures in group theory, greatly influencing the direction of the subject....
and Angus MacintyreAngus MacIntyreAngus John Macintyre is a British mathematician known for his contributions to Model theory and logic. He is professor of mathematics at the Queen Mary, University of London....
:
-
- A finitely presented group has solvable word problem if and only if it can be embedded in every algebraically closed groupAlgebraically closed groupIn mathematics, in the realm of group theory, a group A\ is algebraically closed if any finite set of equations and inequations that "make sense" in A\ already have a solution in A\...
- A finitely presented group has solvable word problem if and only if it can be embedded in every algebraically closed group
What is remarkable about this is that the algebraically closed groups are so wild that none of them has a recursive presentation.
The oldest result relating algebraic structure to solvability of the word problem is KuznetsovKuznetsovKuznetsov, Kuznyetsov, or Kuznetsoff or Kuznetsova is the third most common Russian surname, an equivalent of the English "Smith" ....
's theorem:
-
- A recursively presented simple group S has solvable word problem.
To prove this let ⟨X|R⟩ be a recursive presentation for S. Choose a ∈ S such that a ≠ 1 in S.
If w is a word on the generators X of S, then let:
There is a recursive function such that:
such that:
-

Write:
Then because the construction of f was uniform, this is a recursive function of two variables.
It follows that: h(w)=g(w, a) is recursive. By construction:
-

Since S is a simple group, its only quotient groups are itself and the trivial group. Since a ≠ 1 in S, we see a = 1 in Sw if and only if Sw is trivial if and only if w ≠ 1 in S. Therefore:
-

The existence of such a function is sufficient to prove the word problem is solvable for S.
This proof does not prove the existence of a uniform algorithm for solving the word problem for this class of groups. The non-uniformity resides in choosing a non-trivial element of the simple group. There is no reason to suppose that there is a recursive function that maps a presentation of a simple groups to a non-trivial lement of the group. However, in the case of a finitely presented group we know that not all the generators can be trivial (Any individual generator could be, of course). Using this fact it is possible to modify the proof to show:
- The word problem is uniformly solvable for the class of finitely presented simple groups.
-
-
-
-
- To solve the uniform word problem for a class K of groups it is sufficient to find a recursive function f(P,w) that takes a finite presentation P for a group G and a word w in the generators of G such that whenever in G ∈ K:
-
-
-
-
- Given a recursive presentation P = ⟨X|R⟩ for a group G, define:
-